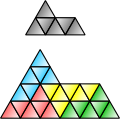
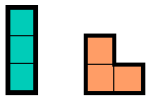In the geometry of tessellations, a rep-tile or reptile is a shape that can be dissected into smaller copies of the same shape. The term was coined as...

aperiodic tilings. One class that can be generated in this way is the rep-tiles; these tilings have unexpected self-replicating properties. Pinwheel tilings are...

composed of n identical pieces is the same thing as a 'self-replicating tile' or rep-tile, of which setisets are therefore a generalization. Setisets using...

non-periodic tiling of the plane. The sphinx is therefore a rep-tile (a self-replicating tessellation). It is one of few known pentagonal rep-tiles and is the...

is, they are rep-tiles. Continuing this dissection recursively leads to a tiling of the plane, which in many cases is an aperiodic tiling. In this context...

coined the term rep-tiles for self-replicating tilings. In 2012, Lee Sallows identified rep-tiles as a special instance of a self-tiling tile set or setiset...

frequent. Several polyominoes can tile larger copies of themselves, and repeating this process recursively gives a rep-tile tiling of the plane. For instance...

is rep-tiled into pieces each scaled down by a scale-factor of 1/r, there are a total of rn pieces. Now, consider the Koch curve. It can be rep-tiled into...

types of tiling are possible. An example is the sphinx tiling, an aperiodic tiling formed by a pentagonal rep-tile. The sphinx may also tile the plane...

surrounding one larger copy at the center. Hence, it is an irrep-7 irrep-tile (see Rep-tile for discussion). The fractal dimension of the Koch curve is ln ⁡ 4...