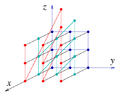
Lie theory and related areas of mathematics, a lattice in a locally compact group is a discrete subgroup with the property that the quotient space has...
31 KB (4,840 words) - 06:28, 11 August 2024
a discrete subgroup of PSL(2,R). The modular group is a lattice in PSL(2,R), but it is not cocompact. Kleinian groups are, by definition, discrete subgroups...
7 KB (899 words) - 11:34, 23 October 2024
points Lattice (discrete subgroup), a discrete subgroup of a topological group whose quotient carries an invariant finite Borel measure Lattice (module)...
2 KB (333 words) - 08:55, 23 November 2023
some maximum distance of a lattice point. Closure under addition and subtraction means that a lattice must be a subgroup of the additive group of the...
17 KB (2,269 words) - 03:56, 30 July 2024
Congruence relation Equivalence class Equivalence relation Lattice (group) Lattice (discrete subgroup) Multiplication table Prime number Up to Abelian variety...
10 KB (800 words) - 23:24, 17 September 2024
but the rational numbers, Q, do not. A lattice in a locally compact topological group is a discrete subgroup with the property that the quotient space...
15 KB (1,575 words) - 05:36, 16 October 2024
List of Lie groups topics (section Discrete groups)
derivative Darboux derivative Lie groupoid Lie algebroid Lattice (group) Lattice (discrete subgroup) Frieze group Wallpaper group Space group Crystallographic...
4 KB (360 words) - 19:55, 10 January 2024
Arithmetic group (redirect from Arithmetic subgroup)
arithmetic lattice in S L n ( R ) {\displaystyle \mathrm {SL} _{n}(\mathbb {R} )} . A lattice in a Lie group is usually defined as a discrete subgroup with...
22 KB (3,301 words) - 18:38, 18 September 2024
In abstract algebra, a normal subgroup (also known as an invariant subgroup or self-conjugate subgroup) is a subgroup that is invariant under conjugation...
19 KB (3,157 words) - 18:44, 15 December 2024
have infinite order. The subgroups of any given group form a complete lattice under inclusion, called the lattice of subgroups. (While the infimum here...
20 KB (1,643 words) - 00:28, 16 December 2024