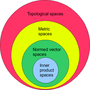
In mathematics, a topological vector space (also called a linear topological space and commonly abbreviated TVS or t.v.s.) is one of the basic structures...

convex topological vector spaces (LCTVS) or locally convex spaces are examples of topological vector spaces (TVS) that generalize normed spaces. They can...

Fréchet spaces, named after Maurice Fréchet, are special topological vector spaces. They are generalizations of Banach spaces (normed vector spaces that...

put it more abstractly every seminormed vector space is a topological vector space and thus carries a topological structure which is induced by the semi-norm...

analysis and related areas of mathematics, a complete topological vector space is a topological vector space (TVS) with the property that whenever points get...

be called the algebraic dual space. When defined for a topological vector space, there is a subspace of the dual space, corresponding to continuous linear...

mathematics, a set in a topological vector space is called bounded or von Neumann bounded, if every neighborhood of the zero vector can be inflated to include...

is a compact complete set that is not closed. Any topological vector space is an abelian topological group under addition, so the above conditions apply...

the case of topological vector spaces, which include function spaces, inner product spaces, normed spaces, Hilbert spaces and Banach spaces. In this article...

pseudometrizable) topological vector space (TVS) is a TVS whose topology is induced by a metric (resp. pseudometric). An LM-space is an inductive limit...