transformées de Fourier. Applications. Mathematical Society of Japan. Mandelbrojt, Szolem (1972) [1969]. Dirichlet series. Principles and methods [Séries de Dirichlet...

this continuation observes that the series for the zeta function and the Dirichlet eta function satisfy the relation ( 1 − 2 2 s ) ζ ( s ) = η ( s ) = ∑...

Linnik's theorem in analytic number theory answers a natural question after Dirichlet's theorem on arithmetic progressions. It asserts that there exist positive...

Kolmogorov, "Une série de Fourier–Lebesgue divergente presque partout", Fundamenta Mathematicae 4 (1923), 324–328. Andrey Kolmogorov, "Une série de Fourier–Lebesgue...

modular forms or automorphic forms. The Riemann zeta function and the Dirichlet L-function satisfy the Euler product, and due to their completely multiplicative...

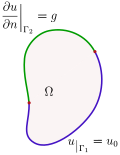
a mixed boundary value problem, the solution is required to satisfy a Dirichlet or a Neumann boundary condition in a mutually exclusive way on disjoint...

(5): 279–281. doi:10.2307/3029800. JSTOR 3029800. Dirichlet PGL (1832). "Démonstration du théorème de Fermat pour le cas des 14e puissances". Journal für...

also arises as the Euler-Lagrange equation of a functional called the Dirichlet energy. As such, the theory of harmonic maps contains both the theory...

(5): 279–281. doi:10.2307/3029800. JSTOR 3029800. Dirichlet PGL (1832). "Démonstration du théorème de Fermat pour le cas des 14e puissances". J. Reine...

polylogarithm function is defined by a power series in z, which is also a Dirichlet series in s: Li s ⁡ ( z ) = ∑ k = 1 ∞ z k k s = z + z 2 2 s + z 3 3 s...