Festigkeitslehre – Wikipedia

Die Festigkeitslehre ist ein Teilgebiet der technischen Mechanik. Ihre Hauptanwendungsgebiete sind Bauwesen (Baustatik) und Maschinenbau. Mit ihren Gesetzen wird untersucht, ob Bauwerke oder Maschinen die ihnen auferlegten Belastungen ertragen, d. h. nicht zu Bruch gehen oder sich nicht übermäßig verformen. Wegen des Einbezugs der Verformung wird oft der erweiterte Begriff Festigkeits- und Verformungslehre gebraucht.

Mit ihrer Hilfe werden die bei Belastung im Körper entstehenden Spannungen und die am Körper auftretenden Verformungen mit den zulässigen Werten verglichen. Die zulässigen Spannungen sind im Wesentlichen vom verwendeten Werkstoff und die zulässigen Verformungen vom Gebrauch der Bauteile vorgegeben.

Handelt es sich um elastische Verformungen, so wird neben Festigkeitslehre auch der Begriff Elastostatik gebraucht. Plastische Verformungen sind Gegenstand der Plastizitätstheorie.^[1]

Im Altertum und im Mittelalter bestimmten die Baumeister nach Tradition, Erfahrung und Intuition, welche Festigkeit Bauwerke und Maschinen haben sollten, damit sie weder versagten noch überdimensioniert wurden. Erste konkrete Versuche, wie sich unterschiedliche Materialien unter Einwirkung von Last verhalten, wurden von Galileo Galilei zu Beginn des 17. Jahrhunderts durchgeführt.^[1] Systematische und verlässliche Ergebnisse wurden ab etwa 1800 insbesondere von Claude Louis Marie Henri Navier, Adhémar Jean Claude Barré de Saint-Venant, Gabriel Lamé, Siméon Denis Poisson und Christian Otto Mohr erzielt. Die Namen dieser Wissenschaftler finden sich noch heute in nach ihnen benannten Begriffen der Festigkeitslehre wieder. Das Fachgebiet der Festigkeitslehre umfasst große Teile der Elastizitäts- und der Plastizitätstheorie,^[1] sowie das Kriechen (Viskosität) von Feststoffen. Die Festigkeitslehre findet heute insbesondere bei Berechnungen im Bauwesen sowie im Maschinenbau Anwendung.

Mechanische Spannung (kurz: Spannung) und Verzerrung sind die beiden grundlegenden Größen der Festigkeitslehre. Die Festigkeitslehre beschäftigt sich hauptsächlich auf der Mikro- und Makroebene, wo in der Kontinuumsmechanik, streng genommen nur Spannungen vorliegen. Diese Spannungen werden auf Querschnittsebene zu resultierenden Kräften und Momente zusammengefasst, und interagiert hier mit der Baustatik. Die Festigkeitslehre beschäftigt sich auch damit, welche Spannungen im Querschnitt die Spannungsresultanten – diese werden in der Theorie I. Ordnung in der Baustatik mit den Schnittgrößen gleichgesetzt – hervorrufen. Hier sind insbesondere folgende Resultanten für die Baustatik interessant: Normalkraft ${\displaystyle N}$, Querkraft ${\displaystyle V}$, Biegemomente ${\displaystyle M}$ und Torsionsmoment ${\displaystyle T}$. Die Verteilung dieser Belastungen im Inneren des Körpers wird durch die Spannung wiedergegeben.^[1] Der elementare Spannungsbegriff, Spannung gleich Kraft pro Fläche, wurde von Augustin-Louis Cauchy im Jahr 1822 geprägt.^[2]

Durch Normalkräfte oder Kraftkomponenten orthogonal zur betrachteten Fläche wird die Normalspannung ${\displaystyle N=\int \sigma _{xx}\,\mathrm {d} A}$ eingeleitet. Somit folgt, dass die mittlere Spannung in Längsrichtung ${\displaystyle \langle \sigma _{xx}\rangle ={\tfrac {N}{A}}}$ die Normalkraft je Querschnittsfläche ist.

Das Biegemoment hängt ebenso von den Spannungen in Längsrichtung ab: ${\displaystyle M_{y}=\int \sigma _{xx}\cdot z\ \mathrm {d} A}$.

Querkräfte ${\displaystyle V_{z}=\int \tau _{xz}\,\mathrm {d} A}$ werden durch Schubspannung von Querschnitten aufgenommen. Bei Rechtecksquerschnitten mit einer Höhe h (in z-Richtung) und der x-Achse im Schwerpunkt, die in Hauptträgheitsachsen beansprucht werden, ist zu beachten, dass die Schubspannungen ${\displaystyle \tau _{xz}}$ in der Elastizitätstheorie einen quadratischen Verlauf über den Querschnitt haben, da an der freien Oberfläche (im Allgemeinen) für die Schubspannungen ${\displaystyle \tau _{zx}=0}$ gilt und aufgrund der Symmetrie des Spannungstensors folgt, dass die Schubspannungen ${\displaystyle \tau _{xz}=0}$ für ${\displaystyle z=\pm h/2}$ Null sind.

Die obenstehenden Gleichungen, reichen nicht aus, um einen Querschnitt eindeutig zu bemessen, es gibt unendlich viele Querschnittkennwertkominationen (z. B. ${\displaystyle A,S_{y}}$). Des Weiteren sind auch Spannungkomponenten-Interaktionen auf Werkstoffebene (z. B. Vergleichsspannung) zu berücksichtigen; und man muss im Allgemeinen (sowohl in der Elastizitätstheorie, als auch in der Plastizitätstheorie) für jede Faser des Werkstoffs nachweisen, dass bestimmte Festigkeitskriterien eingehalten werden.

Die Spannung ist genau genommen eine tensorielle Größe, sie wird um das zu verdeutlichen Spannungstensor genannt: ${\displaystyle \mathbf {\sigma } ={\begin{bmatrix}\sigma _{xx}&\tau _{xy}&\tau _{xz}\\\tau _{yx}&\sigma _{yy}&\tau _{yz}\\\tau _{zx}&\tau _{zy}&\sigma _{zz}\end{bmatrix}}}$

Auf der Hauptdiagonalen finden sich drei Normalspannungen. Die Spur des Spannungstensors ist vom Koordinatensystem Invariant. Die übrigen Elemente repräsentieren die Schubspannungen. Aufgrund der Symmetrie des Spannungstensors gibt es drei voneinander unabhängige Schubspannungen.^[2] Durch Hauptachsentransformation lässt sich jeder Spannungszustand in ein Koordinatensystem umrechnen, in dem alle Schubspannungen verschwinden (Eigenwert-/Eigenvektor-problem).

Ein grafisches Verfahren, um Hauptspannungen, ihre Richtungen und Hauptschubspannungen zu ermitteln, stellt der Mohrsche Spannungskreis dar.

In der Mechanik deformierbarer Körper geht mit jeder Spannung auf einen Körper eine Verzerrung – und somit eine Verformung – dieses Körpers einher. Der elementare Verzerrungsbegriff wird im Allgemeinen^{[Anmerkung 1]} als Verzerrung, d. h. als den Quotienten von Längenänderung zu Ursprungslänge verstanden: ${\displaystyle \varepsilon ={\tfrac {\Delta l}{l}}}$^[2]

Die Verzerrung ist ebenso wie die Spannung eine tensorielle Größe:

Da in der technischen Anwendung die betrachteten Verschiebungsableitungen (also Verzerrungen und Starrkörperrotationen) im Allgemeinen klein gegen 1 sind (${\displaystyle {\tfrac {\delta u_{i}}{X_{j}}}\ll 1}$), ist es üblich, den linearisierten Verzerrungstensor ${\displaystyle \mathbf {\varepsilon } ={\begin{bmatrix}\varepsilon _{xx}&\varepsilon _{xy}&\varepsilon _{xz}\\\varepsilon _{yx}&\varepsilon _{yy}&\varepsilon _{yz}\\\varepsilon _{zx}&\varepsilon _{zy}&\varepsilon _{zz}\end{bmatrix}}}$ anstelle des Green-Lagrange'schen-Verzerrungstensors ${\displaystyle \mathbf {E} ={\begin{bmatrix}E_{xx}&E_{xy}&E_{xz}\\E_{yx}&E_{yy}&E_{yz}\\E_{zx}&E_{zy}&E_{zz}\end{bmatrix}}}$ zu verwenden.

Die Hauptdiagonalelemente des linearen Verzerrungstensors beschreiben die Dehnung ${\displaystyle \varepsilon }$, definiert als die relative Längenänderung eines Linienelements ${\displaystyle \varepsilon _{xx}={\tfrac {\partial u}{\partial X}}}$.^{[Anmerkung 2]} Die übrigen Elemente des Verzerrungstensors beschreiben die Scherung ${\displaystyle \varepsilon }$, definiert als der symmetrische halbe Anteil der Winkeländerung zweier ursprünglich orthogonaler Linienelemente im Schnittpunkt. Die Winkeländerung ${\displaystyle \gamma _{ij}=\varepsilon _{ij}+\varepsilon _{ji}}$^{[Anmerkung 3]} entspricht den doppelten der Schubverzerrungkomponenten im Verzerrungstensor.

Das Spannungs-Dehnungs-Diagramm resultiert oftmals^{[Anmerkung 4]} aus Messdaten (z. B. eines Zugversuches) und stellt einen Zusammenhang zwischen Spannung und Verzerrung her, indem auf der Abszisse die Dehnung und auf der Ordinate die Spannung (i. d. R. die Normalspannung) abgetragen wird. Für duktile Materialien lässt sich der funktionale Zusammenhang oftmals^{[Anmerkung 5]} in einen linear-elastischen Bereich, in einen nichtlinear-elastischen Bereich und in einen plastischen Bereich unterteilen. Für die Festigkeitslehre ist je nach Werkstoff und Anwendung der linear-elastische Bereich ausreichend. Jedoch im Stahlbau, Betonbau sowie im Holzbau wird der elastische Bereich (außer in Sonderfällen) in einer statischen Berechnung verlassen. Im Holzbau und Betonbau werden die Verzerrungen im Allgemeinen linear über den Querschnitt angenommen (Bernoullische Annahmen), jedoch nimmt man bezüglich der Spannungsverteilung im Betonbau gemäß aktueller Normung ein plastisches Plateau (etwa Block-Verteilung oder Parabel-Rechteck-Verteilung) an. Im Stahlbau gibt es in der aktuellen Normung eine Querschnittsklassifizierung, welche festlegt, welche Verfahren zulässig sind,^{[Anmerkung 6]} wobei die im Bauwesen genormten Profile i. d. R. die höchste Klasse (nämlich die Klasse 1) erfüllen. Sie werden aber meistens – auf der sicheren Seite liegend – nur für Klasse 2 (Durchplastifizieren des Querschnittes, aber keine Rotationsfähigkeit angenommen) oder nur für Klasse 3 (elastisch) nachgewiesen.

Im linear-elastischen Bereich beschreibt der Graph eine Gerade; es gilt das verallgemeinerte Hookesche Gesetz ${\displaystyle \sigma =\mathbf {E} \cdot \mathbf {\varepsilon } }$. Hierbei ist ${\displaystyle \mathbf {E} }$ der Elastizitätstensor. Die Elastizitätsmoduln können durch die Ultraschallprüfung bestimmt werden. Elastizitätsmoduln werden auch durch (ein- wie auch mehrachsige) Druck- oder Zugversuche im linear-elastischen Bereich bestimmt. Die Elastizitätsgrößen stellen wichtige Größen für die Auslegung von Körpern in der Festigkeitslehre dar.^[1]

Auf das Spannungs-Dehnungs-Diagramm Bezug nehmend, wird normalerweise die Fließspannung definiert. Versagenskriterien für (ein oder mehrachsige) Festigkeiten werden oft aus dem Spannungs-Dehnungs-Diagramm definiert. Diese Festigkeiten finden Anwendung bei der Wahl des Werkstoffs für gegebene Anwendungen. So wird im Bauwesen häufig Stahlbeton eingesetzt, wobei hier in der statischen Berechnung i. d. R. dem Stahl ausschließlich Zugspannungen und dem Beton ausschließlich Druckspannungen zugeordnet werden.

Das Schubspannungs-Scherungs-Diagramm resultiert oftmals aus den Messdaten der Beanspruchung einer Probe auf Schub. Im Schubspannungs-Scherungs-Diagramm wird auf der Abszisse die Scherung und auf der Ordinate die Schubspannung abgetragen. Im linear-elastischen Bereich verläuft der Graph des Schubspannungs-Scherungs-Diagramms linear. In der Festigkeitslehre gilt, im linear elastischen Bereich: ${\displaystyle \tau =G\gamma }$. Die Proportionalitätskonstante ist der Schubmodul ${\displaystyle G}$.

Bei steigender Temperatur dehnt sich ein Werkstoff meist aus (Wärmedehnung), bei sinkender Temperatur zieht er sich zusammen. Dieser Zusammenhang lässt sich linearisieren und durch folgende Gleichungen modellieren:

${\displaystyle \mathbf {\varepsilon _{T}} =\Delta T\cdot \alpha }$

und

${\displaystyle \Delta l=L_{0}\cdot \mathbf {\varepsilon _{T,xx}} }$.

Hierbei ist

• ${\displaystyle \Delta T}$ die Änderung der Temperatur
• ${\displaystyle \alpha }$ der Wärmeausdehnungskoeffizient
• ${\displaystyle \Delta l=l-L_{0}}$ die Längenänderung eines Körpers
• ${\displaystyle L_{0}}$ seine Ursprungslänge.

Wird die Ausdehnung verhindert:

${\displaystyle \mathbf {\varepsilon } =\mathbf {\varepsilon _{T}+\varepsilon _{\sigma }} =0}$,

so folgt, dass die Verzerrung zufolge Spannung (Zwängung) gleich der negativen Tempteraturausdehnung ist:

${\displaystyle \Rightarrow \mathbf {\varepsilon _{\sigma }} =-\mathbf {\varepsilon _{T}} =-\Delta T\cdot \alpha }$.

Die Eigenschaften des Werkstoffs und die Geometrie eines Körpers nimmt Einfluss auf dessen Verhalten bei Belastung. Das Flächenträgheitsmoment ist ein rein geometrisches Maß für die Widerstandsfähigkeit eines Querschnitts durch einen Körper gegen Verformung durch Biegung und Torsion. Unterschieden werden das polare Flächenträgheitsmoment ${\displaystyle I_{p}}$, die axialen Flächenträgheitsmomente ${\displaystyle I_{xx}}$ und ${\displaystyle I_{yy}}$ sowie die Deviationsmomente ${\displaystyle I_{xy}=I_{yx}}$.

Das Flächenträgheitsmoment lässt sich darüber hinaus tensoriell auffassen; es gilt ${\displaystyle \mathbf {J} ={\begin{bmatrix}I_{p}&0&0\\0&I_{yy}&I_{yz}\\0&I_{zy}&I_{zz}\end{bmatrix}}}$.^[2] Der Flächenträgheitstensor wird dabei mit ${\displaystyle \mathbf {J} }$ bezeichnet, da ${\displaystyle \mathbf {I} }$ bereits für die Identität verwendet wird.

Die Eigenwerte des Flächenträgheitstensors sind die Maxima des axialen Flächenträgheitsmoments in einem Schwerpunktsystem und werden Hauptträgheitsmomente genannt.^[2] Zur Bestimmung der Hauptträgheitsmomente können Transformationsbeziehungen verwendet werden.

Um die Flächenträgheitsmomente aufwändiger Querschnittsflächen einfacher berechnen zu können, kann eine Zerlegung in Teilflächen und die Berechnung der Flächenträgheitsmomente dieser Teilflächen erfolgen. Stimmt der Schwerpunkt einer Teilfläche dabei nicht mit dem Gesamtschwerpunkt überein, ist nach dem Steinerschen Satz zu den axialen Flächenträgheitsmomente und den Deviationsmomenten der Steiner-Anteil hinzuzufügen.^[2]

Das Flächenträgheitsmoment hat eine große praktische Bedeutung, denn mit dessen Kenntnis lassen sich Bauteile bei gegebener Hauptlastrichtung und gegebenem Materialeinsatz möglichst widerstandsfähig gestalten. Dies ist der Grund für den häufigen Einsatz von Profilstählen, wie etwa dem Doppel-T-Träger, anstelle von Vollmaterial.

Den Betrachtungen der Statik (z. B. Baustatik) oder der Dynamik (z. B. Baudynamik) folgend, werden, Bezug nehmend auf eine durch einen elastischen Stab hindurchgelegte Linie, demselben Beanspruchungen zugeordnet. Welche Spannungen aus solchen Beanspruchungen im Querschnitt resultieren, ist Gegenstand der Festigkeitslehre.

Ein elementarer Bestandteil der Festigkeitslehre sind Aussagen über Spannungen und Deformationen an Körpern durch Biegung. Hierbei wird in der Balkentheorie das Modell des Balkens verwendet, da sich eine Vielzahl an Bauteilen, insbesondere Tragwerkskomponenten und Wellen, als Balken modellieren lassen.

Allgemein wird zwischen der geraden Biegung und der schiefen Biegung unterschieden. Die gerade Biegung erfolgt durch Belastung entlang der Hauptträgheitsachsen eines Balkens; bei achsensymmetrischen Querschnitten sind dies die Symmetrieachsen.

Bei der Biegung eines Balkens durch ein Moment oder eine Belastung, die ein Biegemoment erzeugt, tritt in dem Balken eine Normalspannung auf. Da die untersuchten Balken meistens lang im Verhältnis zur Dicke (schlanker Balken) und die Durchbiegungen relativ gering sind, wird oft^{[Anmerkung 7]} angenommen, dass die Biegenormalspannung sich über den Querschnitt linear ändert (siehe Bild rechts). Bei gerader Biegung ist die Biegenormalspannung nur von einer Hauptträgheitsachse abhängig. Die betragsmäßig größten Biegenormalspannungen treten an jener Faser des Balken auf die den größten oder kleinsten Wert auf dieser Hauptträgheitsachse hat. Wenn keine Normalkraft vorliegt, geht der Nulldurchgang der Spannung (die Nulllinie oder die neutrale Faser) durch den Schwerpunkt des Querschnitts. In diesem Fall hängt bei gerader Biegung das Vorzeichen der Spannung nur vom Vorzeichen der Hauptträgheitsachse ab, sofern die Stablängsachse im Schwerpunkt liegt.

Die Biegespannung bei Biegung kann bei linearer Elastizität unter Annahme der Bernoulli-Balkentheorie folgendermaßen bestimmt werden:

• ${\displaystyle \sigma _{xx}(x,y,z)={\frac {N(x)}{A(x)}}-{\frac {M_{z}(x)\cdot I_{yy}(x)+M_{y}(x)\cdot I_{yz}(x)}{I_{yy}(x)\cdot I_{zz}(x)-I_{yz}^{2}(x)}}\cdot y+{\frac {M_{y}(x)\cdot I_{zz}(x)+M_{z}(x)\cdot I_{yz}(x)}{I_{yy}(x)\cdot I_{zz}(x)-I_{yz}^{2}(x)}}\cdot z.}$^[3]

Dabei sind, bei Beanspruchung in Hauptträgheitsachsen die Spannungsanteile ${\displaystyle {\frac {M_{y}(x)\cdot z}{I_{yy}(x)}}-{\frac {M_{z}(x)\cdot y}{I_{zz}(x)}}}$ Biegespannungen (Eine Art von Normalspannungen) in Abhängigkeit von ${\displaystyle x}$,${\displaystyle y}$ und ${\displaystyle z}$, ${\displaystyle z}$ der Abstand zur x-Achse (Stablängsachse), ${\displaystyle M_{y}}$ das belastende Biegemoment um die y-Achse und ${\displaystyle I_{yy}}$ das axiale Flächenträgheitsmoment. Steht ein Balken zusätzlich zur Belastung durch ein Biegemoment unter einer durch Temperaturänderung durch behinderte (oder verhinderte) Dehnung verursachten Normalspannung (Zwängung), kann die resultierende Normalspannung in der linearen Elastizitätstheorie nach dem Superpositionsprinzip durch Addition der durch Biegemoment verursachten Normalspannung zur thermisch bedingten Normalspannung bestimmt werden. Für die Dimensionierung realer Balken sind in der linearen Elastizitätstheorie oftmals die Randspannungen ausschlaggebend, da bei ausschließlich Biege-Normalkraft-Torsions-Beanspruchungen die Beanspruchung^{[Anmerkung 8]} im übrigen Teil des Balkens stets gleich^{[Anmerkung 9]} oder geringer ist als die Beanspruchung an den Rändern. Bei M-N-V-Interaktion, muss jede Faser nachgewiesen werden, insbesondere im Schwerpunkt, da dort die betragsmäßig größten Schubspannungen vorliegen. Um eine Materialoptimierung (größerer Hebelsarm) zu haben, werden können Querschnitte mit (ev. kontinuierlich) abgestuften Materialfestigkeiten oder Materialbreiten hergestellt werden, oder setzt wie im Stahlbetonbau Materialverbunde ein.^{[Anmerkung 10]} Setzt man die Ränder des Balkens in die Biegespannungsformel ein, ergibt sich bei ausschließlich einachsiger Hauptachsenbiegung in z-Richtung:

• ${\displaystyle \sigma _{xx}(x,y,z)={\frac {M_{y}(x)\cdot z_{\text{Rand}}(x)}{I_{yy}(x)}}}$

Da sowohl ${\displaystyle I_{yy}(x)}$ als auch ${\displaystyle z_{\text{Rand}}(x)}$ geometrische Größen, die nur von der x-Koordinate abhängt, sind, die Biegenormalspannungen, für einen gegebenen Querschnitt, für eine Bestimmte Beanspruchung und linearer Elastizität, eindeutig bestimmbar sind, und können zum Widerstandsmoment ${\displaystyle W}$ zusammengefasst werden.

Es gilt ${\displaystyle \textstyle W_{u}(x)={\frac {I_{yy}(x)}{z_{u}(x)}},\textstyle W_{o}(x)={\frac {I_{yy}(x)}{z_{o}(x)}}}$^{[Anmerkung 11]} und somit ${\displaystyle \textstyle \sigma _{xx}(x,y,z_{u})=\sigma _{xx}(x,z_{u})={\frac {M_{y}(x)}{W_{u}(x)}}}$.

Das Widerstandsmoment ist ebenfalls eine rein geometrische Größe und wird oft bei der Dimensionierung von Balken verwendet, da hierbei durch die Wahl des Werkstoffs gegebene Maximalspannungen nicht überschritten werden dürfen und das Widerstandsmoment einen einfachen Zusammenhang zwischen Biegenormalspannung und der Beanspruchung durch ein Biegemoment herstellt.^[2]

Ein Biegestab (z. B. Träger auf zwei Stützen oder ein Kragarm) wird bei üblichen Koordinatensystem durch ein positives Moment um die positive y-Achse an der Seite mit positiver z-Koordinate mit einer positiven Dehnung beansprucht. Lediglich die Nulllinienebene, in der keine Spannungen vorliegen, die bei ausschließlicher Biegemomentenbeanspruchung durch den Schwerpunkt des Balkenquerschnitts verläuft, bleibt in der Bernoulli-Balkentheorie normalspannungsfrei und behält (bei konstanter Temperatur) somit ihre Länge bei. Da für lange Balken die Bernoullischen Annahmen in guter Näherung gelten, bleibt jede Querschnittsfläche entlang des Balkens eben und orthogonal zur Balkenachse.^[1]

Die Biegelinie bezeichnet die Durchbiegung der Stabachse eines Balkens an einer beliebigen x-Koordinate. Sie besteht im Allgemeinen aus elastischen, plastischen sowie viskosen Anteilen. Die Biegelinie kann in der linearen Elastizitätstheorie über Differenzialbeziehungen durch mehrfache Integration aus Biegemomentverlauf, Querkraftverlauf oder Linienlast gewonnen werden, sofern sie an eindeutig an die Randbediungen anspassbar ist. Es gilt bei über den Querschnitt konstanter Temperatur und bei (einachsiger) Hauptachsenbiegung:^{[Anmerkung 12]}

• ${\displaystyle EI_{y}w_{z}''''=q_{z}(x)}$
• ${\displaystyle EI_{y}w_{z}'''=-Q_{z}(x)}$
• ${\displaystyle EI_{y}w_{z}''=-M_{y}(x)}$.

Dabei ist ${\displaystyle E}$ der Elastizitätsmodul, ${\displaystyle I_{y}}$ das axiale Flächenträgheitsmoment in z-Richtung und ${\displaystyle w_{z}}$ die Durchbiegungkomponente in z-Richtung. Die Integrationskonstanten können ausschließlich bei statisch bestimmten und statisch überbestimmten Systemen eindeutig über die Lagerung des Balkens bestimmt werden.^[2]

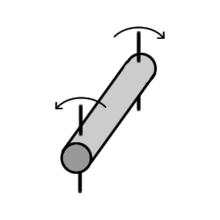
Wird ein Stab durch ein Torsionsmoment beansprucht, treten in seinem Inneren Torsionsschubspannungen auf, die eine infinitesimale Verschiebung seiner Querschnittsflächenelemente bewirken. Die Bauteilsicherheit gegen Torsionsbeanspruchung ist in den meisten Fällen^{[Anmerkung 13]} in einem Standsicherheitsnachweis nachzuweisen.

Bei der Torsion von kreisförmigen Stäben wie Antriebswellen und Rohren bleiben die Querschnitte eben und kreisförmig und gerade Linien in axialer Richtung gerade. Für die in der Technik auftretenden kleinen Verdrehwinkel bleiben Radius und Länge des Stabes also konstant. Die Torsionsschubspannung ${\displaystyle \tau }$ steigt in der linearen Elastizitätstheorie linear mit dem Radius ${\displaystyle r}$ an und ist vom Torsionsmoment ${\displaystyle T}$ und dem polaren Flächenträgheitsmoment ${\displaystyle I_{p}}$ abhängig. Sie berechnet sich mit der Torsionsformel

• ${\displaystyle \tau ={\frac {T\cdot r}{I_{p}}}}$.^[1]

Folglich ist die Torsionsschubspannung auf der Oberfläche des Stabes am größten und über die gesamte Oberfläche konstant.

Der Verdrehwinkel ${\displaystyle \Phi }$ von Stäben mit kreisförmigem Querschnitt wird über folgende Formel berechnet:

• ${\displaystyle \Phi ={\frac {T\cdot l}{I_{p}\cdot G}}}$

Dabei ist ${\displaystyle l}$ die Länge des Stabes und G der Schubmodul.

Bei Wellen, die mehrere Absätze unterschiedlichen Durchmessers besitzen, kann der Gesamtverdrehwinkel berechnet werden, indem für jeden Wellenabsatz die obenstehende Formel angewandt und die Ergebnisse addiert werden.^[1]

Während bei Körpern mit kreisförmigem Querschnitt die Querschnitte unter Torsionsbelastung stets kreisförmig bleiben, tritt bei prismatischen Querschnitten Verwölbung auf, die zu einem komplexen Verdrehungsmuster führt, welches nicht mit einfachen analytischen Mitteln bestimmt werden kann. Bei der Auslegung von prismatischen Stäben auf Torsion wird daher oftmals auf Tabellenwerke zurückgegriffen.

Bei drei- oder viereckigen Querschnitten treten die maximalen Schubspannungen stets an den Mittelpunkten der Seitenflächen auf (siehe Abbildung rechts), während die Ecken aufgrund der Spannungsrandbedingungen spannungsfrei sein müssen.

Da die maximale Schubspannung von kreisförmigen Querschnitten an ihren Rändern auftritt, können dünnwandige Querschnitte Anwendung finden, beispielsweise in Rohren oder Hohlwellen.

Die maximale Schubspannung ${\displaystyle \tau _{\text{max}}}$ an einem dünnwandigen Querschnitt kann bestimmt werden durch ${\displaystyle \tau _{\text{max}}={\frac {T\cdot t}{I_{T}}}}$ mit dem Torsionsträgheitsmoment ${\displaystyle I_{T}}$ und der Wandstärke ${\displaystyle t}$.

Fasst man Torsionsmoment und Wandstärke zum Torsionswiderstandsmoment ${\displaystyle W_{p}}$ zusammen, gilt ${\displaystyle \tau _{\mathrm {max} }={\frac {T}{W_{p}}}}$.^[2]

Der Verdrehwinkel ${\displaystyle \Phi }$ wird berechnet durch ${\displaystyle \Phi ={\frac {Tl}{4A_{0}^{2}G}}\oint {\frac {1}{t}}ds}$.^[1]

Bei dünnwandigen Querschnitten tritt Schubfluss auf, der durch folgende mithilfe der Bredtschen Formel hergeleitete Beziehung bestimmt wird:

• ${\displaystyle q_{T}={\frac {T}{2A_{m}}}}$

Dabei ist ${\displaystyle q_{T}}$ der Schubfluss und ${\displaystyle A_{m}}$ die von der Profilmittellinie eingeschlossenen Fläche. Der Schubfluss ist der Grund für die deutlich höhere Widerstandsfähigkeit von geschlossenen Profilen gegenüber geschlitzten Profilen.^[2]

Sehr schlanke Stäbe neigen zu einem schlagartigen Versagen durch seitliche Auslenkung, sobald man sich einer kritischen Last – zu Ehren Leonhard Eulers auch Euler’sche Knicklast ${\displaystyle P_{\mathrm {kr} }}$ genannt – annähert. Dieser Effekt wird als "Knicken" bezeichnet und ist im Tragsicherheitsnachweis nachzuweisen. Für die Auslegung reicht es i. d. R. nicht aus, dass die kritische Last einfach nur unterhalb der rechnerisch bestimmbaren ("theoretischen") Belastbarkeit eines Stabes gehalten wird, da durch werkstoffliche oder konstruktive Unvollkommenheiten ein Knicken schon vor Erreichen der idealen Knickdruckkraft eintreten kann. Die kritische Last eines Einzelstabes, der ausschließlich auf Normalkraft beansprucht wird, wird bestimmt durch:

• ${\displaystyle P_{\mathrm {kr} }={\frac {\pi ^{2}EI}{(\beta \cdot L)^{2}}}}$^[4]

Hierbei ist ${\displaystyle E}$ der Elastizitätsmodul, ${\displaystyle I}$ das Flächenträgheitsmoment^{[Anmerkung 14]} des Querschnitts, ${\displaystyle L}$ die Länge des Stabs und ${\displaystyle \beta }$ ein Längenfaktor, der abhängig von den Randbediungen (in Sonderfällen eines der Euler-Fälle) (siehe Bild rechts, von links nach rechts) ist. Die Knicklänge ${\displaystyle s_{k}}$ ist der (eventuell virtuelle) Abstand zweier Wendepunkte (Momentennullpunkte) der (eventuell verlängerten) Biegelinie dieses Einzelstabes. Bei Rahmen, als auch drehbar gelagerten Stäben (tritt in der Realität in einer guten Näherung fast immer auf) werden häufig Knicklängendiagramme verwendet.

Durch seine Verformung nimmt ein Körper Energie, die Formänderungsenergie ${\displaystyle W}$, auf. Für Normal- und Schubspannungen innerhalb eines Körpers wird die Formänderungsenergie bestimmt durch

• ${\displaystyle W=\int _{t}\int _{V}{\mathbf {\sigma } \cdot \mathbf {\dot {\varepsilon }} }dVdt}$

Dabei ist:

${\displaystyle \mathbf {\sigma } }$ der Spannungstensor

${\displaystyle \mathbf {\dot {\varepsilon }} }$ der Verzerrungsratentensor

${\displaystyle V}$ das Volumen des betrachteten Körpers

${\displaystyle t}$ die Zeit.

Für Stäbe und Balken lässt sich die Formänderungsenergie abhängig von den auftretenden Belastungen ausdrücken. Dabei ist ${\displaystyle l}$ die Länge des Körpers und ${\displaystyle x}$ die Laufkoordinate in Richtung der Stab- oder Balkenachse.

Die Formänderungsenergie ist in der linearen Elastizitätstheorie für Belastung durch…

• Normalkraft: ${\displaystyle W_{N}=\int _{0}^{l}{\frac {N^{2}}{2EA}}dx}$ mit der Normalkraft ${\displaystyle N}$ und der Querschnittsfläche ${\displaystyle A}$.

• Biegemoment: ${\displaystyle W_{B}=\int _{0}^{l}{\frac {M^{2}}{2EI}}dx}$ mit dem Biegemoment ${\displaystyle M}$ und dem axialen Flächenträgheitsmoment ${\displaystyle I}$ in Richtung der Balkenachse.

• Querkraftschub: ${\displaystyle W_{V}=\int _{0}^{l}{\frac {\chi _{s}Q^{2}}{2GA}}dx}$ mit der Querkraft ${\displaystyle Q}$ und dem Formfaktor ${\displaystyle \chi _{s}={\frac {A}{I}}\int _{A}{\frac {S^{2}}{t^{2}}}dA}$, in dem das statische Moment ${\displaystyle S}$ und die Breite beziehungsweise Wandstärke ${\displaystyle t}$ enthalten sind.

• Torsion: ${\displaystyle W_{T}=\int _{0}^{l}{\frac {M_{T}^{2}}{2GI_{P}}}dx}$ mit Torsionsmoment ${\displaystyle M_{T}}$ und polarem Flächenträgheitsmoment ${\displaystyle I_{P}}$.^[1]

Bei kombinierter Belastung durch mehrere dieser Belastungsarten kann die resultierende Formänderungsenergie durch Addition der einzelnen Formänderungsenergien bestimmt werden.^[2]

Siehe auch: Verformungsenergie, Spannenergie

Mithilfe der Formänderungsenergie und unterschiedlichen Sätzen Energiemethoden lassen sich Aussagen zum Verhalten eines Körpers unter Lasteinwirkung treffen.

• Der Satz von Castigliano besagt, dass die partielle Ableitung der in einem linear-elastischen Körper gespeicherten Formänderungsenergie nach der äußeren Kraft die Verschiebung des Kraftangriffspunkts in Richtung dieser Kraft ergibt.

• Der Satz von Menabrea besagt, dass die partielle Ableitung der Formänderungsenergie nach einer statisch unbestimmten Lagerreaktion gleich Null ist.

• Der Satz von Betti behandelt einen Körper, an dem zwei voneinander unabhängige Kräfte angreifen, und stellt einen Zusammenhang zwischen der Arbeit her, die diese Kräfte auf dem Verschiebungsweg der jeweils anderen Kraft verrichten.^[2]

• Das Prinzip der virtuellen Kräfte wird Johann I Bernoulli zugeschrieben, ist eine Abwandlung des Prinzips der virtuellen Arbeit und ermöglicht die Ermittlung von Verschiebungen und Winkeländerungen an Orten, an denen keine Kraft am Körper angreift. Dazu wird am gewünschten Ort eine virtuelle Kraft eingeführt, die einen beliebigen von Null verschiedenen Wert hat.

Bei Bauteilen von Maschinen oder Elementen eines Gebäudes treten Ungenauigkeiten auf, diese sollten innerhalb der dafür vorgesehenen Toleranzen liegen. Zum einen können Fertigungsfehler die Belastbarkeit reduzieren, die ein Bauteil aufnehmen kann, des Weiteren können Lastannahmen falsch getroffen werden und die tatsächliche Belastung eines Teils über der angenommenen Belastung liegen. Sämtliche kommerzielle Werkstoffe (insbesondere Holz oder Beton) weisen Schwankungen in ihrer Festigkeit auf, die zu berücksichtigen sind. Das Teilsicherheitskonzept des Eurocodes beschreibt eine Möglichkeit dies zu berücksichtigen, wobei ${\displaystyle R_{k}}$ der charakteristische Widerstand (Resistance) und ${\displaystyle E_{k}}$ für die charakteristische Einwirkung steht:

• ${\displaystyle {\frac {R_{k}}{\gamma _{R}}}\geq E_{k}\cdot \gamma _{E}}$

Wobei ${\displaystyle R_{k}}$ und ${\displaystyle E_{k}}$ nicht nur Spannungen oder Verzerrungen, sondern auch Drehwinkel, Temperatur oder ähnliches sein können. Die Versagensbelastung wird im Allgemeinen durch Rechenmodelle (Normen, Computermodelle) ermittelt, die oftmals Daten aus Versuchen oder Gebäudeschäden beinhalten.

Der Sicherheitsfaktor ist dimensionslos, sein Wert ist abhängig von der Sicherheitsrelevanz des zu dimensionierenden Bauteils und der Streuung im Werkstoffverhalten beziehungsweise der Einwirkung zu wählen. Im Hochbau liegt im Betonbau und Holzbau der globale Sicherheitsfaktor im Bereich von 2, in Einzelfällen (Kernkraftwerken) kann (und muss) davon abgewichen werden, außerordentliche Lastfälle (Lastfälle, die nicht zu erwarten sind wie z. B. Autoaufprall) haben einen reduzierten Sicherheitsfaktor auf der Einwirkungs- (=1) als auch auf der Widerstandsseite (tw.=1). Oft sind Sicherheitsfaktoren in Normenwerken zu finden.^[1]

Neben den grundlegenden Größen wie Spannung und Verformung müssen Sicherheiten gegen Langzeitwirkungen wie Korrosion, Kriechen und Ermüdung vorgesehen werden. Kriechen tritt auf, wenn ein Werkstoff über eine lange Zeit, oft unter hohen Temperaturen, eine gleichförmige Belastung erfährt. Ermüdung tritt bei häufigen Belastungswechseln, beispielsweise bei Flugzeugen oder bei Antriebswellen von Fahrzeugen, auf.

• Russel C. Hibbeler: Technische Mechanik 2 Festigkeitslehre. 8. Auflage. Pearson Deutschland, München 2013, ISBN 978-3-86894-126-5.
• Walther Mann: Vorlesungen über Statik und Festigkeitslehre. Überarbeitete und erweiterte Auflage. Teubner, Stuttgart 1997, ISBN 3-519-15238-X.
• Rolf Mahnken: Lehrbuch der Technischen Mechanik – Elastostatik, mit einer Einführung in Hybridstrukturen. Springer, Berlin 2015, ISBN 978-3-662-44797-0.
• Klaus-Dieter Arndt, Holger Brüggemann, Joachim Ihme: Festigkeitslehre für Wirtschaftsingenieure. 2. Auflage. Springer, Berlin/Heidelberg 2014, ISBN 978-3-658-05903-3.
• Bruno Assmann, Peter Selke: Technische Mechanik 2 – Festigkeitslehre. 18. Auflage. Oldenbourg, München 2013, ISBN 978-3-486-70886-8.
• Herbert Balke: Einführung in die Technische Mechanik – Festigkeitslehre. 3. Auflage. Springer, Berlin/Heidelberg 2014, ISBN 978-3-642-40980-6.
• Dietmar Gross, Werner Hauger, Jörg Schröder, Wolfgang Wall: Technische Mechanik 2 – Elastostatik. 10. Auflage. Springer, Berlin/Heidelberg 2009, ISBN 978-3-642-00564-0.
• Günther Holzmann, Heinz Meyer, Georg Schumpich: Technische Mechanik – Festigkeitslehre. 10. Auflage. Springer, Berlin/Heidelberg 2012, ISBN 978-3-8348-0970-4.
• Volker Läpple: Einführung in die Festigkeitslehre. 3. Auflage. Vieweg Teubner, Wiesbaden 2011, ISBN 978-3-8348-1605-4.
• Herbert Mang, Günter Hofstetter: Festigkeitslehre. 4.  Auflage. Springer, Berlin/Heidelberg 2013, ISBN 978-3-642-40751-2 (560 S., springer.com). 
• Otto Wetzell, Wolfgang Krings: Technische Mechanik für Bauingenieure. Band 2: Festigkeitslehre. 3. Auflage. Springer, Berlin/Heidelberg 2015, ISBN 978-3-658-11467-1.
• Karl-Eugen Kurrer: Geschichte der Baustatik. Auf der Suche nach dem Gleichgewicht, Ernst und Sohn, Berlin 2016, S. 380–439, ISBN 978-3-433-03134-6.

1. ↑ Deformation (mechanics) #Strain measures in der englischsprachigen Wikipedia
2. ↑ x=X+u, wobei X die Bezugskonfiguration (i. d. R. undeformiert) und x die Momantanlage(i. d. R. deformierte Lage) ist
3. ↑ Deformation (mechanics) #Shear strain in der englischsprachigen Wikipedia
4. ↑ Mehrachsige Spannung-Dehnungs-Diagramme resultieren oftmals aus Theorien, Annahmen, Normen,… und sind nicht immer messtechnisch bestätigt oder sind z. B. rein fiktiv und liegen auf der sicheren Seite.
5. ↑ Viele Materialien zeigen viskose Eigenschaften.
6. ↑ Klasse 1: Plastisch auf Querschnitts, als auch Systemebene Fließgelenk; Klasse 2: Plastisch auf Querschnitssebene, aber nicht auf Systemebene; Klasse 3: Elastisch; Klasse 4: Aufgrund von lokalen Beulen, elastische Rechnung nicht zulässig.
7. ↑ Annahme gilt nicht im Stahlbau, bei Querschnittsklasse 1 oder 2.
8. ↑ Die Spannungskomponenten können auch negativ und somit kleiner sein.
9. ↑ Das ist der Fall, wenn gilt: My=Mz=T=0.
10. ↑ Der Stahl wird auf der Zugseite eingesetzt (aus Dauerhaftigkeitsgründen mit ausreichender Betondeckung), um einen optimalen Hebelsarm zur Betondruckzohne zu haben.
11. ↑ W_o ist bei üblichen Koordinatensystem negativ.
12. ↑ Dies gilt auch bei veränderlichen Elastizitätsmodul und veränderilchen Flächenträgheitsmoment.
13. ↑ Im Betonbau braucht man i. d. R. nur die Gleichgewichtstorsion, nicht aber die Verträglichkeitstorsion nachweisen.
14. ↑ Bei veränderlichen Flächenträgheitsmoment kann man i. d. R. in einem Traglastnachweis, auf der sicheren Seite liegend, das kleinste Flächenträgheitsmoment annehmen.

Commons: Festigkeitslehre – Sammlung von Bildern, Videos und Audiodateien

1. ↑ ^{a b c d e f g h i j k} Russel C. Hibbeler: Technische Mechanik 2 Festigkeitslehre. 8. Auflage. Pearson Deutschland, München 2013, ISBN 978-3-86894-126-5.
2. ↑ ^{a b c d e f g h i j k l} Bernd Markert: Mechanik 2 Elastostatik – Statik deformierbarer Körper. 2. Auflage. Institut für Allgemeine Mechanik Aachen, Aachen 2015.
3. ↑ Herbert Mang, Günter Hofstetter: Festigkeitslehre. 4. Auflage. Springer, Berlin/Heidelberg 2013, ISBN 978-3-642-40751-2. 
4. ↑ Großübung Stabilität, elastische Knickung, Eulerfälle. (Memento des Originals vom 4. März 2016 im Internet Archive)  Info: Der Archivlink wurde automatisch eingesetzt und noch nicht geprüft. Bitte prüfe Original- und Archivlink gemäß Anleitung und entferne dann diesen Hinweis.@1@2Vorlage:Webachiv/IABot/www.uni-magdeburg.de (PDF) Universität Magdeburg, abgerufen am 10. Oktober 2015.