Das Subdifferential ist eine Verallgemeinerung des Gradienten auf nicht differenzierbare konvexe Funktionen . Das Subdifferential spielt eine wichtige Rolle in der konvexen Analysis sowie der konvexen Optimierung .
Sei f : R n → R {\displaystyle f\colon \mathbb {R} ^{n}\to \mathbb {R} } g ∈ R n {\displaystyle g\in \mathbb {R} ^{n}} Subgradient von f {\displaystyle f} x 0 {\displaystyle x_{0}} x ∈ R n {\displaystyle x\in \mathbb {R} ^{n}} [ 1]
f ( x ) ≥ f ( x 0 ) + ⟨ g , x − x 0 ⟩ {\displaystyle f(x)\geq f(x_{0})+\langle g,x-x_{0}\rangle } wobei ⟨ ⋅ , ⋅ ⟩ {\displaystyle \langle \cdot ,\cdot \rangle } Standardskalarprodukt bezeichnet.
Das Subdifferential ∂ f ( x 0 ) {\displaystyle \partial f(x_{0})} f {\displaystyle f} x 0 {\displaystyle x_{0}} [ 2]
Existieren die folgenden Grenzwerte a = lim x → x 0 − f ( x ) − f ( x 0 ) x − x 0 , {\displaystyle a=\lim _{x\to x_{0}^{-}}{\frac {f(x)-f(x_{0})}{x-x_{0}}},} b = lim x → x 0 + f ( x ) − f ( x 0 ) x − x 0 , {\displaystyle b=\lim _{x\to x_{0}^{+}}{\frac {f(x)-f(x_{0})}{x-x_{0}}},} Intervall [ a , b ] {\displaystyle [a,b]} Subdifferential der Funktion f {\displaystyle f} x 0 {\displaystyle x_{0}} ∂ f ( x 0 ) := [ a , b ] {\displaystyle \partial f(x_{0}):=[a,b]}
Für eine konvexe Funktion gilt a ≤ b {\displaystyle a\leq b} ∂ f ( x 0 ) = ∅ {\displaystyle \partial f(x_{0})=\emptyset }
Subgradienten einer konvexen Funktion Intuitiv bedeutet diese Definition für n = 1 {\displaystyle n=1} f {\displaystyle f} G {\displaystyle G} ( x 0 , f ( x 0 ) ) {\displaystyle (x_{0},f(x_{0}))} g {\displaystyle g}
G = { ( x , y ) ∈ R 2 ∣ y = g ⋅ ( x − x 0 ) + f ( x 0 ) } {\displaystyle G=\{(x,y)\in \mathbb {R} ^{2}\mid y=g\cdot (x-x_{0})+f(x_{0})\}} Da die Normalengleichung von G {\displaystyle G}
− g ⋅ ( x − x 0 ) + 1 ⋅ ( y − f ( x 0 ) ) = 0 {\displaystyle -g\cdot (x-x_{0})+1\cdot (y-f(x_{0}))=0} ist, ist die Normale an G {\displaystyle G} ( − g , 1 ) ∈ R 2 {\displaystyle (-g,1)\in \mathbb {R} ^{2}}
Im allgemeinen Fall n ≥ 1 {\displaystyle n\geq 1} f {\displaystyle f} Hyperebene , die durch den Fußpunkt ( x 0 , f ( x 0 ) ) {\displaystyle (x_{0},f(x_{0}))} ( − g , 1 ) ∈ R n + 1 {\displaystyle (-g,1)\in \mathbb {R} ^{n+1}}
Wegen des Trennungssatzes ist das Subdifferential einer stetigen konvexen Funktion überall nichtleer.
Das Subdifferential der Funktion f : R → R {\displaystyle f\colon \mathbb {R} \rightarrow \mathbb {R} } x ↦ | x | {\displaystyle x\mapsto |x|}
∂ f ( x 0 ) = { { − 1 } x 0 < 0 [ − 1 , 1 ] x 0 = 0 { 1 } x 0 > 0 {\displaystyle \partial f(x_{0})={\begin{cases}\{-1\}&x_{0}<0\\\left[-1,1\right]&x_{0}=0\\\{1\}&x_{0}>0\end{cases}}} Eine ähnliche Eigenschaft ist bei der Lasso-Regression für die Herleitung der Soft-Threshold-Funktion wichtig.
Sei f : R n → R {\displaystyle f\colon \mathbb {R} ^{n}\rightarrow \mathbb {R} } X ⊂ R n {\displaystyle X\subset \mathbb {R} ^{n}} ⋃ x 0 ∈ X ∂ f ( x 0 ) {\displaystyle \bigcup _{x_{0}\in X}\partial f(x_{0})}
Sei f : R n → R {\displaystyle f\colon \mathbb {R} ^{n}\rightarrow \mathbb {R} } X ⊂ R n {\displaystyle X\subset \mathbb {R} ^{n}} ε := sup | f ( U 1 ( X ) ¯ ) | {\displaystyle \varepsilon :=\sup |f({\overline {U_{1}(X)}})|} U 1 ( X ) ¯ = { x ∈ R n ∣ d i s t ( x , X ) ≤ 1 } {\displaystyle {\overline {U_{1}(X)}}=\{x\in \mathbb {R} ^{n}\mid {\rm {dist}}(x,X)\leq 1\}} ⋃ x 0 ∈ X ∂ f ( x 0 ) {\displaystyle \bigcup _{x_{0}\in X}\partial f(x_{0})} R := 2 ε {\displaystyle R:=2\varepsilon } x 0 ∈ X {\displaystyle x_{0}\in X} g ∈ ∂ f ( x 0 ) {\displaystyle g\in \partial f(x_{0})} ‖ g ‖ 2 > R = 2 ε {\displaystyle \|g\|_{2}>R=2\varepsilon } x := 1 ‖ g ‖ 2 g + x 0 {\displaystyle x:={\frac {1}{\|g\|_{2}}}g+x_{0}} x 0 , x ∈ U 1 ( X ) ¯ {\displaystyle x_{0},x\in {\overline {U_{1}(X)}}}
g T ( x − x 0 ) = 1 ‖ g ‖ 2 g T g = ‖ g ‖ 2 > 2 ε ≥ | f ( x ) − f ( x 0 ) | ≥ f ( x ) − f ( x 0 ) {\displaystyle g^{T}(x-x_{0})={\frac {1}{\|g\|_{2}}}g^{T}g=\|g\|_{2}>2\varepsilon \geq \left|f(x)-f(x_{0})\right|\geq f(x)-f(x_{0})} g {\displaystyle g}
Ist die Funktion differenzierbar in x 0 ∈ i n t d o m f {\displaystyle x_{0}\in \mathrm {int} \,\mathrm {dom} \,f}
∂ f ( x 0 ) = { ∇ f ( x 0 ) } {\displaystyle \partial f(x_{0})=\left\{\nabla f(x_{0})\right\}} Siehe [ 3]
Zudem gilt: Ist das Subdifferential ∂ f ( x 0 ) {\displaystyle \partial f(x_{0})} f {\displaystyle f} x 0 {\displaystyle x_{0}} [ 4]
↑ R. T. Rockafellar Convex analysis 1970., p.214↑ R. T. Rockafellar Convex analysis 1970., p.215↑ Yaron Singer: Advanced Optimzation. Abgerufen am 27. Januar 2022 : „Proposition 4“ ↑ R. T. Rockafellar: Convex Analysis . Band 28 , 1970: „Theorem 25.1“ 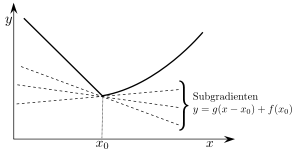


 French
French Deutsch
Deutsch









![{\displaystyle [a,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9c4b788fc5c637e26ee98b45f89a5c08c85f7935)
![{\displaystyle \partial f(x_{0}):=[a,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/eef8efa37ce03d6bfec0b3806cf42ed102c5ee31)













![{\displaystyle \partial f(x_{0})={\begin{cases}\{-1\}&x_{0}<0\\\left[-1,1\right]&x_{0}=0\\\{1\}&x_{0}>0\end{cases}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a99132d53aa509f119f4213b458e1ec44ebce038)













