In der Trigonometrie stellt der Tangenssatz (auch Tangentensatz und Regel von Napier ) eine Beziehung zwischen den drei Seiten eines ebenen Dreiecks und dem Tangens der halben Summe bzw. der halben Differenz zweier Winkel des Dreiecks her.
Für die drei Seiten a , b und c eines Dreiecks sowie für die diesen Seiten jeweils gegenüber liegenden Winkel α, β und γ gilt:
b + c b − c = tan β + γ 2 tan β − γ 2 {\displaystyle {\frac {b+c}{b-c}}={\frac {\tan {\frac {\beta +\gamma }{2}}}{\tan {\frac {\beta -\gamma }{2}}}}} Wegen
tan β + γ 2 = tan 180 ∘ − α 2 = tan ( 90 ∘ − α 2 ) = cot α 2 {\displaystyle \tan {\frac {\beta +\gamma }{2}}=\tan {\frac {180^{\circ }-\alpha }{2}}=\tan \left(90^{\circ }-{\frac {\alpha }{2}}\right)=\cot {\frac {\alpha }{2}}} kann man diese Formel auch schreiben als
b + c b − c = cot α 2 tan β − γ 2 {\displaystyle {\frac {b+c}{b-c}}={\frac {\cot {\frac {\alpha }{2}}}{\tan {\frac {\beta -\gamma }{2}}}}} Analoge Formeln für a + b a − b {\displaystyle {\frac {a+b}{a-b}}} a + c a − c {\displaystyle {\frac {a+c}{a-c}}} zyklische Vertauschung :
a + b a − b = tan α + β 2 tan α − β 2 = cot γ 2 tan α − β 2 {\displaystyle {\frac {a+b}{a-b}}={\frac {\tan {\frac {\alpha +\beta }{2}}}{\tan {\frac {\alpha -\beta }{2}}}}={\frac {\cot {\frac {\gamma }{2}}}{\tan {\frac {\alpha -\beta }{2}}}}} c + a c − a = tan γ + α 2 tan γ − α 2 = cot β 2 tan γ − α 2 {\displaystyle {\frac {c+a}{c-a}}={\frac {\tan {\frac {\gamma +\alpha }{2}}}{\tan {\frac {\gamma -\alpha }{2}}}}={\frac {\cot {\frac {\beta }{2}}}{\tan {\frac {\gamma -\alpha }{2}}}}} Wegen tan ( − x ) = − tan ( x ) {\displaystyle \tan(-x)=-\tan(x)}
a + c a − c = tan α + γ 2 tan α − γ 2 = cot β 2 tan α − γ 2 {\displaystyle {\frac {a+c}{a-c}}={\frac {\tan {\frac {\alpha +\gamma }{2}}}{\tan {\frac {\alpha -\gamma }{2}}}}={\frac {\cot {\frac {\beta }{2}}}{\tan {\frac {\alpha -\gamma }{2}}}}} Nach dem Sinussatz gilt b c = sin β sin γ {\displaystyle {\tfrac {b}{c}}={\tfrac {\sin \beta }{\sin \gamma }}}
b + c b − c = b c + 1 b c − 1 = sin β sin γ + sin γ sin γ sin β sin γ − sin γ sin γ = sin β + sin γ sin β − sin γ , {\displaystyle {\frac {b+c}{b-c}}={\frac {{\frac {b}{c}}+1}{{\frac {b}{c}}-1}}={\frac {{\frac {\sin \beta }{\sin \gamma }}+{\frac {\sin \gamma }{\sin \gamma }}}{{\frac {\sin \beta }{\sin \gamma }}-{\frac {\sin \gamma }{\sin \gamma }}}}={\frac {\sin \beta +\sin \gamma }{\sin \beta -\sin \gamma }},} nach Einsetzen der Identitäten
sin β + sin γ = 2 sin β + γ 2 cos β − γ 2 . {\displaystyle \sin \beta +\sin \gamma =2\sin {\frac {\beta +\gamma }{2}}\cos {\frac {\beta -\gamma }{2}}.} sowie
sin β − sin γ = 2 cos β + γ 2 sin β − γ 2 {\displaystyle \sin \beta -\sin \gamma =2\cos {\frac {\beta +\gamma }{2}}\sin {\frac {\beta -\gamma }{2}}} die sich aus den Additionstheoremen ableiten lassen, ergibt sich per Division die gewünschte Formel.
Mit Winkelsumme im Dreieck und Übergang zum Komplementärwinkel :
tan β + γ 2 = tan 180 ∘ − α 2 = tan ( 90 ∘ − α 2 ) = cot α 2 {\displaystyle \tan {\frac {\beta +\gamma }{2}}=\tan {\frac {180^{\circ }-\alpha }{2}}=\tan \left(90^{\circ }-{\frac {\alpha }{2}}\right)=\cot {\frac {\alpha }{2}}\qquad } Aus den Mollweideschen Formeln folgt mit (1):
b + c b − c = b + c a ⋅ a b − c = cos β − γ 2 sin α 2 ⋅ cos α 2 sin β − γ 2 = cot β − γ 2 ⋅ cot α 2 = cot α 2 tan β − γ 2 = tan β + γ 2 tan β − γ 2 {\displaystyle {\frac {b+c}{b-c}}={\frac {b+c}{a}}\cdot {\frac {a}{b-c}}={\frac {\cos {\frac {\beta -\gamma }{2}}}{\sin {\frac {\alpha }{2}}}}\cdot {\frac {\cos {\frac {\alpha }{2}}}{\sin {\frac {\beta -\gamma }{2}}}}=\cot {\frac {\beta -\gamma }{2}}\cdot \cot {\frac {\alpha }{2}}={\frac {\cot {\frac {\alpha }{2}}}{\tan {\frac {\beta -\gamma }{2}}}}={\frac {\tan {\frac {\beta +\gamma }{2}}}{\tan {\frac {\beta -\gamma }{2}}}}\quad } 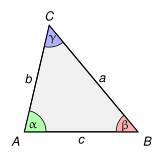


 French
French Deutsch
Deutsch













