Function of several complex variables

The theory of functions of several complex variables is the branch of mathematics dealing with functions defined on the complex coordinate space ${\displaystyle \mathbb {C} ^{n}}$, that is, n-tuples of complex numbers. The name of the field dealing with the properties of these functions is called several complex variables (and analytic space), which the Mathematics Subject Classification has as a top-level heading.

As in complex analysis of functions of one variable, which is the case n = 1, the functions studied are holomorphic or complex analytic so that, locally, they are power series in the variables z_i. Equivalently, they are locally uniform limits of polynomials; or locally square-integrable solutions to the n-dimensional Cauchy–Riemann equations.^[1][2][3] For one complex variable, every domain^{[note 1]}(${\displaystyle D\subset \mathbb {C} }$), is the domain of holomorphy of some function, in other words every domain has a function for which it is the domain of holomorphy.^[4][5] For several complex variables, this is not the case; there exist domains (${\displaystyle D\subset \mathbb {C} ^{n},\ n\geq 2}$) that are not the domain of holomorphy of any function, and so is not always the domain of holomorphy, so the domain of holomorphy is one of the themes in this field.^[4] Patching the local data of meromorphic functions, i.e. the problem of creating a global meromorphic function from zeros and poles, is called the Cousin problem. Also, the interesting phenomena that occur in several complex variables are fundamentally important to the study of compact complex manifolds and complex projective varieties (${\displaystyle \mathbb {CP} ^{n}}$)^[6] and has a different flavour to complex analytic geometry in ${\displaystyle \mathbb {C} ^{n}}$ or on Stein manifolds, these are much similar to study of algebraic varieties that is study of the algebraic geometry than complex analytic geometry.

Many examples of such functions were familiar in nineteenth-century mathematics; abelian functions, theta functions, and some hypergeometric series, and also, as an example of an inverse problem; the Jacobi inversion problem.^[7] Naturally also same function of one variable that depends on some complex parameter is a candidate. The theory, however, for many years didn't become a full-fledged field in mathematical analysis, since its characteristic phenomena weren't uncovered. The Weierstrass preparation theorem would now be classed as commutative algebra; it did justify the local picture, ramification, that addresses the generalization of the branch points of Riemann surface theory.

With work of Friedrich Hartogs, Pierre Cousin [fr], E. E. Levi, and of Kiyoshi Oka in the 1930s, a general theory began to emerge; others working in the area at the time were Heinrich Behnke, Peter Thullen, Karl Stein, Wilhelm Wirtinger and Francesco Severi. Hartogs proved some basic results, such as every isolated singularity is removable, for every analytic function $${\displaystyle f:\mathbb {C} ^{n}\to \mathbb {C} }$$ whenever n > 1. Naturally the analogues of contour integrals will be harder to handle; when n = 2 an integral surrounding a point should be over a three-dimensional manifold (since we are in four real dimensions), while iterating contour (line) integrals over two separate complex variables should come to a double integral over a two-dimensional surface. This means that the residue calculus will have to take a very different character.

After 1945 important work in France, in the seminar of Henri Cartan, and Germany with Hans Grauert and Reinhold Remmert, quickly changed the picture of the theory. A number of issues were clarified, in particular that of analytic continuation. Here a major difference is evident from the one-variable theory; while for every open connected set D in ${\displaystyle \mathbb {C} }$ we can find a function that will nowhere continue analytically over the boundary, that cannot be said for n > 1. In fact the D of that kind are rather special in nature (especially in complex coordinate spaces ${\displaystyle \mathbb {C} ^{n}}$ and Stein manifolds, satisfying a condition called pseudoconvexity). The natural domains of definition of functions, continued to the limit, are called Stein manifolds and their nature was to make sheaf cohomology groups vanish, on the other hand, the Grauert–Riemenschneider vanishing theorem is known as a similar result for compact complex manifolds, and the Grauert–Riemenschneider conjecture is a special case of the conjecture of Narasimhan.^[4] In fact it was the need to put (in particular) the work of Oka on a clearer basis that led quickly to the consistent use of sheaves for the formulation of the theory (with major repercussions for algebraic geometry, in particular from Grauert's work).

From this point onwards there was a foundational theory, which could be applied to analytic geometry, ^{[note 2]} automorphic forms of several variables, and partial differential equations. The deformation theory of complex structures and complex manifolds was described in general terms by Kunihiko Kodaira and D. C. Spencer. The celebrated paper GAGA of Serre^[8] pinned down the crossover point from géometrie analytique to géometrie algébrique.

C. L. Siegel was heard to complain that the new theory of functions of several complex variables had few functions in it, meaning that the special function side of the theory was subordinated to sheaves. The interest for number theory, certainly, is in specific generalizations of modular forms. The classical candidates are the Hilbert modular forms and Siegel modular forms. These days these are associated to algebraic groups (respectively the Weil restriction from a totally real number field of GL(2), and the symplectic group), for which it happens that automorphic representations can be derived from analytic functions. In a sense this doesn't contradict Siegel; the modern theory has its own, different directions.

Subsequent developments included the hyperfunction theory, and the edge-of-the-wedge theorem, both of which had some inspiration from quantum field theory. There are a number of other fields, such as Banach algebra theory, that draw on several complex variables.

The complex coordinate space ${\displaystyle \mathbb {C} ^{n}}$ is the Cartesian product of n copies of ${\displaystyle \mathbb {C} }$, and when ${\displaystyle \mathbb {C} ^{n}}$ is a domain of holomorphy, ${\displaystyle \mathbb {C} ^{n}}$ can be regarded as a Stein manifold, and more generalized Stein space. ${\displaystyle \mathbb {C} ^{n}}$ is also considered to be a complex projective variety, a Kähler manifold,^[9] etc. It is also an n-dimensional vector space over the complex numbers, which gives its dimension 2n over ${\displaystyle \mathbb {R} }$.^{[note 3]} Hence, as a set and as a topological space, ${\displaystyle \mathbb {C} ^{n}}$ may be identified to the real coordinate space ${\displaystyle \mathbb {R} ^{2n}}$ and its topological dimension is thus 2n.

In coordinate-free language, any vector space over complex numbers may be thought of as a real vector space of twice as many dimensions, where a complex structure is specified by a linear operator J (such that J ² = −I) which defines multiplication by the imaginary unit i.

Any such space, as a real space, is oriented. On the complex plane thought of as a Cartesian plane, multiplication by a complex number w = u + iv may be represented by the real matrix

${\displaystyle {\begin{pmatrix}u&-v\\v&u\end{pmatrix}},}$

with determinant

${\displaystyle u^{2}+v^{2}=|w|^{2}.}$

Likewise, if one expresses any finite-dimensional complex linear operator as a real matrix (which will be composed from 2 × 2 blocks of the aforementioned form), then its determinant equals to the square of absolute value of the corresponding complex determinant. It is a non-negative number, which implies that the (real) orientation of the space is never reversed by a complex operator. The same applies to Jacobians of holomorphic functions from ${\displaystyle \mathbb {C} ^{n}}$ to ${\displaystyle \mathbb {C} ^{n}}$.

A function f defined on a domain ${\displaystyle D\subset \mathbb {C} ^{n}}$ and with values in ${\displaystyle \mathbb {C} }$ is said to be holomorphic at a point ${\displaystyle z\in D}$ if it is complex-differentiable at this point, in the sense that there exists a complex linear map ${\displaystyle L:\mathbb {C} ^{n}\to \mathbb {C} }$ such that

${\displaystyle f(z+h)=f(z)+L(h)+o(\lVert h\rVert )}$

The function f is said to be holomorphic if it is holomorphic at all points of its domain of definition D.

If f is holomorphic, then all the partial maps :

${\displaystyle z\mapsto f(z_{1},\dots ,z_{i-1},z,z_{i+1},\dots ,z_{n})}$

are holomorphic as functions of one complex variable : we say that f is holomorphic in each variable separately. Conversely, if f is holomorphic in each variable separately, then f is in fact holomorphic : this is known as Hartog's theorem, or as Osgood's lemma under the additional hypothesis that f is continuous.

In one complex variable, a function ${\displaystyle f:\mathbb {C} \to \mathbb {C} }$ defined on the plane is holomorphic at a point ${\displaystyle p\in \mathbb {C} }$ if and only if its real part ${\displaystyle u}$ and its imaginary part ${\displaystyle v}$ satisfy the so-called Cauchy-Riemann equations at ${\displaystyle p}$ : $${\displaystyle {\frac {\partial u}{\partial x}}(p)={\frac {\partial v}{\partial y}}(p)\quad {\text{ and }}\quad {\frac {\partial u}{\partial y}}(p)=-{\frac {\partial v}{\partial x}}(p)}$$

In several variables, a function ${\displaystyle f:\mathbb {C} ^{n}\to \mathbb {C} }$ is holomorphic if and only if it is holomorphic in each variable separately, and hence if and only if the real part ${\displaystyle u}$ and the imaginary part ${\displaystyle v}$ of ${\displaystyle f}$ satisfiy the Cauchy Riemann equations : $${\displaystyle \forall i\in \{1,\dots ,n\},\quad {\frac {\partial u}{\partial x_{i}}}={\frac {\partial v}{\partial y_{i}}}\quad {\text{ and }}\quad {\frac {\partial u}{\partial y_{i}}}=-{\frac {\partial v}{\partial x_{i}}}}$$

Using the formalism of Wirtinger derivatives, this can be reformulated as : $${\displaystyle \forall i\in \{1,\dots ,n\},\quad {\frac {\partial f}{\partial {\overline {z_{i}}}}}=0,}$$ or even more compactly using the formalism of complex differential forms, as : $${\displaystyle {\bar {\partial }}f=0.}$$

Prove the sufficiency of two conditions (A) and (B). Let f meets the conditions of being continuous and separately homorphic on domain D. Each disk has a rectifiable curve ${\displaystyle \gamma }$, ${\displaystyle \gamma _{\nu }}$ is piecewise smoothness, class ${\displaystyle {\mathcal {C}}^{1}}$ Jordan closed curve. (${\displaystyle \nu =1,2,\ldots ,n}$) Let ${\displaystyle D_{\nu }}$ be the domain surrounded by each ${\displaystyle \gamma _{\nu }}$. Cartesian product closure ${\displaystyle {\overline {D_{1}\times D_{2}\times \cdots \times D_{n}}}}$ is ${\displaystyle {\overline {D_{1}\times D_{2}\times \cdots \times D_{n}}}\in D}$. Also, take the closed polydisc ${\displaystyle {\overline {\Delta }}}$ so that it becomes ${\displaystyle {\overline {\Delta }}\subset {D_{1}\times D_{2}\times \cdots \times D_{n}}}$. (${\displaystyle {\overline {\Delta }}(z,r)=\left\{\zeta =(\zeta _{1},\zeta _{2},\dots ,\zeta _{n})\in \mathbb {C} ^{n};\left|\zeta _{\nu }-z_{\nu }\right|\leq r_{\nu }{\text{ for all }}\nu =1,\dots ,n\right\}}$ and let ${\displaystyle \{z\}_{\nu =1}^{n}}$ be the center of each disk.) Using the Cauchy's integral formula of one variable repeatedly, ^{[note 4]}

${\displaystyle {\begin{aligned}f(z_{1},\ldots ,z_{n})&={\frac {1}{2\pi i}}\int _{\partial D_{1}}{\frac {f(\zeta _{1},z_{2},\ldots ,z_{n})}{\zeta _{1}-z_{1}}}\,d\zeta _{1}\\[6pt]&={\frac {1}{(2\pi i)^{2}}}\int _{\partial D_{2}}\,d\zeta _{2}\int _{\partial D_{1}}{\frac {f(\zeta _{1},\zeta _{2},z_{3},\ldots ,z_{n})}{(\zeta _{1}-z_{1})(\zeta _{2}-z_{2})}}\,d\zeta _{1}\\[6pt]&={\frac {1}{(2\pi i)^{n}}}\int _{\partial D_{n}}\,d\zeta _{n}\cdots \int _{\partial D_{2}}\,d\zeta _{2}\int _{\partial D_{1}}{\frac {f(\zeta _{1},\zeta _{2},\ldots ,\zeta _{n})}{(\zeta _{1}-z_{1})(\zeta _{2}-z_{2})\cdots (\zeta _{n}-z_{n})}}\,d\zeta _{1}\end{aligned}}}$

Because ${\displaystyle \partial D}$ is a rectifiable Jordanian closed curve^{[note 5]} and f is continuous, so the order of products and sums can be exchanged so the iterated integral can be calculated as a multiple integral. Therefore,

${\displaystyle f(z_{1},\dots ,z_{n})={\frac {1}{(2\pi i)^{n}}}\int _{\partial D_{1}}\cdots \int _{\partial D_{n}}{\frac {f(\zeta _{1},\dots ,\zeta _{n})}{(\zeta _{1}-z_{1})\cdots (\zeta _{n}-z_{n})}}\,d\zeta _{1}\cdots d\zeta _{n}}$

(1)

Because the order of products and sums is interchangeable, from (1) we get

${\displaystyle {\frac {\partial ^{k_{1}+\cdots +k_{n}}f(\zeta _{1},\zeta _{2},\ldots ,\zeta _{n})}{\partial {z_{1}}^{k_{1}}\cdots \partial {z_{n}}^{k_{n}}}}={\frac {k_{1}\cdots k_{n}!}{(2\pi i)^{n}}}\int _{\partial D_{1}}\cdots \int _{\partial D_{n}}{\frac {f(\zeta _{1},\dots ,\zeta _{n})}{(\zeta _{1}-z_{1})^{k_{1}+1}\cdots (\zeta _{n}-z_{n})^{k_{n}+1}}}\,d\zeta _{1}\cdots d\zeta _{n}.}$

(2)

f is class ${\displaystyle {\mathcal {C}}^{\infty }}$-function.

From (2), if f is holomorphic, on polydisc ${\displaystyle \left\{\zeta =(\zeta _{1},\zeta _{2},\dots ,\zeta _{n})\in \mathbb {C} ^{n};|\zeta _{\nu }-z_{\nu }|\leq r_{\nu },{\text{ for all }}\nu =1,\dots ,n\right\}}$ and ${\displaystyle |f|\leq {M}}$, the following evaluation equation is obtained.

${\displaystyle \left|{\frac {\partial ^{k_{1}+\cdots +k_{n}}f(\zeta _{1},\zeta _{2},\ldots ,\zeta _{n})}{{\partial z_{1}}^{k_{1}}\cdots \partial {z_{n}}^{k_{n}}}}\right|\leq {\frac {Mk_{1}\cdots k_{n}!}{{r_{1}}^{k_{1}}\cdots {r_{n}}^{k_{n}}}}}$

Therefore, Liouville's theorem hold.

If function f is holomorphic, on polydisc ${\displaystyle \{z=(z_{1},z_{2},\dots ,z_{n})\in \mathbb {C} ^{n};|z_{\nu }-a_{\nu }|<r_{\nu },{\text{ for all }}\nu =1,\dots ,n\}}$, from the Cauchy's integral formula, we can see that it can be uniquely expanded to the next power series.

${\displaystyle {\begin{aligned}&f(z)=\sum _{k_{1},\dots ,k_{n}=0}^{\infty }c_{k_{1},\dots ,k_{n}}(z_{1}-a_{1})^{k_{1}}\cdots (z_{n}-a_{n})^{k_{n}}\ ,\\&c_{k_{1}\cdots k_{n}}={\frac {1}{(2\pi i)^{n}}}\int _{\partial D_{1}}\cdots \int _{\partial D_{n}}{\frac {f(\zeta _{1},\dots ,\zeta _{n})}{(\zeta _{1}-a_{1})^{k_{1}+1}\cdots (\zeta _{n}-a_{n})^{k_{n}+1}}}\,d\zeta _{1}\cdots d\zeta _{n}\end{aligned}}}$

In addition, f that satisfies the following conditions is called an analytic function.

For each point ${\displaystyle a=(a_{1},\dots ,a_{n})\in D\subset \mathbb {C} ^{n}}$, ${\displaystyle f(z)}$ is expressed as a power series expansion that is convergent on D :

${\displaystyle f(z)=\sum _{k_{1},\dots ,k_{n}=0}^{\infty }c_{k_{1},\dots ,k_{n}}(z_{1}-a_{1})^{k_{1}}\cdots (z_{n}-a_{n})^{k_{n}}\ ,}$

We have already explained that holomorphic functions on polydisc are analytic. Also, from the theorem derived by Weierstrass, we can see that the analytic function on polydisc (convergent power series) is holomorphic.

If a sequence of functions ${\displaystyle f_{1},\ldots ,f_{n}}$ which converges uniformly on compacta inside a domain D, the limit function f of ${\displaystyle f_{v}}$ also uniformly on compacta inside a domain D. Also, respective partial derivative of ${\displaystyle f_{v}}$ also compactly converges on domain D to the corresponding derivative of f.

${\displaystyle {\frac {\partial ^{k_{1}+\cdots +k_{n}}f}{\partial {z_{1}}^{k_{1}}\cdots \partial {z_{n}}^{k_{n}}}}=\sum _{v=1}^{\infty }{\frac {\partial ^{k_{1}+\cdots +k_{n}}f_{v}}{\partial {z_{1}}^{k_{1}}\cdots \partial {z_{n}}^{k_{n}}}}}$^[10]

It is possible to define a combination of positive real numbers ${\displaystyle \{r_{\nu }\ (\nu =1,\dots ,n)\}}$ such that the power series ${\textstyle \sum _{k_{1},\dots ,k_{n}=0}^{\infty }c_{k_{1},\dots ,k_{n}}(z_{1}-a_{1})^{k_{1}}\cdots (z_{n}-a_{n})^{k_{n}}\ }$ converges uniformly at ${\displaystyle \left\{z=(z_{1},z_{2},\dots ,z_{n})\in \mathbb {C} ^{n};|z_{\nu }-a_{\nu }|<r_{\nu },{\text{ for all }}\nu =1,\dots ,n\right\}}$ and does not converge uniformly at ${\displaystyle \left\{z=(z_{1},z_{2},\dots ,z_{n})\in \mathbb {C} ^{n};|z_{\nu }-a_{\nu }|>r_{\nu },{\text{ for all }}\nu =1,\dots ,n\right\}}$.

In this way it is possible to have a similar, combination of radius of convergence^{[note 6]} for a one complex variable. This combination is generally not unique and there are an infinite number of combinations.

Let ${\displaystyle \omega (z)}$ be holomorphic in the annulus ${\displaystyle \left\{z=(z_{1},z_{2},\dots ,z_{n})\in \mathbb {C} ^{n};r_{\nu }<|z|<R_{\nu },{\text{ for all }}\nu +1,\dots ,n\right\}}$ and continuous on their circumference, then there exists the following expansion ;

${\displaystyle {\begin{aligned}\omega (z)&=\sum _{k=0}^{\infty }{\frac {1}{k!}}{\frac {1}{(2\pi i)^{n}}}\int _{|\zeta _{\nu }|=R_{\nu }}\cdots \int \omega (\zeta )\times \left[{\frac {d^{k}}{dz^{k}}}{\frac {1}{\zeta -z}}\right]_{z=0}df_{\zeta }\cdot z^{k}\\[6pt]&+\sum _{k=1}^{\infty }{\frac {1}{k!}}{\frac {1}{2\pi i}}\int _{|\zeta _{\nu }|=r_{\nu }}\cdots \int \omega (\zeta )\times \left(0,\cdots ,{\sqrt {\frac {k!}{\alpha _{1}!\cdots \alpha _{n}!}}}\cdot \zeta _{n}^{\alpha _{1}-1}\cdots \zeta _{n}^{\alpha _{n}-1},\cdots 0\right)df_{\zeta }\cdot {\frac {1}{z^{k}}}\ (\alpha _{1}+\cdots +\alpha _{n}=k)\end{aligned}}}$

The integral in the second term, of the right-hand side is performed so as to see the zero on the left in every plane, also this integrated series is uniformly convergent in the annulus ${\displaystyle r'_{\nu }<|z|<R'_{\nu }}$, where ${\displaystyle r'_{\nu }>r_{\nu }}$ and ${\displaystyle R'_{\nu }<R_{\nu }}$, and so it is possible to integrate term.^[11]

The Cauchy integral formula holds only for polydiscs, and in the domain of several complex variables, polydiscs are only one of many possible domains, so we introduce the Bochner–Martinelli formula.

Suppose that f is a continuously differentiable function on the closure of a domain D on ${\displaystyle \mathbb {C} ^{n}}$ with piecewise smooth boundary ${\displaystyle \partial D}$, and let the symbol ${\displaystyle \land }$ denotes the exterior or wedge product of differential forms. Then the Bochner–Martinelli formula states that if z is in the domain D then, for ${\displaystyle \zeta }$, z in ${\displaystyle \mathbb {C} ^{n}}$ the Bochner–Martinelli kernel ${\displaystyle \omega (\zeta ,z)}$ is a differential form in ${\displaystyle \zeta }$ of bidegree ${\displaystyle (n,n-1)}$, defined by

${\displaystyle \omega (\zeta ,z)={\frac {(n-1)!}{(2\pi i)^{n}}}{\frac {1}{|z-\zeta |^{2n}}}\sum _{1\leq j\leq n}({\overline {\zeta }}_{j}-{\overline {z}}_{j})\,d{\overline {\zeta }}_{1}\land d\zeta _{1}\land \cdots \land d\zeta _{j}\land \cdots \land d{\overline {\zeta }}_{n}\land d\zeta _{n}}$

${\displaystyle \displaystyle f(z)=\int _{\partial D}f(\zeta )\omega (\zeta ,z)-\int _{D}{\overline {\partial }}f(\zeta )\land \omega (\zeta ,z).}$

In particular if f is holomorphic the second term vanishes, so

${\displaystyle \displaystyle f(z)=\int _{\partial D}f(\zeta )\omega (\zeta ,z).}$

Holomorphic functions of several complex variables satisfy an identity theorem, as in one variable : two holomorphic functions defined on the same connected open set ${\displaystyle D\subset \mathbb {C} ^{n}}$ and which coincide on an open subset N of D, are equal on the whole open set D. This result can be proven from the fact that holomorphics functions have power series extensions, and it can also be deduced from the one variable case. Contrary to the one variable case, it is possible that two different holomorphic functions coincide on a set which has an accumulation point, for instance the maps ${\displaystyle f(z_{1},z_{2})=0}$ and ${\displaystyle g(z_{1},z_{2})=z_{1}}$coincide on the whole complex line of ${\displaystyle \mathbb {C} ^{2}}$ defined by the equation ${\displaystyle z_{1}=0}$.

The maximal principle, inverse function theorem, and implicit function theorems also hold. For a generalized version of the implicit function theorem to complex variables, see the Weierstrass preparation theorem.

From the establishment of the inverse function theorem, the following mapping can be defined.

For the domain U, V of the n-dimensional complex space ${\displaystyle \mathbb {C} ^{n}}$, the bijective holomorphic function ${\displaystyle \phi :U\to V}$ and the inverse mapping ${\displaystyle \phi ^{-1}:V\to U}$ is also holomorphic. At this time, ${\displaystyle \phi }$ is called a U, V biholomorphism also, we say that U and V are biholomorphically equivalent or that they are biholomorphic.

When ${\displaystyle n>1}$, open balls and open polydiscs are not biholomorphically equivalent, that is, there is no biholomorphic mapping between the two.^[12] This was proven by Poincaré in 1907 by showing that their automorphism groups have different dimensions as Lie groups.^[5][13] However, even in the case of several complex variables, there are some results similar to the results of the theory of uniformization in one complex variable.^[14]

Let U, V be domain on ${\displaystyle \mathbb {C} ^{n}}$, such that ${\displaystyle f\in {\mathcal {O}}(U)}$ and ${\displaystyle g\in {\mathcal {O}}(V)}$, (${\displaystyle {\mathcal {O}}(U)}$ is the set/ring of holomorphic functions on U.) assume that ${\displaystyle U,\ V,\ U\cap V\neq \varnothing }$ and ${\displaystyle W}$ is a connected component of ${\displaystyle U\cap V}$. If ${\displaystyle f|_{W}=g|_{W}}$ then f is said to be connected to V, and g is said to be analytic continuation of f. From the identity theorem, if g exists, for each way of choosing W it is unique. When n > 2, the following phenomenon occurs depending on the shape of the boundary ${\displaystyle \partial U}$: there exists domain U, V, such that all holomorphic functions ${\displaystyle f}$ over the domain U, have an analytic continuation ${\displaystyle g\in {\mathcal {O}}(V)}$. In other words, there may be not exist a function ${\displaystyle f\in {\mathcal {O}}(U)}$ such that ${\displaystyle \partial U}$ as the natural boundary. There is called the Hartogs's phenomenon. Therefore, researching when domain boundaries become natural boundaries has become one of the main research themes of several complex variables. In addition, when ${\displaystyle n\geq 2}$, it would be that the above V has an intersection part with U other than W. This contributed to advancement of the notion of sheaf cohomology.

In polydisks, the Cauchy's integral formula holds and the power series expansion of holomorphic functions is defined, but polydisks and open unit balls are not biholomorphic mapping because the Riemann mapping theorem does not hold, and also, polydisks was possible to separation of variables, but it doesn't always hold for any domain. Therefore, in order to study of the domain of convergence of the power series, it was necessary to make additional restriction on the domain, this was the Reinhardt domain. Early knowledge into the properties of field of study of several complex variables, such as Logarithmically-convex, Hartogs's extension theorem, etc., were given in the Reinhardt domain.

Let ${\displaystyle D\subset \mathbb {C} ^{n}}$ (${\displaystyle n\geq 1}$) to be a domain, with centre at a point ${\displaystyle a=(a_{1},\dots ,a_{n})\in \mathbb {C} ^{n}}$, such that, together with each point ${\displaystyle z^{0}=(z_{1}^{0},\dots ,z_{n}^{0})\in D}$, the domain also contains the set

${\displaystyle \left\{z=(z_{1},\dots ,z_{n});\left|z_{\nu }-a_{\nu }\right|=\left|z_{\nu }^{0}-a_{\nu }\right|,\ \nu =1,\dots ,n\right\}.}$

A domain D is called a Reinhardt domain if it satisfies the following conditions:^[15][16]

Let ${\displaystyle \theta _{\nu }\;(\nu =1,\dots ,n)}$ is a arbitrary real numbers, a domain D is invariant under the rotation: ${\displaystyle \left\{z^{0}-a_{\nu }\right\}\to \left\{e^{i\theta _{\nu }}(z_{\nu }^{0}-a_{\nu })\right\}}$.

The Reinhardt domains which are defined by the following condition; Together with all points of ${\displaystyle z^{0}\in D}$, the domain contains the set

${\displaystyle \left\{z=(z_{1},\dots ,z_{n});z=a+\left(z^{0}-a\right)e^{i\theta },\ 0\leq \theta <2\pi \right\}.}$

A Reinhardt domain D is called a complete Reinhardt domain with centre at a point a if together with all point ${\displaystyle z^{0}\in D}$ it also contains the polydisc

${\displaystyle \left\{z=(z_{1},\dots ,z_{n});\left|z_{\nu }-a_{\nu }\right|\leq \left|z_{\nu }^{0}-a_{\nu }\right|,\ \nu =1,\dots ,n\right\}.}$

A complete Reinhardt domain D is star-like with regard to its centre a. Therefore, the complete Reinhardt domain is simply connected, also when the complete Reinhardt domain is the boundary line, there is a way to prove the Cauchy's integral theorem without using the Jordan curve theorem.

When a some complete Reinhardt domain to be the domain of convergence of a power series, an additional condition is required, which is called logarithmically-convex.

A Reinhardt domain D is called logarithmically convex if the image ${\displaystyle \lambda (D^{*})}$ of the set

${\displaystyle D^{*}=\{z=(z_{1},\dots ,z_{n})\in D;z_{1},\dots ,z_{n}\neq 0\}}$

under the mapping

${\displaystyle \lambda ;z\rightarrow \lambda (z)=(\ln |z_{1}|,\dots ,\ln |z_{n}|)}$

is a convex set in the real coordinate space ${\displaystyle \mathbb {R} ^{n}}$.

Every such domain in ${\displaystyle \mathbb {C} ^{n}}$ is the interior of the set of points of absolute convergence of some power series in ${\textstyle \sum _{k_{1},\dots ,k_{n}=0}^{\infty }c_{k_{1},\dots ,k_{n}}(z_{1}-a_{1})^{k_{1}}\cdots (z_{n}-a_{n})^{k_{n}}\ }$, and conversely; The domain of convergence of every power series in ${\displaystyle z_{1},\dots ,z_{n}}$ is a logarithmically-convex Reinhardt domain with centre ${\displaystyle a=0}$. ^{[note 7]} But, there is an example of a complete Reinhardt domain D which is not logarithmically convex.^[17]

When examining the domain of convergence on the Reinhardt domain, Hartogs found the Hartogs's phenomenon in which holomorphic functions in some domain on the ${\displaystyle \mathbb {C} ^{n}}$ were all connected to larger domain.^[18]

On the polydisk consisting of two disks ${\displaystyle \Delta ^{2}=\{z\in \mathbb {C} ^{2};|z_{1}|<1,|z_{2}|<1\}}$ when ${\displaystyle 0<\varepsilon <1}$.

Internal domain of ${\displaystyle H_{\varepsilon }=\{z=(z_{1},z_{2})\in \Delta ^{2};|z_{1}|<\varepsilon \ \cup \ 1-\varepsilon <|z_{2}|\}\ (0<\varepsilon <1)}$

Hartogs's extension theorem (1906);^[19] Let f be a holomorphic function on a set G \ K, where G is a bounded (surrounded by a rectifiable closed Jordan curve) domain^{[note 8]} on ${\displaystyle \mathbb {C} ^{n}}$ (n ≥ 2) and K is a compact subset of G. If the complement G \ K is connected, then every holomorphic function f regardless of how it is chosen can be each extended to a unique holomorphic function on G.^[21][20]

It is also called Osgood–Brown theorem is that for holomorphic functions of several complex variables, the singularity is a accumulation point, not an isolated point. This means that the various properties that hold for holomorphic functions of one-variable complex variables do not hold for holomorphic functions of several complex variables. The nature of these singularities is also derived from Weierstrass preparation theorem. A generalization of this theorem using the same method as Hartogs was proved in 2007.^[22][23]

From Hartogs's extension theorem the domain of convergence extends from ${\displaystyle H_{\varepsilon }}$ to ${\displaystyle \Delta ^{2}}$. Looking at this from the perspective of the Reinhardt domain, ${\displaystyle H_{\varepsilon }}$ is the Reinhardt domain containing the center z = 0, and the domain of convergence of ${\displaystyle H_{\varepsilon }}$ has been extended to the smallest complete Reinhardt domain ${\displaystyle \Delta ^{2}}$ containing ${\displaystyle H_{\varepsilon }}$.^[24]

Thullen's^[25] classical result says that a 2-dimensional bounded Reinhard domain containing the origin is biholomorphic to one of the following domains provided that the orbit of the origin by the automorphism group has positive dimension:

1. ${\displaystyle \{(z,w)\in \mathbb {C} ^{2};~|z|<1,~|w|<1\}}$ (polydisc);
2. ${\displaystyle \{(z,w)\in \mathbb {C} ^{2};~|z|^{2}+|w|^{2}<1\}}$ (unit ball);
3. ${\displaystyle \{(z,w)\in \mathbb {C} ^{2};~|z|^{2}+|w|^{\frac {2}{p}}<1\}\,(p>0,\neq 1)}$ (Thullen domain).

Toshikazu Sunada (1978)^[26] established a generalization of Thullen's result:

Two n-dimensional bounded Reinhardt domains ${\displaystyle G_{1}}$ and ${\displaystyle G_{2}}$ are mutually biholomorphic if and only if there exists a transformation ${\displaystyle \varphi :\mathbb {C} ^{n}\to \mathbb {C} ^{n}}$ given by ${\displaystyle z_{i}\mapsto r_{i}z_{\sigma (i)}(r_{i}>0)}$, ${\displaystyle \sigma }$ being a permutation of the indices), such that ${\displaystyle \varphi (G_{1})=G_{2}}$.

When moving from the theory of one complex variable to the theory of several complex variables, depending on the range of the domain, it may not be possible to define a holomorphic function such that the boundary of the domain becomes a natural boundary. Considering the domain where the boundaries of the domain are natural boundaries (In the complex coordinate space ${\displaystyle \mathbb {C} ^{n}}$ call the domain of holomorphy), the first result of the domain of holomorphy was the holomorphic convexity of H. Cartan and Thullen.^[27] Levi's problem shows that the pseudoconvex domain was a domain of holomorphy. (First for ${\displaystyle \mathbb {C} ^{2}}$,^[28] later extended to ${\displaystyle \mathbb {C} ^{n}}$.^[29][30])^[31] Kiyoshi Oka's^[34][35] notion of idéal de domaines indéterminés is interpreted theory of sheaf cohomology by H. Cartan and more development Serre.^{[note 10][36][37][38][39][40][41][6]} In sheaf cohomology, the domain of holomorphy has come to be interpreted as the theory of Stein manifolds.^[42] The notion of the domain of holomorphy is also considered in other complex manifolds, furthermore also the complex analytic space which is its generalization.^[4]

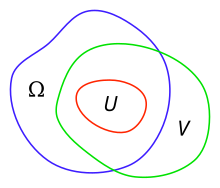
When a function f is holomorpic on the domain ${\displaystyle D\subset \mathbb {C} ^{n}}$ and cannot directly connect to the domain outside D, including the point of the domain boundary ${\displaystyle \partial D}$, the domain D is called the domain of holomorphy of f and the boundary is called the natural boundary of f. In other words, the domain of holomorphy D is the supremum of the domain where the holomorphic function f is holomorphic, and the domain D, which is holomorphic, cannot be extended any more. For several complex variables, i.e. domain ${\displaystyle D\subset \mathbb {C} ^{n}\ (n\geq 2)}$, the boundaries may not be natural boundaries. Hartogs' extension theorem gives an example of a domain where boundaries are not natural boundaries.^[43]

Formally, a domain D in the n-dimensional complex coordinate space ${\displaystyle \mathbb {C} ^{n}}$ is called a domain of holomorphy if there do not exist non-empty domain ${\displaystyle U\subset D}$ and ${\displaystyle V\subset \mathbb {C} ^{n}}$, ${\displaystyle V\not \subset D}$ and ${\displaystyle U\subset D\cap V}$ such that for every holomorphic function f on D there exists a holomorphic function g on V with ${\displaystyle f=g}$ on U.

For the ${\displaystyle n=1}$ case, the every domain (${\displaystyle D\subset \mathbb {C} }$) was the domain of holomorphy; we can define a holomorphic function with zeros accumulating everywhere on the boundary of the domain, which must then be a natural boundary for a domain of definition of its reciprocal.

• If ${\displaystyle D_{1},\dots ,D_{n}}$ are domains of holomorphy, then their intersection ${\textstyle D=\bigcap _{\nu =1}^{n}D_{\nu }}$ is also a domain of holomorphy.
• If ${\displaystyle D_{1}\subseteq D_{2}\subseteq \cdots }$ is an increasing sequence of domains of holomorphy, then their union ${\textstyle D=\bigcup _{n=1}^{\infty }D_{n}}$ is also a domain of holomorphy (see Behnke–Stein theorem).^[44]
• If ${\displaystyle D_{1}}$ and ${\displaystyle D_{2}}$ are domains of holomorphy, then ${\displaystyle D_{1}\times D_{2}}$ is a domain of holomorphy.
• The first Cousin problem is always solvable in a domain of holomorphy, also Cartan showed that the converse of this result was incorrect for ${\displaystyle n\geq 3}$.^[45] this is also true, with additional topological assumptions, for the second Cousin problem.

Let ${\displaystyle G\subset \mathbb {C} ^{n}}$ be a domain, or alternatively for a more general definition, let ${\displaystyle G}$ be an ${\displaystyle n}$ dimensional complex analytic manifold. Further let ${\displaystyle {\mathcal {O}}(G)}$ stand for the set of holomorphic functions on G. For a compact set ${\displaystyle K\subset G}$, the holomorphically convex hull of K is

${\displaystyle {\hat {K}}_{G}:=\left\{z\in G;|f(z)|\leq \sup _{w\in K}|f(w)|{\text{ for all }}f\in {\mathcal {O}}(G).\right\}.}$

One obtains a narrower concept of polynomially convex hull by taking ${\displaystyle {\mathcal {O}}(G)}$ instead to be the set of complex-valued polynomial functions on G. The polynomially convex hull contains the holomorphically convex hull.

The domain ${\displaystyle G}$ is called holomorphically convex if for every compact subset ${\displaystyle K,{\hat {K}}_{G}}$ is also compact in G. Sometimes this is just abbreviated as holomorph-convex.

When ${\displaystyle n=1}$, every domain ${\displaystyle G}$ is holomorphically convex since then ${\displaystyle {\hat {K}}_{G}}$ is the union of K with the relatively compact components of ${\displaystyle G\setminus K\subset G}$.

When ${\displaystyle n\geq 1}$, if f satisfies the above holomorphic convexity on D it has the following properties. ${\displaystyle {\text{dist}}(K,D^{c})={\text{dist}}({\hat {K}}_{D},D^{c})}$ for every compact subset K in D, where ${\displaystyle {\text{dist}}(K,D^{c})}$ denotes the distance between K and ${\displaystyle D^{c}=\mathbb {C} ^{n}\setminus D}$. Also, at this time, D is a domain of holomorphy. Therefore, every convex domain ${\displaystyle (D\subset \mathbb {C} ^{n})}$ is domain of holomorphy.^[5]

Hartogs showed that

Hartogs (1906):^[19] Let D be a Hartogs's domain on ${\displaystyle \mathbb {C} }$ and R be a positive function on D such that the set ${\displaystyle \Omega }$ in ${\displaystyle \mathbb {C} ^{2}}$ defined by ${\displaystyle z_{1}\in D}$ and ${\displaystyle |z_{2}|<R(z_{1})}$ is a domain of holomorphy. Then ${\displaystyle -\log {R}(z_{1})}$ is a subharmonic function on D.^[4]

If such a relations holds in the domain of holomorphy of several complex variables, it looks like a more manageable condition than a holomorphically convex.^{[note 11]} The subharmonic function looks like a kind of convex function, so it was named by Levi as a pseudoconvex domain (Hartogs's pseudoconvexity). Pseudoconvex domain (boundary of pseudoconvexity) are important, as they allow for classification of domains of holomorphy. A domain of holomorphy is a global property, by contrast, pseudoconvexity is that local analytic or local geometric property of the boundary of a domain.^[46]

A function

${\displaystyle f\colon D\to {\mathbb {R} }\cup \{-\infty \},}$

with domain ${\displaystyle D\subset {\mathbb {C} }^{n}}$

is called plurisubharmonic if it is upper semi-continuous, and for every complex line

${\displaystyle \{a+bz;z\in \mathbb {C} \}\subset \mathbb {C} ^{n}}$ with ${\displaystyle a,b\in \mathbb {C} ^{n}}$

the function ${\displaystyle z\mapsto f(a+bz)}$ is a subharmonic function on the set

${\displaystyle \{z\in \mathbb {C} ;a+bz\in D\}.}$

In full generality, the notion can be defined on an arbitrary complex manifold or even a Complex analytic space ${\displaystyle X}$ as follows. An upper semi-continuous function

${\displaystyle f\colon X\to \mathbb {R} \cup \{-\infty \}}$

is said to be plurisubharmonic if and only if for any holomorphic map

${\displaystyle \varphi \colon \Delta \to X}$ the function

${\displaystyle f\circ \varphi \colon \Delta \to \mathbb {R} \cup \{-\infty \}}$

is subharmonic, where ${\displaystyle \Delta \subset \mathbb {C} }$ denotes the unit disk.

In one-complex variable, necessary and sufficient condition that the real-valued function ${\displaystyle u=u(z)}$, that can be second-order differentiable with respect to z of one-variable complex function is subharmonic is ${\displaystyle \Delta =4\left({\frac {\partial ^{2}u}{\partial z\,\partial {\overline {z}}}}\right)\geq 0}$. Therefore, if ${\displaystyle u}$ is of class ${\displaystyle {\mathcal {C}}^{2}}$, then ${\displaystyle u}$ is plurisubharmonic if and only if the hermitian matrix ${\displaystyle H_{u}=(\lambda _{ij}),\lambda _{ij}={\frac {\partial ^{2}u}{\partial z_{i}\,\partial {\bar {z}}_{j}}}}$ is positive semidefinite.

Equivalently, a ${\displaystyle {\mathcal {C}}^{2}}$-function u is plurisubharmonic if and only if ${\displaystyle {\sqrt {-1}}\partial {\bar {\partial }}f}$ is a positive (1,1)-form.^{[47]: 39–40}

When the hermitian matrix of u is positive-definite and class ${\displaystyle {\mathcal {C}}^{2}}$, we call u a strict plurisubharmonic function.

Weak pseudoconvex is defined as : Let ${\displaystyle X\subset {\mathbb {C} }^{n}}$ be a domain. One says that X is pseudoconvex if there exists a continuous plurisubharmonic function ${\displaystyle \varphi }$ on X such that the set ${\displaystyle \{z\in X;\varphi (z)\leq \sup x\}}$ is a relatively compact subset of X for all real numbers x. ^{[note 12]} i.e. there exists a smooth plurisubharmonic exhaustion function ${\displaystyle \psi \in {\text{Psh}}(X)\cap {\mathcal {C}}^{\infty }(X)}$. Often, the definition of pseudoconvex is used here and is written as; Let X be a complex n-dimensional manifold. Then is said to be weeak pseudoconvex there exists a smooth plurisubharmonic exhaustion function ${\displaystyle \psi \in {\text{Psh}}(X)\cap {\mathcal {C}}^{\infty }(X)}$.^[47]: 49

Let X be a complex n-dimensional manifold. Strongly (or Strictly) pseudoconvex if there exists a smooth strictly plurisubharmonic exhaustion function ${\displaystyle \psi \in {\text{Psh}}(X)\cap {\mathcal {C}}^{\infty }(X)}$, i.e., ${\displaystyle H\psi }$ is positive definite at every point. The strongly pseudoconvex domain is the pseudoconvex domain.^[47]: 49 Strongly pseudoconvex and strictly pseudoconvex (i.e. 1-convex and 1-complete^[48]) are often used interchangeably,^[49] see Lempert^[50] for the technical difference.

If ${\displaystyle {\mathcal {C}}^{2}}$ boundary , it can be shown that D has a defining function; i.e., that there exists ${\displaystyle \rho :\mathbb {C} ^{n}\to \mathbb {R} }$ which is ${\displaystyle {\mathcal {C}}^{2}}$ so that ${\displaystyle D=\{\rho <0\}}$, and ${\displaystyle \partial D=\{\rho =0\}}$. Now, D is pseudoconvex iff for every ${\displaystyle p\in \partial D}$ and ${\displaystyle w}$ in the complex tangent space at p, that is,

${\displaystyle \nabla \rho (p)w=\sum _{i=1}^{n}{\frac {\partial \rho (p)}{\partial z_{j}}}w_{j}=0}$, we have

${\displaystyle H(\rho )=\sum _{i,j=1}^{n}{\frac {\partial ^{2}\rho (p)}{\partial z_{i}\,\partial {\bar {z_{j}}}}}w_{i}{\bar {w_{j}}}\geq 0.}$^[5][51]

If D does not have a ${\displaystyle {\mathcal {C}}^{2}}$ boundary, the following approximation result can be useful.

Proposition 1 If D is pseudoconvex, then there exist bounded, strongly Levi pseudoconvex domains ${\displaystyle D_{k}\subset D}$ with class ${\displaystyle {\mathcal {C}}^{\infty }}$-boundary which are relatively compact in D, such that

${\displaystyle D=\bigcup _{k=1}^{\infty }D_{k}.}$

This is because once we have a ${\displaystyle \varphi }$ as in the definition we can actually find a ${\displaystyle {\mathcal {C}}^{\infty }}$ exhaustion function.

When the Levi (–Krzoska) form is positive-definite, it is called strongly Levi (–Krzoska) pseudoconvex or often called simply strongly (or strictly) pseudoconvex.^[5]

If for every boundary point ${\displaystyle \rho }$ of D, there exists an analytic variety ${\displaystyle {\mathcal {B}}}$ passing ${\displaystyle \rho }$ which lies entirely outside D in some neighborhood around ${\displaystyle \rho }$, except the point ${\displaystyle \rho }$ itself. Domain D that satisfies these conditions is called Levi total pseudoconvex.^[52]

Let n-functions ${\displaystyle \varphi :z_{j}=\varphi _{j}(u,t)}$ be continuous on ${\displaystyle \Delta :|U|\leq 1,0\leq t\leq 1}$, holomorphic in ${\displaystyle |u|<1}$ when the parameter t is fixed in [0, 1], and assume that ${\displaystyle {\frac {\partial \varphi _{j}}{\partial u}}}$ are not all zero at any point on ${\displaystyle \Delta }$. Then the set ${\displaystyle Q(t):=\{Z_{j}=\varphi _{j}(u,t);|u|\leq 1\}}$ is called an analytic disc de-pending on a parameter t, and ${\displaystyle B(t):=\{Z_{j}=\varphi _{j}(u,t);|u|=1\}}$ is called its shell. If ${\displaystyle Q(t)\subset D\ (0<t)}$ and ${\displaystyle B(0)\subset D}$, Q(t) is called Family of Oka's disk.^[52][53]

When ${\displaystyle Q(0)\subset D}$ holds on any family of Oka's disk, D is called Oka pseudoconvex.^[52] Oka's proof of Levi's problem was that when the unramified Riemann domain over ${\displaystyle \mathbb {C} ^{n}}$^[54] was a domain of holomorphy (holomorphically convex), it was proved that it was necessary and sufficient that each boundary point of the domain of holomorphy is an Oka pseudoconvex.^[29][53]

For every point ${\displaystyle x\in \partial D}$ there exist a neighbourhood U of x and f holomorphic. ( i.e. ${\displaystyle U\cap D}$ be holomorphically convex.) such that f cannot be extended to any neighbourhood of x. i.e., let ${\displaystyle \psi :X\to Y}$ be a holomorphic map, if every point ${\displaystyle y\in Y}$ has a neighborhood U such that ${\displaystyle \psi ^{-1}(U)}$ admits a ${\displaystyle {\mathcal {C}}^{\infty }}$-plurisubharmonic exhaustion function (weakly 1-complete^[55]), in this situation, we call that X is locally pseudoconvex (or locally Stein) over Y. As an old name, it is also called Cartan pseudoconvex. In ${\displaystyle \mathbb {C} ^{n}}$ the locally pseudoconvex domain is itself a pseudoconvex domain and it is a domain of holomorphy.^[56][52] For example, Diederich–Fornæss^[57] found local pseudoconvex bounded domains ${\displaystyle \Omega }$ with smooth boundary on non-Kähler manifolds such that ${\displaystyle \Omega }$ is not weakly 1-complete.^{[58][note 13]}

For a domain ${\displaystyle D\subset \mathbb {C} ^{n}}$ the following conditions are equivalent:^{[note 14]}

1. D is a domain of holomorphy.
2. D is holomorphically convex.
3. D is the union of an increasing sequence of analytic polyhedrons in D.
4. D is pseudoconvex.
5. D is Locally pseudoconvex.

The implications ${\displaystyle 1\Leftrightarrow 2\Leftrightarrow 3}$,^{[note 15]} ${\displaystyle 1\Rightarrow 4}$,^{[note 16]} and ${\displaystyle 4\Rightarrow 5}$ are standard results. Proving ${\displaystyle 5\Rightarrow 1}$, i.e. constructing a global holomorphic function which admits no extension from non-extendable functions defined only locally. This is called the Levi problem (after E. E. Levi) and was solved for unramified Riemann domains over ${\displaystyle \mathbb {C} ^{n}}$ by Kiyoshi Oka,^{[note 17]} but for ramified Riemann domains, pseudoconvexity does not characterize holomorphically convexity,^[66] and then by Lars Hörmander using methods from functional analysis and partial differential equations (a consequence of ${\displaystyle {\bar {\partial }}}$-problem(equation) with a L² methods).^{[1][43][3][67]}

The introduction of sheaves into several complex variables allowed the reformulation of and solution to several important problems in the field.

Oka introduced the notion which he termed "idéal de domaines indéterminés" or "ideal of indeterminate domains".^[34][35] Specifically, it is a set ${\displaystyle (I)}$ of pairs ${\displaystyle (f,\delta )}$, ${\displaystyle f}$ holomorphic on a non-empty open set ${\displaystyle \delta }$, such that

1. If ${\displaystyle (f,\delta )\in (I)}$ and ${\displaystyle (a,\delta ')}$ is arbitrary, then ${\displaystyle (af,\delta \cap \delta ')\in (I)}$.
2. For each ${\displaystyle (f,\delta ),(f',\delta ')\in (I)}$, then ${\displaystyle (f+f',\delta \cap \delta ')\in (I).}$

The origin of indeterminate domains comes from the fact that domains change depending on the pair ${\displaystyle (f,\delta )}$. Cartan^[36][37] translated this notion into the notion of the coherent (sheaf) (Especially, coherent analytic sheaf) in sheaf cohomology.^[67][68] This name comes from H. Cartan.^[69] Also, Serre (1955) introduced the notion of the coherent sheaf into algebraic geometry, that is, the notion of the coherent algebraic sheaf.^[70] The notion of coherent (coherent sheaf cohomology) helped solve the problems in several complex variables.^[39]

The definition of the coherent sheaf is as follows.^{[70][71][72][73] [47]: 83–89} A quasi-coherent sheaf on a ringed space ${\displaystyle (X,{\mathcal {O}}_{X})}$ is a sheaf ${\displaystyle {\mathcal {F}}}$ of ${\displaystyle {\mathcal {O}}_{X}}$-modules which has a local presentation, that is, every point in ${\displaystyle X}$ has an open neighborhood ${\displaystyle U}$ in which there is an exact sequence

${\displaystyle {\mathcal {O}}_{X}^{\oplus I}|_{U}\to {\mathcal {O}}_{X}^{\oplus J}|_{U}\to {\mathcal {F}}|_{U}\to 0}$

for some (possibly infinite) sets ${\displaystyle I}$ and ${\displaystyle J}$.

A coherent sheaf on a ringed space ${\displaystyle (X,{\mathcal {O}}_{X})}$ is a sheaf ${\displaystyle {\mathcal {F}}}$ satisfying the following two properties:

1. ${\displaystyle {\mathcal {F}}}$ is of finite type over ${\displaystyle {\mathcal {O}}_{X}}$, that is, every point in ${\displaystyle X}$ has an open neighborhood ${\displaystyle U}$ in ${\displaystyle X}$ such that there is a surjective morphism ${\displaystyle {\mathcal {O}}_{X}^{\oplus n}|_{U}\to {\mathcal {F}}|_{U}}$ for some natural number ${\displaystyle n}$;
2. for each open set ${\displaystyle U\subseteq X}$, integer ${\displaystyle n>0}$, and arbitrary morphism ${\displaystyle \varphi :{\mathcal {O}}_{X}^{\oplus n}|_{U}\to {\mathcal {F}}|_{U}}$ of ${\displaystyle {\mathcal {O}}_{X}}$-modules, the kernel of ${\displaystyle \varphi }$ is of finite type.

Morphisms between (quasi-)coherent sheaves are the same as morphisms of sheaves of ${\displaystyle {\mathcal {O}}_{X}}$-modules.

Also, Jean-Pierre Serre (1955)^[70] proves that

If in an exact sequence ${\displaystyle 0\to {\mathcal {F}}_{1}|_{U}\to {\mathcal {F}}_{2}|_{U}\to {\mathcal {F}}_{3}|_{U}\to 0}$ of sheaves of ${\displaystyle {\mathcal {O}}}$-modules two of the three sheaves ${\displaystyle {\mathcal {F}}_{j}}$ are coherent, then the third is coherent as well.

(Oka–Cartan) coherent theorem^[34] says that each sheaf that meets the following conditions is a coherent.^[74]

1. the sheaf ${\displaystyle {\mathcal {O}}:={\mathcal {O}}_{\mathbb {C} _{n}}}$ of germs of holomorphic functions on ${\displaystyle \mathbb {C} _{n}}$, or the structure sheaf