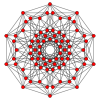
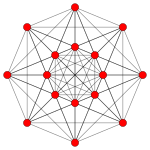
Uniform 5-polytope
In geometry, a uniform 5-polytope is a five-dimensional uniform polytope. By definition, a uniform 5-polytope is vertex-transitive and constructed from uniform 4-polytope facets.
The complete set of convex uniform 5-polytopes has not been determined, but many can be made as Wythoff constructions from a small set of symmetry groups. These construction operations are represented by the permutations of rings of the Coxeter diagrams.
History of discovery
[edit]- Regular polytopes: (convex faces)
- 1852: Ludwig Schläfli proved in his manuscript Theorie der vielfachen Kontinuität that there are exactly 3 regular polytopes in 5 or more dimensions.
- Convex semiregular polytopes: (Various definitions before Coxeter's uniform category)
- 1900: Thorold Gosset enumerated the list of nonprismatic semiregular convex polytopes with regular facets (convex regular 4-polytopes) in his publication On the Regular and Semi-Regular Figures in Space of n Dimensions.[1]
- Convex uniform polytopes:
- 1940-1988: The search was expanded systematically by H.S.M. Coxeter in his publication Regular and Semi-Regular Polytopes I, II, and III.
- 1966: Norman W. Johnson completed his Ph.D. Dissertation under Coxeter, The Theory of Uniform Polytopes and Honeycombs, University of Toronto
- Non-convex uniform polytopes:
- 1966: Johnson describes two non-convex uniform antiprisms in 5-space in his dissertation.[2]
- 2000-2024: Jonathan Bowers and other researchers search for other non-convex uniform 5-polytopes,[3] with a current count of 1348 known uniform 5-polytopes outside infinite families (convex and non-convex), excluding the prisms of the uniform 4-polytopes. The list is not proven complete.[4][5]
Regular 5-polytopes
[edit]Regular 5-polytopes can be represented by the Schläfli symbol {p,q,r,s}, with s {p,q,r} 4-polytope facets around each face. There are exactly three such regular polytopes, all convex:
- {3,3,3,3} - 5-simplex
- {4,3,3,3} - 5-cube
- {3,3,3,4} - 5-orthoplex
There are no nonconvex regular polytopes in 5 dimensions or above.
Convex uniform 5-polytopes
[edit]There are 104 known convex uniform 5-polytopes, plus a number of infinite families of duoprism prisms, and polygon-polyhedron duoprisms. All except the grand antiprism prism are based on Wythoff constructions, reflection symmetry generated with Coxeter groups.[citation needed]
Symmetry of uniform 5-polytopes in four dimensions
[edit]The 5-simplex is the regular form in the A5 family. The 5-cube and 5-orthoplex are the regular forms in the B5 family. The bifurcating graph of the D5 family contains the 5-orthoplex, as well as a 5-demicube which is an alternated 5-cube.
Each reflective uniform 5-polytope can be constructed in one or more reflective point group in 5 dimensions by a Wythoff construction, represented by rings around permutations of nodes in a Coxeter diagram. Mirror hyperplanes can be grouped, as seen by colored nodes, separated by even-branches. Symmetry groups of the form [a,b,b,a], have an extended symmetry, [[a,b,b,a]], like [3,3,3,3], doubling the symmetry order. Uniform polytopes in these group with symmetric rings contain this extended symmetry.
If all mirrors of a given color are unringed (inactive) in a given uniform polytope, it will have a lower symmetry construction by removing all of the inactive mirrors. If all the nodes of a given color are ringed (active), an alternation operation can generate a new 5-polytope with chiral symmetry, shown as "empty" circled nodes", but the geometry is not generally adjustable to create uniform solutions.

- Fundamental families[7]
| Group symbol | Order | Coxeter graph | Bracket notation | Commutator subgroup | Coxeter number (h) | Reflections m=5/2 h[8] | ||
|---|---|---|---|---|---|---|---|---|
| A5 | 720 | [3,3,3,3] | [3,3,3,3]+ | 6 | 15 | |||
| D5 | 1920 | [3,3,31,1] | [3,3,31,1]+ | 8 | 20 | |||
| B5 | 3840 | [4,3,3,3] | 10 | 5 | 20 | |||
- Uniform prisms
There are 5 finite categorical uniform prismatic families of polytopes based on the nonprismatic uniform 4-polytopes. There is one infinite family of 5-polytopes based on prisms of the uniform duoprisms {p}×{q}×{ }.
| Coxeter group | Order | Coxeter diagram | Coxeter notation | Commutator subgroup | Reflections | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| A4A1 | 120 | [3,3,3,2] = [3,3,3]×[ ] | [3,3,3]+ | 10 | 1 | ||||||
| D4A1 | 384 | [31,1,1,2] = [31,1,1]×[ ] | [31,1,1]+ | 12 | 1 | ||||||
| B4A1 | 768 | [4,3,3,2] = [4,3,3]×[ ] | 4 | 12 | 1 | ||||||
| F4A1 | 2304 | [3,4,3,2] = [3,4,3]×[ ] | [3+,4,3+] | 12 | 12 | 1 | |||||
| H4A1 | 28800 | [5,3,3,2] = [3,4,3]×[ ] | [5,3,3]+ | 60 | 1 | ||||||
| Duoprismatic prisms (use 2p and 2q for evens) | |||||||||||
| I2(p)I2(q)A1 | 8pq | [p,2,q,2] = [p]×[q]×[ ] | [p+,2,q+] | p | q | 1 | |||||
| I2(2p)I2(q)A1 | 16pq | [2p,2,q,2] = [2p]×[q]×[ ] | p | p | q | 1 | |||||
| I2(2p)I2(2q)A1 | 32pq | [2p,2,2q,2] = [2p]×[2q]×[ ] | p | p | q | q | 1 | ||||
- Uniform duoprisms
There are 3 categorical uniform duoprismatic families of polytopes based on Cartesian products of the uniform polyhedra and regular polygons: {q,r}×{p}.
| Coxeter group | Order | Coxeter diagram | Coxeter notation | Commutator subgroup | Reflections | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Prismatic groups (use 2p for even) | |||||||||||
| A3I2(p) | 48p | [3,3,2,p] = [3,3]×[p] | [(3,3)+,2,p+] | 6 | p | ||||||
| A3I2(2p) | 96p | [3,3,2,2p] = [3,3]×[2p] | 6 | p | p | ||||||
| B3I2(p) | 96p | [4,3,2,p] = [4,3]×[p] | 3 | 6 | p | ||||||
| B3I2(2p) | 192p | [4,3,2,2p] = [4,3]×[2p] | 3 | 6 | p | p | |||||
| H3I2(p) | 240p | [5,3,2,p] = [5,3]×[p] | [(5,3)+,2,p+] | 15 | p | ||||||
| H3I2(2p) | 480p | [5,3,2,2p] = [5,3]×[2p] | 15 | p | p | ||||||
Enumerating the convex uniform 5-polytopes
[edit]- Simplex family: A5 [34]
- 19 uniform 5-polytopes
- Hypercube/Orthoplex family: B5 [4,33]
- 31 uniform 5-polytopes
- Demihypercube D5/E5 family: [32,1,1]
- 23 uniform 5-polytopes (8 unique)
- Polychoral prisms:
- 56 uniform 5-polytope (45 unique) constructions based on prismatic families: [3,3,3]×[ ], [4,3,3]×[ ], [5,3,3]×[ ], [31,1,1]×[ ].
- One non-Wythoffian - The grand antiprism prism is the only known non-Wythoffian convex uniform 5-polytope, constructed from two grand antiprisms connected by polyhedral prisms.
That brings the tally to: 19+31+8+45+1=104
In addition there are:
- Infinitely many uniform 5-polytope constructions based on duoprism prismatic families: [p]×[q]×[ ].
- Infinitely many uniform 5-polytope constructions based on duoprismatic families: [3,3]×[p], [4,3]×[p], [5,3]×[p].
The A5 family
[edit]There are 19 forms based on all permutations of the Coxeter diagrams with one or more rings. (16+4-1 cases)
They are named by Norman Johnson from the Wythoff construction operations upon regular 5-simplex (hexateron).
The A5 family has symmetry of order 720 (6 factorial). 7 of the 19 figures, with symmetrically ringed Coxeter diagrams have doubled symmetry, order 1440.
The coordinates of uniform 5-polytopes with 5-simplex symmetry can be generated as permutations of simple integers in 6-space, all in hyperplanes with normal vector (1,1,1,1,1,1).
| # | Base point | Johnson naming system Bowers name and (acronym) Coxeter diagram | k-face element counts | Vertex figure | Facet counts by location: [3,3,3,3] | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 4 | 3 | 2 | 1 | 0 | [3,3,3] (6) | [3,3,2] (15) | [3,2,3] (20) | [2,3,3] (15) | [3,3,3] (6) | Alt | ||||
| 1 | (0,0,0,0,0,1) or (0,1,1,1,1,1) | 5-simplex hexateron (hix) | 6 | 15 | 20 | 15 | 6 | 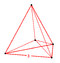 {3,3,3} |  {3,3,3} | - | - | - | - | |
| 2 | (0,0,0,0,1,1) or (0,0,1,1,1,1) | Rectified 5-simplex rectified hexateron (rix) | 12 | 45 | 80 | 60 | 15 |  t{3,3}×{ } |  r{3,3,3} | - | - | - |  {3,3,3} | |
| 3 | (0,0,0,0,1,2) or (0,1,2,2,2,2) | Truncated 5-simplex truncated hexateron (tix) | 12 | 45 | 80 | 75 | 30 |  Tetrah.pyr |  t{3,3,3} | - | - | - |  {3,3,3} | |
| 4 | (0,0,0,1,1,2) or (0,1,1,2,2,2) | Cantellated 5-simplex small rhombated hexateron (sarx) | 27 | 135 | 290 | 240 | 60 | prism-wedge |  rr{3,3,3} | - | - |  { }×{3,3} |  r{3,3,3} | |
| 5 | (0,0,0,1,2,2) or (0,0,1,2,2,2) | Bitruncated 5-simplex bitruncated hexateron (bittix) | 12 | 60 | 140 | 150 | 60 |  |  2t{3,3,3} | - | - | - |  t{3,3,3} | |
| 6 | (0,0,0,1,2,3) or (0,1,2,3,3,3) | Cantitruncated 5-simplex great rhombated hexateron (garx) | 27 | 135 | 290 | 300 | 120 | 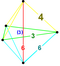 | 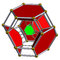 tr{3,3,3} | - | - |  { }×{3,3} |  t{3,3,3} | |
| 7 | (0,0,1,1,1,2) or (0,1,1,1,2,2) | Runcinated 5-simplex small prismated hexateron (spix) | 47 | 255 | 420 | 270 | 60 |  |  t0,3{3,3,3} | - |  {3}×{3} |  { }×r{3,3} |  r{3,3,3} | |
| 8 | (0,0,1,1,2,3) or (0,1,2,2,3,3) | Runcitruncated 5-simplex prismatotruncated hexateron (pattix) | 47 | 315 | 720 | 630 | 180 | 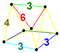 | 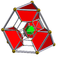 t0,1,3{3,3,3} | - |  {6}×{3} |  { }×r{3,3} |  rr{3,3,3} | |
| 9 | (0,0,1,2,2,3) or (0,1,1,2,3,3) | Runcicantellated 5-simplex prismatorhombated hexateron (pirx) | 47 | 255 | 570 | 540 | 180 | 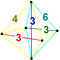 |  t0,1,3{3,3,3} | - |  {3}×{3} |  { }×t{3,3} |  2t{3,3,3} | |
| 10 | (0,0,1,2,3,4) or (0,1,2,3,4,4) | Runcicantitruncated 5-simplex great prismated hexateron (gippix) | 47 | 315 | 810 | 900 | 360 |  Irr.5-cell |  t0,1,2,3{3,3,3} | - |  {3}×{6} |  { }×t{3,3} |  tr{3,3,3} | |
| 11 | (0,1,1,1,2,3) or (0,1,2,2,2,3) | Steritruncated 5-simplex celliprismated hexateron (cappix) | 62 | 330 | 570 | 420 | 120 |  |  t{3,3,3} |  { }×t{3,3} |  {3}×{6} |  { }×{3,3} |  t0,3{3,3,3} | |
| 12 | (0,1,1,2,3,4) or (0,1,2,3,3,4) | Stericantitruncated 5-simplex celligreatorhombated hexateron (cograx) | 62 | 480 | 1140 | 1080 | 360 |  tr{3,3,3} |  { }×tr{3,3} |  {3}×{6} |  { }×rr{3,3} |  t0,1,3{3,3,3} | ||
| 13 | (0,0,0,1,1,1) | Birectified 5-simplex dodecateron (dot) | 12 | 60 | 120 | 90 | 20 |  {3}×{3} |  r{3,3,3} | - | - | - |  r{3,3,3} | |
| 14 | (0,0,1,1,2,2) | Bicantellated 5-simplex small birhombated dodecateron (sibrid) | 32 | 180 | 420 | 360 | 90 |  |  rr{3,3,3} | - |  {3}×{3} | - |  rr{3,3,3} | |
| 15 | (0,0,1,2,3,3) | Bicantitruncated 5-simplex great birhombated dodecateron (gibrid) | 32 | 180 | 420 | 450 | 180 |  |  tr{3,3,3} | - |  {3}×{3} | - |  tr{3,3,3} | |
| 16 | (0,1,1,1,1,2) | Stericated 5-simplex small cellated dodecateron (scad) | 62 | 180 | 210 | 120 | 30 |  Irr.16-cell |  {3,3,3} |  { }×{3,3} |  {3}×{3} |  { }×{3,3} |  {3,3,3} | |
| 17 | (0,1,1,2,2,3) | Stericantellated 5-simplex small cellirhombated dodecateron (card) | 62 | 420 | 900 | 720 | 180 |  |  rr{3,3,3} |  { }×rr{3,3} |  {3}×{3} |  { }×rr{3,3} |  rr{3,3,3} | |
| 18 | (0,1,2,2,3,4) | Steriruncitruncated 5-simplex celliprismatotruncated dodecateron (captid) | 62 | 450 | 1110 | 1080 | 360 |  t0,1,3{3,3,3} |  { }×t{3,3} |  {6}×{6} |  { }×t{3,3} |  t0,1,3{3,3,3} | ||
| 19 | (0,1,2,3,4,5) | Omnitruncated 5-simplex great cellated dodecateron (gocad) | 62 | 540 | 1560 | 1800 | 720 |  Irr. {3,3,3} |  t0,1,2,3{3,3,3} |  { }×tr{3,3} |  {6}×{6} |  { }×tr{3,3} |  t0,1,2,3{3,3,3} | |
| Nonuniform | Omnisnub 5-simplex snub dodecateron (snod) snub hexateron (snix) | 422 | 2340 | 4080 | 2520 | 360 | ht0,1,2,3{3,3,3} | ht0,1,2,3{3,3,2} | ht0,1,2,3{3,2,3} | ht0,1,2,3{3,3,2} | ht0,1,2,3{3,3,3} | (360) Irr. {3,3,3} | ||
The B5 family
[edit]The B5 family has symmetry of order 3840 (5!×25).
This family has 25−1=31 Wythoffian uniform polytopes generated by marking one or more nodes of the Coxeter diagram. Also added are 8 uniform polytopes generated as alternations with half the symmetry, which form a complete duplicate of the D5 family as ![]()
![]()
![]()
![]() ... =
... = ![]()
![]() ..... (There are more alternations that are not listed because they produce only repetitions, as
..... (There are more alternations that are not listed because they produce only repetitions, as ![]()
![]()
![]()
![]() ... =
... = ![]()
![]() .... and
.... and ![]()
![]()
![]()
![]() ... =
... = ![]()
![]() .... These would give a complete duplication of the uniform 5-polytopes numbered 20 through 34 with symmetry broken in half.)
.... These would give a complete duplication of the uniform 5-polytopes numbered 20 through 34 with symmetry broken in half.)
For simplicity it is divided into two subgroups, each with 12 forms, and 7 "middle" forms which equally belong in both.
The 5-cube family of 5-polytopes are given by the convex hulls of the base points listed in the following table, with all permutations of coordinates and sign taken. Each base point generates a distinct uniform 5-polytope. All coordinates correspond with uniform 5-polytopes of edge length 2.
| # | Base point | Name Coxeter diagram | Element counts | Vertex figure | Facet counts by location: [4,3,3,3] | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 4 | 3 | 2 | 1 | 0 | [4,3,3] (10) | [4,3,2] (40) | [4,2,3] (80) | [2,3,3] (80) | [3,3,3] (32) | Alt | ||||
| 20 | (0,0,0,0,1)√2 | 5-orthoplex triacontaditeron (tac) | 32 | 80 | 80 | 40 | 10 |  {3,3,4} | - | - | - | - |  {3,3,3} | |
| 21 | (0,0,0,1,1)√2 | Rectified 5-orthoplex rectified triacontaditeron (rat) | 42 | 240 | 400 | 240 | 40 |  { }×{3,4} |  {3,3,4} | - | - | - |  r{3,3,3} | |
| 22 | (0,0,0,1,2)√2 | Truncated 5-orthoplex truncated triacontaditeron (tot) | 42 | 240 | 400 | 280 | 80 |  (Octah.pyr) |  {3,3,4} | - | - | - |  t{3,3,3} | |
| 23 | (0,0,1,1,1)√2 | Birectified 5-cube penteractitriacontaditeron (nit) (Birectified 5-orthoplex) | 42 | 280 | 640 | 480 | 80 |  {4}×{3} |  r{3,3,4} | - | - | - |  r{3,3,3} | |
| 24 | (0,0,1,1,2)√2 | Cantellated 5-orthoplex small rhombated triacontaditeron (sart) | 82 | 640 | 1520 | 1200 | 240 |  Prism-wedge |  r{3,3,4} |  { }×{3,4} | - | - |  rr{3,3,3} | |
| 25 | (0,0,1,2,2)√2 | Bitruncated 5-orthoplex bitruncated triacontaditeron (bittit) | 42 | 280 | 720 | 720 | 240 |  |  t{3,3,4} | - | - | - |  2t{3,3,3} | |
| 26 | (0,0,1,2,3)√2 | Cantitruncated 5-orthoplex great rhombated triacontaditeron (gart) | 82 | 640 | 1520 | 1440 | 480 |  |  t{3,3,4} |  { }×{3,4} | - | - |  t0,1,3{3,3,3} | |
| 27 | (0,1,1,1,1)√2 | Rectified 5-cube rectified penteract (rin) | 42 | 200 | 400 | 320 | 80 |  {3,3}×{ } |  r{4,3,3} | - | - | - |  {3,3,3} | |
| 28 | (0,1,1,1,2)√2 | Runcinated 5-orthoplex small prismated triacontaditeron (spat) | 162 | 1200 | 2160 | 1440 | 320 |  |  r{4,3,3} |  { }×r{3,4} |  {3}×{4} |  t0,3{3,3,3} | ||
| 29 | (0,1,1,2,2)√2 | Bicantellated 5-cube small birhombated penteractitriacontaditeron (sibrant) (Bicantellated 5-orthoplex) | 122 | 840 | 2160 | 1920 | 480 |  |  rr{3,3,4} | - |  {4}×{3} | - |  rr{3,3,3} | |
| 30 | (0,1,1,2,3)√2 | Runcitruncated 5-orthoplex prismatotruncated triacontaditeron (pattit) | 162 | 1440 | 3680 | 3360 | 960 |  |  rr{3,3,4} |  { }×r{3,4} |  {6}×{4} | - |  t0,1,3{3,3,3} | |
| 31 | (0,1,2,2,2)√2 | Bitruncated 5-cube bitruncated penteract (bittin) | 42 | 280 | 720 | 800 | 320 |  |  2t{4,3,3} | - | - | - |  t{3,3,3} | |
| 32 | (0,1,2,2,3)√2 | Runcicantellated 5-orthoplex prismatorhombated triacontaditeron (pirt) | 162 | 1200 | 2960 | 2880 | 960 |  |  2t{4,3,3} |  { }×t{3,4} |  {3}×{4} | - |  t0,1,3{3,3,3} | |
| 33 | (0,1,2,3,3)√2 | Bicantitruncated 5-cube great birhombated triacontaditeron (gibrant) (Bicantitruncated 5-orthoplex) | 122 | 840 | 2160 | 2400 | 960 |  |  tr{3,3,4} | - |  {4}×{3} | - |  rr{3,3,3} | |
| 34 | (0,1,2,3,4)√2 | Runcicantitruncated 5-orthoplex great prismated triacontaditeron (gippit) | 162 | 1440 | 4160 | 4800 | 1920 |  |  tr{3,3,4} |  { }×t{3,4} |  {6}×{4} | - |  t0,1,2,3{3,3,3} | |
| 35 | (1,1,1,1,1) | 5-cube penteract (pent) | 10 | 40 | 80 | 80 | 32 |  {3,3,3} |  {4,3,3} | - | - | - | - | |
| 36 | (1,1,1,1,1) + (0,0,0,0,1)√2 | Stericated 5-cube small cellated penteractitriacontaditeron (scant) (Stericated 5-orthoplex) | 242 | 800 | 1040 | 640 | 160 |  Tetr.antiprm |  {4,3,3} |  {4,3}×{ } |  {4}×{3} |  { }×{3,3} |  {3,3,3} | |
| 37 | (1,1,1,1,1) + (0,0,0,1,1)√2 | Runcinated 5-cube small prismated penteract (span) | 202 | 1240 | 2160 | 1440 | 320 | 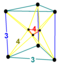 |  t0,3{4,3,3} | - |  {4}×{3} |  { }×r{3,3} |  r{3,3,3} | |
| 38 | (1,1,1,1,1) + (0,0,0,1,2)√2 | Steritruncated 5-orthoplex celliprismated triacontaditeron (cappin) | 242 | 1520 | 2880 | 2240 | 640 | 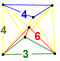 |  t0,3{4,3,3} |  {4,3}×{ } |  {6}×{4} |  { }×t{3,3} |  t{3,3,3} | |
| 39 | (1,1,1,1,1) + (0,0,1,1,1)√2 | Cantellated 5-cube small rhombated penteract (sirn) | 122 | 680 | 1520 | 1280 | 320 | Prism-wedge |  rr{4,3,3} | - | - |  { }×{3,3} |  r{3,3,3} | |
| 40 | (1,1,1,1,1) + (0,0,1,1,2)√2 | Stericantellated 5-cube cellirhombated penteractitriacontaditeron (carnit) (Stericantellated 5-orthoplex) | 242 | 2080 | 4720 | 3840 | 960 |  |  rr{4,3,3} | 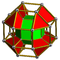 rr{4,3}×{ } |  {4}×{3} |  { }×rr{3,3} |  rr{3,3,3} | |
| 41 | (1,1,1,1,1) + (0,0,1,2,2)√2 | Runcicantellated 5-cube prismatorhombated penteract (prin) | 202 | 1240 | 2960 | 2880 | 960 |  |  t0,2,3{4,3,3} | - |  {4}×{3} |  { }×t{3,3} |  2t{3,3,3} | |
| 42 | (1,1,1,1,1) + (0,0,1,2,3)√2 | Stericantitruncated 5-orthoplex celligreatorhombated triacontaditeron (cogart) | 242 | 2320 | 5920 | 5760 | 1920 |  t0,2,3{4,3,3} |  rr{4,3}×{ } |  {6}×{4} |  { }×tr{3,3} |  tr{3,3,3} | ||
| 43 | (1,1,1,1,1) + (0,1,1,1,1)√2 | Truncated 5-cube truncated penteract (tan) | 42 | 200 | 400 | 400 | 160 | 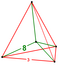 Tetrah.pyr |  t{4,3,3} | - | - | - |  {3,3,3} | |
| 44 | (1,1,1,1,1) + (0,1,1,1,2)√2 | Steritruncated 5-cube celliprismated triacontaditeron (capt) | 242 | 1600 | 2960 | 2240 | 640 |  |  t{4,3,3} |  t{4,3}×{ } |  {8}×{3} |  { }×{3,3} |  t0,3{3,3,3} | |
| 45 | (1,1,1,1,1) + (0,1,1,2,2)√2 | Runcitruncated 5-cube prismatotruncated penteract (pattin) | 202 | 1560 | 3760 | 3360 | 960 |  |  t0,1,3{4,3,3} | - |  {8}×{3} |  { }×r{3,3} |  rr{3,3,3} | |
| 46 | (1,1,1,1,1) + (0,1,1,2,3)√2 | Steriruncitruncated 5-cube celliprismatotruncated penteractitriacontaditeron (captint) (Steriruncitruncated 5-orthoplex) | 242 | 2160 | 5760 | 5760 | 1920 |  t0,1,3{4,3,3} |  t{4,3}×{ } |  {8}×{6} |  { }×t{3,3} |  t0,1,3{3,3,3} | ||
| 47 | (1,1,1,1,1) + (0,1,2,2,2)√2 | Cantitruncated 5-cube great rhombated penteract (girn) | 122 | 680 | 1520 | 1600 | 640 |  |  tr{4,3,3} | - | - |  { }×{3,3} |  t{3,3,3} | |
| 48 | (1,1,1,1,1) + (0,1,2,2,3)√2 | Stericantitruncated 5-cube celligreatorhombated penteract (cogrin) | 242 | 2400 | 6000 | 5760 | 1920 |  tr{4,3,3} |  tr{4,3}×{ } |  {8}×{3} |  { }×rr{3,3} |  t0,1,3{3,3,3} | ||
| 49 | (1,1,1,1,1) + (0,1,2,3,3)√2 | Runcicantitruncated 5-cube great prismated penteract (gippin) | 202 | 1560 | 4240 | 4800 | 1920 |  |  t0,1,2,3{4,3,3} | - |  {8}×{3} |  { }×t{3,3} |  tr{3,3,3} | |
| 50 | (1,1,1,1,1) + (0,1,2,3,4)√2 | Omnitruncated 5-cube great cellated penteractitriacontaditeron (gacnet) (omnitruncated 5-orthoplex) | 242 | 2640 | 8160 | 9600 | 3840 |  Irr. {3,3,3} |  tr{4,3}×{ } |  tr{4,3}×{ } |  {8}×{6} |  { }×tr{3,3} |  t0,1,2,3{3,3,3} | |
| 51 | 5-demicube hemipenteract (hin) | 26 | 120 | 160 | 80 | 16 |  r{3,3,3} |  h{4,3,3} | - | - | - | - | (16) {3,3,3} | |
| 52 | Cantic 5-cube Truncated hemipenteract (thin) | 42 | 280 | 640 | 560 | 160 |  |  h2{4,3,3} | - | - | - | (16) r{3,3,3} | (16) t{3,3,3} | |
| 53 | Runcic 5-cube Small rhombated hemipenteract (sirhin) | 42 | 360 | 880 | 720 | 160 |  h3{4,3,3} | - | - | - | (16) r{3,3,3} | (16) rr{3,3,3} | ||
| 54 | Steric 5-cube Small prismated hemipenteract (siphin) | 82 | 480 | 720 | 400 | 80 |  h{4,3,3} |  h{4,3}×{} | - | - | (16) {3,3,3} | (16) t0,3{3,3,3} | ||
| 55 | Runcicantic 5-cube Great rhombated hemipenteract (girhin) | 42 | 360 | 1040 | 1200 | 480 |  h2,3{4,3,3} | - | - | - | (16) 2t{3,3,3} | (16) tr{3,3,3} | ||
| 56 | Stericantic 5-cube Prismatotruncated hemipenteract (pithin) | 82 | 720 | 1840 | 1680 | 480 |  h2{4,3,3} |  h2{4,3}×{} | - | - | (16) rr{3,3,3} | (16) t0,1,3{3,3,3} | ||
| 57 | Steriruncic 5-cube Prismatorhombated hemipenteract (pirhin) | 82 | 560 | 1280 | 1120 | 320 |  h3{4,3,3} |  h{4,3}×{} | - | - | (16) t{3,3,3} | (16) t0,1,3{3,3,3} | ||
| 58 | Steriruncicantic 5-cube Great prismated hemipenteract (giphin) | 82 | 720 | 2080 | 2400 | 960 |  h2,3{4,3,3} |  h2{4,3}×{} | - | - | (16) tr{3,3,3} | (16) t0,1,2,3{3,3,3} | ||
| Nonuniform | Alternated runcicantitruncated 5-orthoplex Snub prismatotriacontaditeron (snippit) Snub hemipenteract (snahin) | 1122 | 6240 | 10880 | 6720 | 960 |  sr{3,3,4} | sr{2,3,4} | sr{3,2,4} | - | ht0,1,2,3{3,3,3} | (960) Irr. {3,3,3} | ||
| Nonuniform | Edge-snub 5-orthoplex Pyritosnub penteract (pysnan) | |||||||||||||


 French
French Deutsch
Deutsch