بیضی - ویکی‌پدیا، دانشنامهٔ آزاد

از سلسله مقالاتی دربارهٔ مقاطع مخروطی
سهمی
معادله	${\displaystyle y^{2}=4ax\,}$
گریز از مرکز (${\displaystyle e}$)	${\displaystyle 1\,}$
نیم‌راست‌وتر کانونی (${\displaystyle l}$)	${\displaystyle 2a\,}$
هذلولی
معادله	${\displaystyle {\frac {x^{2}}{a^{2}}}-{\frac {y^{2}}{b^{2}}}=1}$
گریز از مرکز (${\displaystyle e}$)	${\displaystyle {\sqrt {1+{\frac {b^{2}}{a^{2}}}}}}$
نیم‌راست‌وتر کانونی (${\displaystyle l}$)	${\displaystyle {\frac {b^{2}}{a}}}$
بیضی
معادله	${\displaystyle {\frac {x^{2}}{a^{2}}}+{\frac {y^{2}}{b^{2}}}=1}$
گریز از مرکز (${\displaystyle e}$)	${\displaystyle {\sqrt {1-{\frac {b^{2}}{a^{2}}}}}}$
نیم‌راست‌وتر کانونی (${\displaystyle l}$)	${\displaystyle {\frac {b^{2}}{a}}}$
دایره (حالت خاص بیضی)
معادله	${\displaystyle x^{2}+y^{2}=a^{2}\,}$
گریز از مرکز (${\displaystyle e}$)	${\displaystyle 0}$
نیم‌راست‌وتر کانونی (${\displaystyle l}$)	${\displaystyle a}$
• • •
ن ب و

در هندسه، بیضی یک منحنی مسطح و بسته‌است که دو کانون دارد و حاصل جمع فاصلهٔ هر نقطه روی محیط آن با دو کانونش مقدار ثابتی است. شکل بیضی (مقدار کشیده بودنش) با مقدار برون‌مرکزی آن مشخص می‌شود. برون‌مرکزیِ بیضی عددی بین صفر و یک است و هر چه کوچک‌تر باشد کشیدگی بیضی کمتر است. اگر برون‌مرکزی بیضی صفر باشد، دو کانون آن روی هم می‌افتند و منحنی تبدیل به دایره (که حالت خاص بیضی است) می‌شود. بیضی را همچنین می‌توان با عنوان «مقطع مخروطی بسته» تعریف کرد. مقطع مخروطی منحنی‌ای است که در محل تقاطع یک صفحه با یک مخروط پدیدار می‌شود. گونه‌های دیگر مقاطع مخروطی (سهمی و هذلولی) بازند و کراندار نیستند.

قضایا و ویژگی‌های بیضی را نخستین بار ریاضی‌دانان یونان باستان، به ویژه ارشمیدس و آپولونیوس مطالعه کردند. در دوران طلایی اسلام، ریاضی‌دانانی چون اخوان ثلاثهٔ بنوموسی و ابوسهل بیژن کوهی مطالعات نظری و عملی مربوط به بیضی را ادامه دادند. نقاشان رنسانس هم روش‌هایی برای ترسیم بیضی ابداع کردند. در اوایل قرن هفدهم میلادی کپلر کشف کرد که سیارات در مداری بیضوی به دور خورشید می‌گردند و خورشید همواره روی یکی از کانون‌های این بیضی قرار دارد. ریاضی‌دانان فرانسوی، ژرار دوسارگ، بلز پاسکال، رنه دکارت، و فیلیپ دو لا هیر نیز با ترکیب مساعی یونانیان باستان با نمادهای جبری، مقاطع مخروطی را در هندسه تحلیلی مطالعه کردند. قضایای آپولونیوس در باب مماس بر مقاطع مخروطی راهنمای نیوتن و لایبنیتس در ابداع مستقل حساب دیفرانسیل و انتگرال بود. همچنین نیوتن و هالی به روش علمی ثابت کردند که دنباله‌دار هالی در مداری بیضوی به دور خورشید می‌گردد. در قرن نوزدهم میلادی هم ریاضی‌دانانی چون ژان ویکتور پونسله و یاکوب اشتاینر مقاطع مخروطی را با رویکردی تصویری بازتعریف کردند.

ویژگی‌های بیضی در فیزیک، مهندسی و اخترشناسی کاربردهای وسیعی دارد؛ مثلاً مدار هر یک از سیاره‌های منظومه شمسی و قمرهای سیارات به شکل بیضی است، یا اینکه با استفاده از ویژگی «نیمساز عمود زاویهٔ بین دو خط کانونی» می‌توان آینه‌هایی برای تمرکز نور یک منبع در یک کانون ساخت یا طراحی آکوستیک تالارها را بهینه کرد. همچنین از چرخش بیضی به دور قطرهای بزرگ و کوچکش، گوی‌وار کشیده یا پَخ حاصل می‌شود. چنان‌که نیوتن کشف کرد، سیاره‌ها (از جمله زمین) کره نیستند و غالباً شکلی گوی‌وار دارند.

در گذر تاریخ روش‌های متعددی برای ترسیم دقیق یا تقریبی بیضی ابداع شده‌است که از آن میان می‌توان به روش باغبانی، استفاده از خاگار، و تولید مخروطی اشتاینر اشاره کرد. همچنین از آنجا که برای محاسبهٔ محیط بیضی فرمولی با فرم بسته وجود ندارد و باید از حسابان استفاده کرد، فرمول‌های پرشماری برای تخمین این مقدار ارائه شده‌است.

بنابر تقریظی از اراتوستن، نخستین‌بار بیضی را منایخموس (۳۸۰ – ۳۲۰ پ. م)، دوست نزدیک افلاطون، در تلاش برای حل تضعیف مکعب کشف کرد. آپولونیوس برای اولین بار نام «الپسیس» (یونانی:ἔλλειψις، به معنای «کمتر بودن») را بر روی بیضی گذاشت^[۱] و اقلیدس (حدود ۳۶۵–۲۷۵ پ. م) بررسی دقیقی از ویژگی‌های بیضی ارائه کرد.^[۲] کانون‌های بیضی و خط‌های هادی را نخستین بار پاپوس اسکندرانی (حدود ۳۵۰ – ۲۹۰ پ. م) بررسی کرد. او همچنین روشی برای تعریف یک بیضی با داشتن پنج نقطه ابداع کرد.^[۳] ارشمیدس (۲۸۷ – ۲۱۲ پ. م) در گزاره‌های ۷ و ۸ رسالهٔ «در باب مخروط‌گون‌ها و گوی‌گون‌ها»^[الف] طریقهٔ جا دادن یک مخروط را در بیضی مرتبطش بررسی می‌کند. ارشمیدس آگاه بود که با داشتن یک مخروط با مقطع دایره‌ای می‌توان هر بیضی‌ای را ساخت، و می‌دانست که می‌توان بیضی را با برش استوانهای با مقطع دایره‌ای به دست آورد، و اینکه نسبت قطر عرضی بیضی به شعاع دایرهٔ مماس بر آن ثابت است و به مساحت بیضی مربوط می‌شود. در گزاره‌های ۲۷ تا ۳۲ در باب مخروط‌گون‌ها و گوی‌گون‌ها نیز ویژگی‌ها و قضایای مربوط به گوی‌وارها بررسی شده‌است.^[۴]

نام آپولونیوس (اواخر قرن سوم – اوایل قرن دوم پیش از میلاد) برای قرن‌ها پس از مرگ او با مطالعهٔ مقاطع مخروطی گره خورده بود. آپولونیوس اثر مهمش «مخروطات» را، که مشتمل بر هشت مقاله است،^[۵] با مطالعهٔ مخروط آغاز می‌کند و پس از تعریف سه مقطع مخروطی (سهمی، هذلولی، و بیضی)، به تعریف خط مماس آن‌ها می‌پردازد و سپس ثابت می‌کند که فاصلهٔ کانونی برای همهٔ نقاط روی یک بیضی ثابت است.^[۶] آپولونیوس همچنین خط مماس بر منحنی (که بعدها موضوع اصلی حساب دیفرانسیل شد) را تعریف و عدد پی (ثابتی لازم برای یافتن طول‌ها و مساحت دایره و بیضی) را محاسبه کرد.^[۷]

همزمان با حکومت مأمون در خراسان (در قرن سوم هجری)، اخوان ثلاثهٔ بنوموسی دست به ترجمهٔ مخروطات آپولونیوس از یونانی به عربی زدند. بنوموسی فقط نسخه‌ای ناقص از مخروطات را در اختیار داشتند و مقاطع مخروطی در زمان ایشان به دست فراموشی سپرده شده بود، بنابراین در فهم متن دچار مشکل بودند. اندکی بعد، یکی از اخوان ثلاثه به نام حسن نظریهٔ مقاطع استوانه‌ای را ابداع کرد که می‌توان آن را مقدمه‌ای ساده بر مقاطع مخروطی دانست. پس از درگذشت حسن، برادرش احمد در شام نسخه‌ای کامل‌تر از چهار فصل اول مخروطات را با شرح اوتوکیوس پیدا کرد و به کمک برادر دیگرش، محمد، و با استفاده از دو نسخهٔ موجود و نظریهٔ حسن، موفق شد نظریات آپولونیوس را دریابد. احمد و محمد ترجمهٔ مقالهٔ اول تا چهارم مخروطات را به هلال حمصی و مقالهٔ پنجم تا هفتم آن را به ثابت بن قره سپردند و خود بازنگری نهایی ترجمه را عهده‌دار شدند. ترجمهٔ برادران بنوموسی از مقالات پنجم تا هفتم مخروطات تنها نسخهٔ باقی ماندهٔ این اثر است.^[۵] ترجمهٔ آثار علمی به عربی اغلب نیازمند ابداع اصطلاحات فنی تازه بود و مترجمان آن‌ها، برخلاف مترجمان لاتین، به ترانویسی عبارات یونانی اکتفا نکردند^[ب] و برای واژهٔ «الپسیس» اصطلاح «قطع ناقص» را در نظر گرفتند که معنای آن را حفظ می‌کند^[پ] و هنوز در زبان عربی به بیضی «قطع ناقص» گفته می‌شود.^[۵]

کتاب مفقودشدهٔ الشکل المدور المستطیل هم که به حسن بنی موسی منسوب شده‌است در مورد ترسیم بیضی بوده و به نظر می‌رسد بر اساس روش «ترسیم بیضی به روش باغبانی» (رسم بیضی با داشتن مجموع فواصل یک نقطه روی بیضی از دو کانون) باشد. دراین‌صورت ممکن است این اثر اولین جایی باشد که ترسیم بیضی به این روش در آن بحث شده‌است.^[۸] ثابت بن قره نیز (که ترجمهٔ مقالات پنجم تا هفتم مخروطات را برای برادران بنوموسی انجام داده بود) در کتاب في قطوع الاستوانة و بسيطها نگاشتی را مطالعه می‌کند که بیضی با نیم‌قطرهای ${\displaystyle a}$ و ${\displaystyle b}$ را به دایره‌ای با شعاع ${\displaystyle {\sqrt {ba}}}$ انتقال می‌دهد.^[۹]

معماران و بنّاهای دورهٔ اسلامی هم، که به دلایل عملی نیاز به ترسیم بیضی داشته‌اند، ابزاری موسوم به پرگار تام ابداع کردند که با آن می‌توان مقاطع مخروطی را با حرکت اتصالی رسم کرد. ابوسهل بیژن کوهی در قرن چهارم هجری رساله‌ای به نام رسالة في البرکار التام و العمل به دربارهٔ این ابزار نوشته‌است.^[۸]

مشخصات بیضی مدار سیارات

سیاره	نیم‌قطر بزرگ (نسبت به زمین) ${\displaystyle a}$	برون‌مرکزی ${\displaystyle e}$	زاویهٔ صفحهٔ مدار سیاره (نسبت به زمین) ${\displaystyle i}$
عطارد	${\displaystyle 0.387}$	${\displaystyle 0.206}$	${\displaystyle 7^{\circ }00'}$
زهره	${\displaystyle 0.723}$	${\displaystyle 0.007}$	${\displaystyle 5^{\circ }24'}$
زمین	${\displaystyle 1.000}$	${\displaystyle 0.017}$	${\displaystyle 0^{\circ }00'}$
مریخ	${\displaystyle 1.881}$	${\displaystyle 0.093}$	${\displaystyle 1^{\circ }51'}$
مشتری	${\displaystyle 11.857}$	${\displaystyle 0.048}$	${\displaystyle 1^{\circ }18'}$
زحل	${\displaystyle 29.42}$	${\displaystyle 0.056}$	${\displaystyle 2^{\circ }29'}$
اورانوس	${\displaystyle 83.75}$	${\displaystyle 0.046}$	${\displaystyle 7^{\circ }00'}$
نپتون	${\displaystyle 163.72}$	${\displaystyle 0.009}$	${\displaystyle 1^{\circ }46'}$
منبع: University of Denver 2002

علاقه به مطالعهٔ مقاطع مخروطی پس از ارشمیدس و آپولونیوس در اروپای تحت کنترل امپراتوری روم و سپس کلیسای کاتولیک فروکش کرد و تا قرن شانزدهم میلادی پیشرفتی در این مورد روی نداد.^[ت] نخستین نشانهٔ علاقهٔ جدید به مقاطع مخروطی را در لورنزو والا (۱۴۰۷ – ۱۴۶۷ میلادی) می‌توان یافت. کتاب والا، گونه‌ای دائرةالمعارف در مورد علوم مقدماتی است. در فصل سوم از کتاب هشتم بخشی با عنوان «مقاطع مخروطی»^[ث] هست که در آن والا توضیحی کوتاه در مورد مساعی اقلیدس، آپولونیوس، و پاپوس می‌دهد. دو دهه بعد از والا، یوهانس ورنر پژوهش‌هایی در باب مقاطع مخروطی کرد، ولی در آثار او نامی از بیضی نیامده‌است.^[۱۱] به گفتهٔ اروین پانوفسکی،^[ج] طرح اجرانشدهٔ میکل آنژ برای مقبرهٔ پاپ ژولیوس دوم (طراحی شده در ۱۵۰۵ میلادی) به شکل بیضی بوده‌است، ولی اثری از این طرح نمانده. اولین نشانه‌های شکل بیضی در معماری غربی در آثار بالداساره پروتزی (۱۴۸۱ – ۱۵۳۷ میلادی) دیده می‌شود. پس از اینکه سباستیانو سرلیو آثار پروتزی را در کتاب هفت رسالهٔ معماری^[چ] (انتشار در ۱۵۴۷ میلادی) بررسی کرد، استفاده از الگوهای بیضوی در معماری اروپا گسترش یافت.^[۱۲] بااین‌وجود بیضی در میان نقاشان رنسانس، احتمالاً به‌خاطر مطالعات ایشان در باب ژرفانمایی^[ح] شناخته‌شده بود. لئوناردو دا وینچی خود ابزاری برای ترسیم بیضی ساخت و آلبرشت دورر، که از ابزار بیضی‌کِشی دا وینچی باخبر بود، روشی بر اساس تصویرسازی موازی برای ترسیم بیضی ابداع کرد.^[۱۳]

در دههٔ ۱۵۴۰، کوپرنیک نظریه خورشیدمرکزیاش را ارائه کرد. در مدل خورشیدمرکزی کوپرنیک مسیر حرکت سیارات به دور خورشید به شکل دایره است؛ این امر با داده‌های ریاضی موجود نمی‌خوانْد و کوپرنیک خود از این نارسایی مدلش آگاه بود.^[۱۴] در ۱۶۰۲ میلادی، کپلر در پی رفع نارسایی‌هایی مدل کوپرنیک به این نتیجه رسید که مسیر حرکت سیارات به شکل تخم‌مرغ (خایوی) است^[۱۵] و فواصل بین آنها بر اساس اجسام افلاطونی تعیین می‌شود. تیکو براهه (۱۵۴۶–۱۶۰۱ م) با تکیه بر مشاهداتش از حرکت مریخ، نظریات کپلر را دربارهٔ شکل منظومهٔ شمسی رد کرد و کپلر را دعوت کرد که به رصدخانهٔ او در پایتخت امپراتوری مقدس روم پراگ برود. کپلر، در تلاش برای حل ناهماهنگی بین مدلش از هستی و مشاهدات براهه، به این کشف مهم نایل شد که سیارات در مداری بیضوی و نه مدور به دور خورشید می‌گردند.^[۱۶] بنابر قانون اول کپلر، خورشید همواره روی یکی از کانون‌های این بیضی قرار دارد.^[۱۷] عبارت «کانون بیضی» را هم (که مفهوم آن را سده‌ها پیش آپولونیوس بیان کرده بود) کپلر نخستین بار در سال ۱۶۰۹ در کتاب ستاره‌شناسی نوین به کار برد.^[۱۸] به نوشتهٔ کپلر در این کتاب، خورشید موتوری است که نیروی لازم برای حرکت سیاره‌ها را فراهم می‌کند و سرعت سیاره‌ها با نزدیک شدن به خورشید در خم مدارشان بیشتر می‌شود.^[۱۹]

در سال ۱۵۷۸ میلادی، اسقف کلیسای انطاکیه آثاری شرقی را به فردیناندو دو مدیچی تقدیم کرد که در میان آن‌ها نسخه‌ای از مخروطات با ویرایش و اضافات ابوالفتح اصفهانی بود. مسئول کتابخانهٔ فردیناندو، جیووانی باتیستا^[خ] از اهمیت مخروطات آگاه بود و بر آن بود که ترجمه‌ای از آن را منتشر کند، ولی پیش از انجام این کار درگذشت. گالیلئو گالیله نیز در چندین نامه خبر از قصدش برای ترجمهٔ مخروطات به لاتین داده بود اما به‌نظر تلاش چندانی در این زمینه انجام نداده‌است. در نهایت در سال ۱۶۶۱ ریاضی‌دان ایتالیایی جووانی آلفونسو بورلیِ با کمک کشیش مارونی ابراهیم حاقلانی موفق به ترجمه و چاپ مخروطات به لاتین شد. از آنجا که ابوالفتح اصفهانی در ترجمه‌اش قضایای مختلف را با هم ترکیب کرده بود و وفاداری چندانی به نسخهٔ اصلی آپولونیوس نداشت، ترجمهٔ لاتین بورلی تفاوت‌های متعددی با نسخهٔ اصلی مخروطات دارد.^[۲۰]

همزمان دو نسخهٔ عربی دیگر از مخروطات به اروپا رسید. یکی نسخه‌ای نفیس از مخروطات بنوموسی (که امروزه در گنجینهٔ کتابخانه بادلین دانشگاه آکسفورد نگهداری می‌شود) و دیگری نسخه‌ای با ویرایش و اضافات عبدالملک شیرازی. ژاکوب گولیوس توانست هر دو نسخه را قرض بگیرد و نسخه‌ای کپی از روی آن‌ها بنویسد. گولیوس سپس، احتمالاً با کمک رنه دکارت، دست به ترجمهٔ مخروطات زد، ولی آن را چاپ نکرد و این اثر تا سی سال پس از مرگش در ۱۶۶۷ چاپ نشد. در نهایت ورثهٔ گولیوس در ۱۶۹۶ آثار او از جمله ترجمهٔ مخروطات را فروختند.^[۲۱]

ریاضی‌دانان فرانسوی ژرار دوسارگ و بلز پاسکال مطالعهٔ مقاطع مخروطی را به فراتر از دانسته‌های یونانیان باستان گسترش دادند. ریاضی‌دان هم‌وطن آنان کلود میدورژ نیز اثبات‌های آپولونیوس را به شیوه‌ای سیستماتیک مدون کرد. در سال ۱۶۴۷ (کمتر از یک دهه پس از انتشار اثر میدورژ)، گرگوآر د سن-ویسنت نیز کتاب خود را با عنوان «اثر چهاربخشی هندسی: دایره و مقاطع مخروط»^[د] منتشر کرد. در این کتاب هر مقطع مخروطی بخش مخصوص خودش را دارد و تعدادی قضیه دربارهٔ هر یک اثبات شده‌است. بخش مربوط به بیضی مشتمل بر ۲۰۴ قضیه است. سن-وینسنت بیضی را به شیوهٔ ارشمیدس^[ذ] تعریف می‌کند.

یوهان د ویت هلندی (۱۶۲۵–۱۶۷۲ میلادی) هم بخش اول رساله‌ای که در ۱۶۵۸ چاپ کرد را به مقاطع مخروطی اختصاص داده‌است و بیضی را با روشی بدیع به عنوان مکان هندسی نقاطی با فاصلهٔ ثابت از یک خط و یک نقطه تعریف می‌کند. د ویت که تحت تأثیر دکارت بود تلاش داشت یافته‌های هندسی یونانیان را با نمادهای جبری بیان کند. بااین‌حال نقش اصلی در توسعهٔ هندسهٔ دکارتی بر عهدهٔ شاگرد دوسارگ فیلیپ دو لا هیر بود. لا هیر، در اثری که به خزانه‌دار فرانسه ژان-باتیست کولبر تقدیم شده‌است، اصول هندسی را به زبان ساده و آسان توضیح می‌دهد. هر مقطع مخروطی در فصل مخصوص خود بررسی شده‌است. بیضی به عنوان مکان هندسی نقاطی با مجموع ثابت فواصل از دو نقطه تعریف می‌شود و ویژگی‌های خط مماس، قطرهای مزدوج، و معادلهٔ آن بیان شده‌است و پس از آن بحثی در مورد مختصات دکارتی مقاطع مخروطی آمده‌است.^[۲۲] رنه دکارت خود مقاطع مخروطی آپولونیوس، به‌ویژه بیضی و سهمی، را در آثارش در باب هندسه تحلیلی بررسی کرده بود.^[۲۳] بااین‌حال مهم‌ترین اثر لا هیر «مقاطع مخروطی»^[ر] نام دارد و از نُه کتاب تشکیل شده‌است. لا هیر در کتاب ۲ مخروط را به شیوهٔ آپولونیوس بیان می‌دارد و تعریف‌های جدیدی (از جمله directrix یا «خط هادی»، به عنوان خطی که با تبدیل بیضی به دایره به سمت بینهایت میل می‌کند) را نیز ارائه می‌کند. در کتاب ۳ معادلهٔ مقاطع مخروطی حاصل می‌شود و بقیهٔ اثر هم کم‌وبیش به شرح آرای آپولونیوس می‌پردازد.^[۲۴]

نیوتن (۱۶۴۲–۱۷۲۷) در اصول ریاضی فلسفه طبیعی علاقهٔ خاصی به مقاطع مخروطی نشان می‌دهد و آن‌ها را «مسیر»^[ز] می‌نامد.^[۲۵] نیوتن با روشی که امروزه به «ساخت طبیعی نیوتن» موسوم است «مسیر» ها را با داشتن پنج نقطه تعریف می‌کند. سپس با استفاده از نگاشت خطی هر مسیر را با داشتن چهار نقطه و یک خط مماس، سه نقطه و دو خط مماس، و یک نقطه و چهار خط مماس تعریف می‌کند.^[۲۶] مساعی آپولونیوس در باب مقاطع مخروطی، به‌ویژه مبحث خط مماس بر منحنی، راهنمای هر دوی نیوتن و لایبنیتس در ابداع مستقل حساب دیفرانسیل و انتگرال (انتشار در ۱۶۸۴ میلادی) بود.^[۲۷] همچنین نیوتن با استفاده از حساب دیفرانسیل و انتگرال و قوانین نیوتن مدار حرکت سیاره‌ها در بیضی کپلر را ثابت کرد.^[۲۸]

بین سال‌های ۱۶۸۲ و ۱۷۰۵، ادموند هالی به منظور اثبات قوانین کپلر و قوانین نیوتن^[ژ] مشاهدات دقیقی را از حرکت دنباله‌داری که امروزه با نام او شناخته می‌شود انجام داد. نیوتن و هالی ثابت کردند که این دنباله‌دار در مداری بیضوی به دور خورشید می‌گردد و پیش‌بینی کردند که در ۱۷۵۸ در آسمان نمایان خواهد شد.^[۳۰][۳۱] نیوتن همچنین در اصول ریاضی فلسفه طبیعی بیش‌بینی کرد که شکل کرهٔ زمین کروی نیست و به شکل گوی‌وار پَخ (حجمی که از چرخش بیضی به دور قطر کوچکش حاصل می‌شود) است. در ۱۷۳۶، دانشمند فرانسوی پی‌یر لوئی موپرتوئی به پشتیبانی لوئی پانزدهم سفری تجسسی به لاپ‌لند انجام داد و این نظریهٔ نیوتن را ثابت کرد.^[س][۳۳] هالی همچنین تلاش داشت با مقابلهٔ نسخه‌های بنوموسی، اصفهانی، و شیرازی مخروطات آپولونیوس را دقیقاً «بازسازی» کند و به همین منظور زبان عربی را آموخت. در سال ۱۷۱۰ نسخهٔ هالی از مخروطات با عنوان مقاطع مخروطی آپولونیوس پرگا از نسخ عربی^[ش] به چاپ رسید. تا زمان ترجمهٔ توماس هیت از مخروطات در سال ۱۸۹۶، ترجمهٔ هالی نسخهٔ استاندارد و آموزشی این اثر باقی ماند.^[۳۴]

در دو قرن پس از نیوتن، عمدهٔ پیشرفت‌های مرتبط با مقاطع مخروطی در زمینهٔ هندسه تصویری صورت گرفت. ژان ویکتور پونسله در سال ۱۸۱۳ در جریان جنگ‌های ناپلئونی در روسیه اسیر جنگی بود و در زندان رساله‌ای با عنوان «خواص و ویژگی‌های تصاویر اشکال»^[ص] نوشت و در آن برای اولین بار بین ویژگی‌های تصویری (ویژگی‌هایی که پس از تصویر کردن شکل در صفحه‌ای دیگر حفظ می‌شوند) و غیرتصویری تمایز قائل شد.^[۳۵] در ۱۸۲۲ ریاضی‌دان بلژیکی جرمینال پیر دندلین با ابداع کره‌های دندلین اثبات کرد که بیضی ساخته‌شده با استفاده از تعریف کانونی و بیضی ساخته‌شده با برخورد صفحه و مخروط یکی‌اند.^[۳۶] در ۱۸۲۹ نیز پیرس مورتون^[ض] با استفاده از کره‌های دندلین ثابت کرد که بیضی ساخته‌شده با تعریف کانون و خط هادی هم با بیضی ساخته شده در تقاطع صفحه و مخروط یکی است. یاکوب اشتاینر (۱۷۹۶–۱۸۶۳) نیز مقاطع مخروطی و رویه‌های درجه دوم مرتبط را به‌عنوان اشکالی صرفاً تصویری تعریف کرد و نشان داد که این برخورد به اثبات سریع‌تر و مستقیم‌تر ویژگی‌های آن‌ها می‌انجامد.^[۳۷] کارل گئورگ کریستیان فان اشتات (۱۷۹۸–۱۸۶۷) هم نشان داد که رابطه‌ای که یک مقطع مخروطی بین قطب و خط قطبی ایجاد می‌کند از خود منحنی بنیادی‌تر است و می‌تواند برای تعریف این منحنی‌ها به شکلی متقارن و برگشتی (به عنوان مکان هندسی نقاطی که روی خط قطبی خودشانند، یا منحنی محاطی خطوطی که از قطب خودشان می‌گذرند) به‌کار رود.^[۳۸]

با استفاده از ویژگی «نیمساز عمود زاویه بین دو خط کانونی» می‌توان نورپردازی و طراحی آکوستیک ساختمان‌ها را بهینه کرد.^[۳۹] منطقه فرنل نیز با همین ویژگی بیضی به شکل گوی‌وار ایجاد می‌شود و درک آن برای طراحی شبکه‌های بی‌سیم ضروری است. از آینههای بیضوی نیز برای تمرکز نور یک منبع در کانونی معین استفاده می‌شود. مدار بیضی در اخترپویاشناسی مداری کپلری است که برون‌مرکزی آن کمتر از ۱ باشد. نمونه‌های مدار بیضی، از جمله مدار هوهمان، در محاسبات پیش‌رانش فضاپیماها و مدار ماهوارهها اهمیت زیادی دارد. جواب عام نوسانگر هماهنگ در دو بعد یا بیشتر هم بیضی است. می‌توان چرخ‌دنده‌هایی به شکل بیضی ساخت که هر یک به محور یکی از کانون‌هایشان به‌نرمی مماس یکدیگر بچرخند.^[۴۰] چرخ‌دنده‌های بیضوی معمولاً زمانی به‌کار می‌روند که سرعت متغیر حرکت چرخ‌دنده مطلوب باشد. در سیاست بین‌الملل، عبارت بیضی استراتژیک اشاره به منطقه‌ای در غرب آسیا دارد که دربرگیرندهٔ بیش از ۷۰ درصد ذخایر اثبات‌شدهٔ نفت و بیش از ۶۵ درصد ذخایر اثبات‌شدهٔ گاز طبیعی جهان است. نقشهٔ دفتر اصلی رئیس‌جمهور آمریکا در کاخ سفید به شکل بیضی است. به نوشتهٔ کریسچن ساینس مانیتور، وجود دو کانون در دفتر بیضی نماد دو کانون وظیفه در تصمیم‌گیری‌های سیاسی (سیاستمداران و مردم) است.^[۴۱]

بیضی را می‌توان به عنوان نتیجهٔ اعمال یک نگاشت خطی (تبدیل آفین) بر دایرهای به شعاع یک تعریف کرد. اگر ${\displaystyle a}$ و ${\displaystyle b}$ اعدادی بزرگتر از صفر باشند، ماتریس این نگاشت عبارت است از:^[۴۲]

اگر ${\displaystyle a}$ کمتر از ۱ باشد، بیضی حاصل از این نگاشت دایره در راستای محور xها فشرده می‌شود و اگر ${\displaystyle a}$ بیشتر از ۱ باشد بیضی در این راستا کشیده می‌شود. همین‌طور اگر ${\displaystyle b}$ کمتر از ۱ باشد، بیضی حاصل از این نگاشت دایره در راستای محور yها فشرده می‌شود و اگر ${\displaystyle b}$ بیشتر از ۱ باشد بیضی در این راستا کشیده می‌شود. قطر بزرگ بیضی دو برابر هر کدام از ${\displaystyle a}$ یا ${\displaystyle b}$ است که بزرگتر باشد و قطر کوچک بیضی دو برابر آنی که کوچکتر باشد. مساحت بیضی هم برابر است با ${\displaystyle A=\pi ab}$.^[۴۳]

از سوی دیگر، با اعمال تجانس ${\displaystyle (x,y)\rightarrow (x_{1},y_{1})=(x,y\cdot a/b)}$ هم، که در آن رأس‌های بزرگ ثابت می‌مانند و رأس‌های کوچک به ${\displaystyle (0,a)}$ و ${\displaystyle (0,-a)}$ منتقل می‌شوند، می‌توان بیضی را به دایرهای با شعاع ${\displaystyle a}$ تبدیل کرد.^[۴۴]

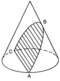
بیضی خمی بسته‌است که از برخورد مخروطی قائم با قاعدهٔ دایره‌ای و صفحه‌ای حاصل می‌شود که با ارتفاع و هر کدام از وترهای مخروط موازی نباشد.^[۴۵] اگر این صفحه با قاعدهٔ مخروط موازی باشد حاصل دایره (حالت خاص بیضی)، اگر با ارتفاع مخروط موازی باشد حاصل هذلولی، و اگر با یکی از وترهای مخروط موازی باشد حاصل سهمی خواهد بود.^[۴۶]

در هندسه تصویری، اشتقاق بیضی از مخروط معادل تصویر مرکزی یک دایره (مقطع مخروط) روی صفحه‌ای است که با صفحهٔ دایره زاویه‌ای تند دارد. می‌توان نشان داد که تصویر کردن دایره روی بیضی همان تعریف بیضی با اعمال تجانس آفین بر دایره است.^[۴۷]

تعریف دیگری از بیضی این است که بیضی مکان هندسی همهٔ نقاطی است که مجموع فاصله‌هایشان از دو نقطهٔ ثابت (دو کانون) ثابت و برابر قطر بزرگ بیضی است. هر چه فاصلهٔ بین این دو نقطه کمتر باشد، خروج از مرکز بیضی کوچکتر است و شکل بیضی به دایره شبیه‌تر.^[۴۸]

قطر بزرگ بیضی خط راستی است که دو کانون آن را به هم متصل می‌کند و از دو طرف تا منحنی ادامه می‌یابد. قطر کوچک بیضی عمود بر نقطهٔ وسط قطر بزرگ (با فاصلهٔ یکسان از دو کانون) قرار دارد. به دو خطی که به موازات قطر کوچک بیضی رسم می‌شوند و از کانون‌ها می‌گذرند «راست‌وتر کانونی»^[ط] گفته می‌شود.^[۴۹]

اثبات

با استفاده از کره‌های دندلین می‌توان اثبات کرد که بیضی تعریف‌شده با دو کانون با بیضی ساخته‌شده از برخورد مخروط و صفحه یکی است.^[۵۰] گیریم صفحهٔ ${\displaystyle e}$ مخروطی را قطع می‌کند و در محل انقطاع یک منحنی تشکیل شده‌است. دو کرهٔ دندلین ${\displaystyle G_{1}}$ روی صفحه و ${\displaystyle G_{2}}$ زیر صفحه تعریف شده‌اند. تقاطع هر کره با مخروط یک دایره است (${\displaystyle k_{1}}$ و ${\displaystyle k_{2}}$)، و هر کره بر صفحهٔ ${\displaystyle e}$ را در یک نقطه (${\displaystyle F_{1}}$ و ${\displaystyle F_{2}}$) مماس است. گیریم P نقطه‌ای روی منحنی باشد. قصد است که ثابت شود با حرکت ${\displaystyle P}$ بر روی منحنی، فاصلهٔ ${\displaystyle d(F_{1},P)+d(F_{2},P)}$ ثابت می‌ماند:

• گیریم خطی که از ${\displaystyle P}$ و رأس ${\displaystyle S}$ می‌گذرد دو دایره را در نقاط ${\displaystyle P_{1}}$ و ${\displaystyle P_{2}}$ قطع کند.
• با حرکت ${\displaystyle P}$ بر روی منحنی، ${\displaystyle P_{1}}$ و ${\displaystyle P_{2}}$ بر روی دو دایره حرکت می‌کنند.
• ${\displaystyle PF_{1}}$ و ${\displaystyle PP_{1}}$ هر دو از نقطهٔ ${\displaystyle P}$ آغاز شده‌اند و بر دایرهٔ ${\displaystyle G_{1}}$ مماسند، پس ${\displaystyle PF_{1}=PP_{1}}$ (چرا که دو مثلث قائم‌الزاویهٔ ${\displaystyle MPF_{1}}$ و ${\displaystyle MPP_{1}}$ همنهشتند).
• به همین ترتیب ${\displaystyle PF_{2}=PP_{2}}$.
• از آنجا که ${\displaystyle k_{1}}$ و ${\displaystyle k_{2}}$ موازی‌اند، فاصلهٔ ${\displaystyle P_{1}}$ و ${\displaystyle P_{2}}$ همواره عدد ثابتی است؛ بنابراین با حرکت ${\displaystyle P}$ روی منحنی فاصلهٔ ${\displaystyle d(F1,P)+d(F2,P)}$ ثابت می‌ماند. پس ثابت می‌شود که منحنی مورد بحث همان بیضی است.^[۵۱]

بیضی را می‌توان با مسیر نقطه‌ای تعریف کرد که به‌گونه‌ای در صفحه حرکت می‌کند که نسبت فاصله‌اش از یک نقطهٔ خاص (کانون) و فاصله‌اش از خطی صاف (خط هادی) عددی ثابت و کوچکتر از یک باشد. هر مسیری که این شرط را احراز کند همین ویژگی را نسبت به یک کانون و خط هادی دیگر هم دارد، ازین‌رو بیضی را می‌توان با داشتن یکی از کانون‌ها و خط هادی متناظرش تعریف کرد. نسبت این فواصل با خروج از مرکز و مقدار مبین^[ظ] در معادلهٔ کلی همهٔ مقاطع مخروطی برابر است.^[۵۲]

اثبات

اگر کانون برابر ${\displaystyle F=(f_{1},f_{2})}$ و معادلهٔ خط هادی ${\displaystyle ux+vy+w=0}$ باشد، نتیجه می‌شود:

${\displaystyle \left(x-f_{1}\right)^{2}+\left(y-f_{2}\right)^{2}=e^{2}\cdot {\frac {\left(ux+vy+w\right)^{2}}{u^{2}+v^{2}}}\ .}$

(در سمت راست معادله فاصلهٔ ${\displaystyle |Pl|}$ با صورت نرمال هسه محاسبه می‌شود)^[۵۳]

با استفاده از کره‌های دندلین هم می‌توان اثبات کرد که بیضی حاصل از تعریف با کانون و خط هادی همان بیضی حاصل شده از تقاطع یک صفحه و یک مخروط است.

معادلهٔ بیضی را می‌توان بر اساس معادلهٔ دایره و با اعمال نگاشت خطی ${\displaystyle M={\begin{bmatrix}a&&0\\0&&b\end{bmatrix}}}$ بر آن به دست آورد. گیریم ${\displaystyle (x_{1},y_{1})}$ نقطه‌ای بر روی دایره‌ای باشد که بر روی نقطهٔ ${\displaystyle (x,y)}$ بیضی نگاشت شده‌است:

${\displaystyle M({\frac {x_{1}}{y_{1}}})=({\frac {x}{y}})}$

از آنجا که دترمینان ${\displaystyle M}$ صفر نیست، ${\displaystyle M}$ وارون‌پذیر است. ماتریس وارون ${\displaystyle M}$ را می‌توان با قاعده کرامر به‌دست‌آورد:^[۵۴]

${\displaystyle M^{-1}={\frac {1}{ab}}{\begin{bmatrix}a&&0\\0&&b\end{bmatrix}}={\begin{bmatrix}{\frac {1}{b}}&&0\\0&&{\frac {1}{a}}\end{bmatrix}}}$

با اعمال ${\displaystyle M^{-1}}$ بر نقاط ${\displaystyle (x,y)}$ بیضی، نقاط ${\displaystyle (x_{1},y_{1})}$ دایره حاصل می‌شود:

${\displaystyle M^{-1}{\begin{bmatrix}x\\y\end{bmatrix}}={\begin{bmatrix}{\frac {x}{a}}\\{\frac {y}{b}}\end{bmatrix}}={\begin{bmatrix}x_{1}\\y_{1}\end{bmatrix}}}$

و با قرار دادن ${\displaystyle (x_{1},y_{1})=({\frac {x}{a}},{\frac {y}{b}})}$ در معادله دایره (${\displaystyle x_{1}^{2}+y_{1}^{2}=1}$)، معادلهٔ بیضی حاصل می‌شود:^[۵۵]

${\displaystyle ({\frac {x}{a}})^{2}+({\frac {y}{b}})^{2}=1}$

هر معادله درجه دو با فرمول ${\displaystyle a^{2}\cdot x^{2}+b^{2}\cdot y^{2}-a^{2}\cdot b^{2}=0}$ معرف یک بیضی است که مرکزش روی مبدأ مختصاتی، قطر بزرگش روی محور ${\displaystyle x}$ها، و قطر کوچکش روی محور ${\displaystyle y}$ها جای دارد. مقادیر ${\displaystyle a}$ و ${\displaystyle b}$ فاصلهٔ چهار رأس بیضی را از مرکز آن مشخص می‌کنند، به گونه‌ای که مختصات رأس‌های بزرگ ${\displaystyle (a,0)}$ و ${\displaystyle (-a,0)}$ و مختصات راس‌های کوچک ${\displaystyle (0,b)}$ و ${\displaystyle (0,-b)}$ است.^[۵۶] مقدار ${\displaystyle b}$ به «نیم‌قطر کوچک»^[ع] و مقدار ${\displaystyle a}$ به «نیم‌قطر بزرگ»^[غ] موسوم است.^[۵۷] این معادله غالباً به شکل ${\displaystyle {\frac {x^{2}}{a^{2}}}+{\frac {y^{2}}{b^{2}}}=1}$ نوشته می‌شود. فاصلهٔ مرکز بیضی از هر کدام از کانون‌ها ${\displaystyle c={\sqrt {(b^{2}-a^{2})}}}$ و مختصات کانونها ${\displaystyle (\pm c,0)}$ است.

اگر مرکز بیضی از مبدأ مختصاتی به نقطهٔ ${\displaystyle (x_{0},y_{0})}$ انتقال یابد معادلهٔ بیضی برابر ${\displaystyle {\frac {(x-x_{0})^{2}}{a^{2}}}+{\frac {(y-y_{0})^{2}}{b^{2}}}=1}$ خواهد بود.^[۵۸]

برای اینکه معادلهٔ عام منحنی‌های درجه دو (یعنی

${\displaystyle ax^{2}+2bxy+cy^{2}+2dx+2fy+g=0}$

) بیضی باشد، باید تعریف کرد که

${\displaystyle {\begin{aligned}\Delta ={\begin{bmatrix}a&b&d\\b&c&f\\d&f&g\end{bmatrix}},\\J={\begin{bmatrix}a&b\\b&c\end{bmatrix}},\\I=a+c\end{aligned}}}$

که در آن ${\displaystyle J>0}$، ${\displaystyle \Delta \neq 0}$، و ${\displaystyle {\tfrac {\Delta }{I}}<0}$ است. در این معادله اگر ${\displaystyle a=c}$ باشد حاصل دایره خواهد بود (که حالت خاصی از بیضی است) و اگر ${\displaystyle \Delta =0}$ حاصل یک نقطه می‌شود. مختصات مرکز این بیضی ${\displaystyle (x_{0},y_{0})}$ از معادلات زیر حاصل می‌شود:^[۵۹]

${\displaystyle x_{0}={\frac {cd-bf}{b^{2}-ac}},}$

${\displaystyle y_{0}={\frac {af-bd}{b^{2}-ac}}.}$

و محورهای نیم‌بزرگ و نیم‌کوچک بیضی عبارت است از:^[۶۰]

${\displaystyle a'={\sqrt {\frac {2(af^{2}+cd^{2}+gb^{2}-2bdf-acg)}{(b^{2}-ac){\big [}{\sqrt {(a-c)^{2}+4b^{2}}}-(a+c){\big ]}}}}}$

${\displaystyle b'={\sqrt {\frac {2(af^{2}+cd^{2}+gb^{2}-2bdf-acg)}{(b^{2}-ac){\big [}-{\sqrt {(a-c)^{2}+4b^{2}}}-(a+c){\big ]}}}}}$

معادلهٔ پارامتری بیضی را می‌توان با اعمال تجانس (تبدیل آفین) ${\displaystyle y_{1}=b\cdot y}$، ${\displaystyle x_{1}=a\cdot x}$ بر معادلهٔ پارامتری دایره واحد (یعنی ${\displaystyle c_{1}(t)=(cos(t),sin(t))}$) به‌دست‌آورد. با این حساب معادلهٔ پارامتری بیضی عبارت است از:

${\displaystyle d_{1}(t)=(a\cdot cos(t),b\cdot sin(t))}$

که در آن ${\displaystyle 0\leq t<2\pi }$.^[۶۱]

برای یافتن معادلهٔ پارامتری بیضی به صورت عبارت‌های گویا، می‌توان همان تجانس ${\displaystyle y_{1}=b\cdot y}$، ${\displaystyle x_{1}=a\cdot x}$ را بر معادلهٔ پارامتری گویای دایره‌ای به شعاع واحد اعمال کرد. در این حالت معادلهٔ پارامتری بیضی عبارت است از:^[۶۲]

${\displaystyle d_{1}(t)=(a\cdot {\frac {2t}{1+t^{2}}},b\cdot {\frac {1-t^{2}}{1+t^{2}}})}$

معادلهٔ قطبی بیضی معمولاً به مرکزیت یکی از کانون‌های آن نوشته می‌شود. اگر آغاز زاویهٔ ${\displaystyle \theta }$ از قطر بزرگ یک بیضی باشد، معادلهٔ قطبی آن عبارت است از:

${\displaystyle r(\theta )={\frac {a(1-e^{2})}{1+e\cos \theta }}}$

زاویهٔ ${\displaystyle \theta }$ به آنومالی حقیقی کانون مورد نظر موسوم است و گاه با ${\displaystyle w}$ هم نشان داده می‌شود. ثابت ${\displaystyle a(1-e^{2})}$ هم همان «نیم‌راست‌وتر کانونی» (${\displaystyle p}$) است. نقطهٔ ${\displaystyle A}$ که در آن مقدار ${\displaystyle r}$ به حداقل خود می‌رسد «نقطهٔ حضیض»^[ف] و نقطهٔ ${\displaystyle B}$ که در آن مقدار ${\displaystyle r}$ به حداکثر خود می‌رسد «نقطهٔ اوج»^[ق] نام دارد.^[۶۳]

مختصات دوقطبی بیضی‌ای که یکی از کانون‌هایش روی مبدأ مختصات باشد عبارت است از معادلهٔ

${\displaystyle r_{1}+r_{2}=2a}$

که در آن ${\displaystyle a}$ برابر نصف قطر بزرگ بیضی است.^[۶۴]

هر بیضی روی قطر بزرگش دو کانون دارد که با نمادهای ${\displaystyle f_{1}(e,0)}$ و ${\displaystyle f_{2}(-e,0)}$ نشان داده می‌شود. مقدار ${\displaystyle e}$ (خروج از مرکز^[ک]) را می‌توان با جایگزین کردن ${\displaystyle a}$ و ${\displaystyle b}$ در فرمول ${\displaystyle c^{2}=a^{2}-b^{2}}$ ,

محاسبه کرد. با دانستن این فرمول و استفاده از قضیه فیثاغورث، مشخص است که فاصلهٔ رأس‌های کوچک تا ${\displaystyle f_{1}}$ و ${\displaystyle f_{2}}$ برابر ${\displaystyle a}$ است. این امر حالت خاصی از ویژگی زیر است:

مجموع فواصل هر نقطهٔ ${\displaystyle p}$ روی محیط بیضی از دو کانون (${\displaystyle dist(p,f_{1})+dist(p,f_{2})}$) برای هر بیضی همواره ثابت است.^[۶۵]

بنابراین هر بیضی را می‌توان با داشتن دو کانون و یک نقطه روی محیط ترسیم کرد. برای اثبات این ویژگی، می‌توان نقطهٔ ${\displaystyle p(x,y)}$ را تعریف و در فرمول فاصله جایگزین کرد:

${\displaystyle dist(p,f_{1})+dist(p,f_{2})={\sqrt {(x-e)^{2}+y^{2}}}+{\sqrt {(x+e)^{2}+y^{2}}}}$

و با استفاده از معادلهٔ بیضی (${\displaystyle b^{2}\cdot x^{2}+a^{2}\cdot x^{2}-a^{2}\cdot b^{2}=0}$) می‌توان نشان داد که این مقدار برابر ${\displaystyle 2a}$ است.^[۶۶]

نسبت فاصلهٔ هر کانون از مرکز بیضی (${\displaystyle c}$) به اندازه نیم‌قطر بزرگ بیضی (${\displaystyle a}$) برون‌مرکزی بیضی نامیده می‌شود و آن را با حرف ${\displaystyle e}$ نشان می‌دهند (${\displaystyle e={\tfrac {c}{a}}}$). به‌این‌ترتیب برون‌مرکزی را می‌توان جای کانون در نیم‌قطر بزرگ دانست. برون‌مرکزی یک بیضیِ معین همواره مقداری ثابت و بین صفر و یک است ${\displaystyle (0\leq e<1)}$ و به‌صورتی یکتا شکل آن را مشخص می‌کند، به این مفهوم که دو بیضی متشابهند اگر و تنها اگر برون‌مرکزی‌شان با هم برابر باشد. زمانی که برون‌مرکزی صفر باشد، کانون روی مرکز می‌افتد و منحنی به‌شکل دایره درمی‌آید. اگر برون‌مرکزی به یک نزدیک شود (فاصلهٔ کانون از مرکز به بی‌نهایت میل کند)، بیضی حالتی کشیده پیدا می‌کند.^[۶۷]

برون‌مرکزی بیضی برابر وارون ضربی برون مرکزی هذلولیای با نیم‌قطر بزرگ و کوچک برابر است.^[۶۸]

اگر ${\displaystyle a}$ نیم‌قطر بزرگ بیضی و ${\displaystyle c}$ فاصلهٔ هر کانون بیضی از مرکز آن باشد، دو خط موازی با قطر کوچک بیضی به فاصلهٔ ${\displaystyle d={a^{2}}{c}}$ از این قطر به خطوط هادی بیضی موسومند. می‌توان نشان داد که در هر بیضی نسبت «فاصلهٔ نقطهٔ ${\displaystyle p}$ از هر کدام از کانون‌های بیضی» به «فاصلهٔ ${\displaystyle p}$ از خط هادی متناظر با آن کانون» ثابت و برابر با برون‌مرکزی بیضی است؛ یعنی:^[۶۹]

اگر نسبت فاصله هر نقطه روی بیضی از کانون به فاصله‌اش از خط هادی برابر ${\displaystyle r}$، فاصلهٔ خط هادی از مرکز بیضی برابر ${\displaystyle d}$، و نیم‌قطر کوچک بیضی ${\displaystyle b}$ باشد آنگاه:

${\displaystyle r={\frac {a-c}{d-a}}={\frac {\sqrt {b^{2}+c^{2}}}{d}}}$

و برای به دست آوردن ${\displaystyle d}$:

${\displaystyle d={\frac {\sqrt {b^{2}+c^{2}}}{r}}}$

به موازات هر وتر ${\displaystyle AB}$ که از مرکز بیضی بگذرد، مجموعه‌ای از وترها هست که شامل خط مماس بر بیضی با شیب مساوی ${\displaystyle AB}$ می‌شود. با وصل کردن نقطهٔ وسط همهٔ این وترها به هم ${\displaystyle CD}$ حاصل می‌شود که قطر بیضی است و با عنوان «مزدوج»^[گ] ${\displaystyle AB}$ شناخته می‌شود. با استفاده از قطرهای مزدوج بر وتر می‌توان خطوط مماس بر بیضی را ترسیم کرد. خطوط مماس بر نقاط${\displaystyle A}$، ${\displaystyle B}$، ${\displaystyle C}$، و ${\displaystyle D}$ بیضی را در یک متوازی‌الأضلاع محاط می‌کنند. اگر وتر ${\displaystyle AB}$ همنهشت بر یکی از قطرهای بیضی شود، شکل محاط‌کنندهٔ بیضی مستطیل خواهد بود.^[۷۰]

وتری که از یکی از کانون‌ها می‌گذرد و بر قطر بزرگ بیضی عمود است «راست‌وتر کانونی» نامیده می‌شود. نصف این وتر، یعنی «نیم‌راست‌وتر کانونی»^[ل] است که با حرف ${\displaystyle p}$ نمایش داده می‌شود. می‌توان نشان داد که:

${\displaystyle p={\frac {b^{2}}{a}}}$

همچنین می‌توان با استفاده از معادلهٔ قطبی بیضی نشان داد که:^[۷۱]

${\displaystyle p=a(1-e^{2})}$

اگر خطی یک بیضی را در ۱ و فقط ۱ نقطه قطع کند، گفته می‌شود که آن خط بر آن بیضی مماس است. از هر نقطه روی بیضی تنها یک خط مماس می‌گذرد. معادلهٔ خط مماس بیضی ${\displaystyle \;{\tfrac {x^{2}}{a^{2}}}+{\tfrac {y^{2}}{b^{2}}}=1\;}$ در نقطهٔ ${\displaystyle (x_{0},y_{0})}$ عبارت است از:

${\displaystyle \ {\frac {x_{0}}{a^{2}}}x+{\frac {y_{0}}{b^{2}}}y=1\;}$

هر گاه دو خط مماس بیضی با هم زاویهٔ ۹۰° بسازند، نقطهٔ تقاطع آن دو خط مماس روی دایره‌ای قرار دارد که به دایره ارتوپتیک موسوم است و معادلهٔ آن عبارت است از:

${\displaystyle x^{2}+y^{2}=a^{2}+b^{2}}$

نیمساز زاویهٔ بین دو پاره‌خط ${\displaystyle {\overline {pf_{1}}}}$ و ${\displaystyle {\overline {pf_{2}}}}$ همواره بر خط مماس بیضی در نقطهٔ ${\displaystyle p}$ عمود است. از این ویژگی نتیجه می‌شود اگر اشعه‌ای از یکی از کانون‌ها به هر نقطه‌ای روی محیط بیضی بتابد به‌سوی کانون دیگر بازتاب می‌شود. این امر در نورپردازی و طراحی آکوستیک ساختمان‌ها کاربرد دارد.^[۷۲]

مساحت بیضی برابر است با:

${\displaystyle A_{\text{e}}=\pi ab}$

که در آن ${\displaystyle a}$ و ${\displaystyle b}$ به‌ترتیب نیم‌قطر بزرگ و نیم‌قطر کوچکند. فرمول مساحت بیضی را به‌سادگی می‌توان از فرمول مساحت دایره‌ای به شعاع ${\displaystyle b}$ (یعنی ${\displaystyle \pi b^{2}}$) به‌دست آورد. اگر دایره از یک طرف به نسبت ${\displaystyle a/b}$ کشیده شود، مساحت آن با در همین نسبت ضرب می‌شود: ${\displaystyle \pi b^{2}(a/b)=\pi ab}$.^[۷۳]

فرمول مساحت بیضی را با استفاده از انتگرال نیز می‌توان به‌سادگی محاسبه کرد. ابتدا معادلهٔ متعارف بیضی به صورت ${\displaystyle y(x)=b{\sqrt {1-x^{2}/a^{2}}}}$ بازنوشته می‌شود. برای هر ${\displaystyle x\in [-a,a]}$، این منحنی نیمهٔ بالایی بیضی است. پس مساحت بیضی دو برابر انتگرال ${\displaystyle y(x)}$ در بازهٔ ${\displaystyle [-a,a]}$ خواهد بود:^[۷۴]

${\displaystyle {\begin{aligned}A_{\text{e}}&=\int _{-a}^{a}2b{\sqrt {1-x^{2}/a^{2}}}\,dx\\&={\frac {b}{a}}\int _{-a}^{a}2{\sqrt {a^{2}-x^{2}}}\,dx={\frac {b}{a}}(\pi a^{2})=\pi ab\end{aligned}}}$

اگر معادلهٔ بیضی به‌شکل ${\displaystyle Ax^{2}+Bxy+Cy^{2}=1}$ نوشته شود، مساحت آن برابر ${\displaystyle {\frac {2\pi }{\sqrt {4AC-B^{2}}}}}$ خواهد بود.^[۷۵]

از آن‌جا که فرمولی با فرم بسته (مثل فرمول محیط دایره، که حالت خاص بیضی است) برای محیط بیضی وجود ندارد، مسئلهٔ بیان محیط دقیق بیضی منجر به ایجاد توابع بیضوی شد که موضوعی مهم در ریاضیات و فیزیک است.^[۷۶] برای محاسبه محیط بیضی، باید ابتدا انتگرال کامل بیضوی نوع دوم را محاسبه کرد. به این ترتیب محیط بیضی با نیم‌قطر بزرگ ${\displaystyle a}$ و نیم‌قطر کوچک ${\displaystyle b}$ برابر است با:^[۷۷]

${\displaystyle S(a,b)=4aE(e)}$،

که در آن ${\displaystyle e}$ همان برون‌مرکزی (${\displaystyle {\frac {c}{a}}={\frac {\sqrt {a^{2}-b^{2}}}{a}}}$) است و ${\displaystyle E}$ عبارت است از:

${\displaystyle E(e)=\int _{0}^{\pi /2}{\sqrt {1-e^{2}\sin ^{2}\theta }}\ d\theta }$

محیط بیضی بر اساس انتگرال کامل بیضوی نوع دوم را با استفاده از «سری گاوس-کومر»^[م] نیز می‌توان محاسبه کرد:^[۷۸]

${\displaystyle p=\pi (a+b)\sum _{n=0}^{\infty }{1/2 \choose n}^{2}h^{2n}}$

${\displaystyle =\pi (a+b)(1+{\frac {1}{4}}h^{2}+{\frac {1}{64}}h^{4}+{\frac {1}{256}}h^{6}+...)}$

بااین‌همه فرمول‌های پرشماری برای تخمین محیط بیضی ارائه شده که هر یک نقاط قوت و ضعف خود را دارند؛ مثلاً فرمول ابداعی سرینیواسا رامانوجان (۱۸۸۷ – ۱۹۲۰) برای تخمین محیط بیضی عبارت است از:^[۷۹]

${\displaystyle P\approx \pi [3(a+b)-{\sqrt {(3a+b)(a+3b)}}]}$

که برای بیضی‌هایی با برون‌مرکزی کم دقت بالایی دارد. یا راجر مارتنز^[ن] در سال ۲۰۰۰ فرمولی برای تخمین محیط بیضی ارائه داد که خطای آن همیشه کمتر از ۰٫۳۶۱۹٪ است:^[۸۰]

${\displaystyle P\approx 4a(1+(1-e^{2})^{y/2})^{1/y}}$

با این‌حال شناخته‌شده‌ترین فرمول تخمین محیط بیضی فرمولی است که اویلر در سال ۱۷۷۳ ارائه کرد:^[۸۱]

${\displaystyle P\approx \pi {\sqrt {2(a^{2}+b^{2})}}}$

انحنای بیضی برابر است با:^[۸۲]

${\displaystyle \kappa ={\frac {1}{a^{2}b^{2}}}\left({\frac {x^{2}}{a^{4}}}+{\frac {y^{2}}{b^{4}}}\right)^{-{\frac {3}{2}}}}$.

شعاع انحنا در نقطهٔ ${\displaystyle (x,y)}$ عبارت است از:^[۸۳]

${\displaystyle \rho =a^{2}b^{2}\left({\frac {x^{2}}{a^{4}}}+{\frac {y^{2}}{b^{4}}}\right)^{3/2}={\frac {1}{a^{4}b^{4}}}{\sqrt {\left(a^{4}y^{2}+b^{4}x^{2}\right)^{3}}}\ }$.

زاویه مماسی بیضی نیز از فرمول ${\displaystyle \phi (t)=tan^{-1}({\frac {a}{b}}\tan {t})}$ محاسبه می‌شود.^[۸۴]

خط قطبی هر نقطه روی بیضی، از خود آن نقطه می‌گذرد. همچنین قطب هر خط قطبی‌ای که بر بیضی مماس است روی آن بیضی است. این رابطهٔ متقابل قطب و خط قطبی در مقاطع مخروطی اساس تعریف این دو ویژگی است.^[۸۵] اگر معادلهٔ بیضی از معادلهٔ عام منحنی‌های درجهٔ دوم، یعنی به شکل:

${\displaystyle A_{xx}x^{2}+2A_{xy}xy+A_{yy}y^{2}+2B_{x}x+2B_{y}y+C=0}$

نوشته شود، معادلهٔ خط قطبی نقطهٔ ${\displaystyle (\xi ,\eta )}$ عبارت خواهد بود از:^[۸۶]

${\displaystyle Dx+Ey+F=0}$

که در آن ${\displaystyle D}$ و ${\displaystyle E}$ و ${\displaystyle F}$ ثابت‌هایی‌اند که به شکل زیر تعریف می‌شوند:

${\displaystyle {\begin{aligned}D&=A_{xx}\xi +A_{xy}\eta +B_{x}\\E&=A_{xy}\xi +A_{yy}\eta +B_{y}\\F&=B_{x}\xi +B_{y}\eta +C\,\end{aligned}}}$

با داشتن معادلهٔ خط قطبی ${\displaystyle (Dx+Ey+F=0)}$ نیز می‌توان قطب آن را با قرار دادن مقادیر ${\displaystyle x}$ و ${\displaystyle y}$ و ${\displaystyle z}$ از محاسبهٔ زیر در ${\displaystyle \left({\frac {x}{z}},{\frac {y}{z}}\right)}$ به‌دست آورد:^[۸۷]

${\displaystyle {\displaystyle {\begin{bmatrix}x\\y\\z\end{bmatrix}}={\begin{bmatrix}A_{xx}&A_{xy}&B_{x}\\A_{xy}&A_{yy}&B_{y}\\B_{x}&B_{y}&C\end{bmatrix}}^{-1}\cdot {\begin{bmatrix}D\\E\\F\end{bmatrix}}}}$

با چرخاندن بیضی به دور هر یک از قطرهایش، سطحی حاصل می‌شود که به گوی‌وار^[و] موسوم است.^[۸۸] گوی‌واری که از چرخش بیضی به دور قطر بزرگش حاصل شود «گوی‌وار کشیده»^[ه] و گوی‌واری که از چرخش بیضی به دور قطر کوچکش حاصل شود «گوی‌وار پَخ»^[ی] نام دارد.^[۸۹] با اکستروژن موازی بیضی «استوانهٔ بیضوی» و با اکستروژن مرکزی آن «مخروط بیضوی» ساخته می‌شود.

حجم‌هایی که همهٔ سطوح مقاطعشان به شکل بیضی باشد به بیضی‌وار موسومند. بیضی‌واری که در دو محورِ دستگاه مختصات دکارتی طولی مساوی داشته باشد گوی‌وار و بیضی‌واری که در هر سه محور طول مساوی داشته باشد کره است.^[۹۰]

ترسیم بیضی با ویژگی کانون آن به «روش باغبانی» موسوم است. در این روش دو قطعه چوب در دو نقطه از زمین (کانون‌ها) کوبیده می‌شود. حلقه طنابی به طول ${\displaystyle 2a+2c}$ که در نقطه‌ای از آن یک میله گره خورده‌است به دور دو قطعه چوب انداخته می‌شود و سپس میله جابجا می‌شود تا طناب کشیده شود. همهٔ نقاطی که میله را بتوان روی قرار داد به‌شکلی که طناب شل نباشد روی بیضی هستند.^[۹۱]

اگر دو رأس یک پاره‌خط را در راستای دو خط متقاطع حرکت دهیم، هر نقطهٔ ثابت روی آن پاره‌خط (یا امتداد آن) مکان هندسی کمانی از یک بیضی خواهد بود.^[۹۲] ترسیم بیضی با این روش به «روش خاگار (ترامل)»^[اا] موسوم است. در گذشته نیز ابزاری با نام «ترامل» برای ترسیم فنی و همچنین به‌عنوان اسباب‌بازی تولید می‌شد که دو پین قابل تنظیم و یک گیره (برای اتصال قلم) داشت و با استفاده از آن می‌شد بیضی رسم کرد.^[۹۳]

روش متوازی‌الأضلاع یا تولید مخروطی اشتاینر را می‌توان زمان داشتن قطرهای بیضی یا یک وتر و قطر مزدوج آن به کار برد. در این روش یک متوازی‌الأضلاع (در تصویر مجاور ${\displaystyle ABV_{1}V_{2}}$) به مرکزیت نقطهٔ ${\displaystyle P}$ در نظر گرفته می‌شود به صورتی که هر کدام از اضلاع آن مساوی و موازی یکی از قطرهای بیضی (یا یک وتر و قطر مزدوجش) باشند. ضلع‌های ${\displaystyle {\overline {AB}}}$ و ${\displaystyle {\overline {V_{1}B}}}$ به ${\displaystyle n}$ پاره‌خط مساوی تقسیم می‌شوند. سپس از رأس ${\displaystyle V_{1}}$ به سر هر کدام از پاره‌خط‌های روی ضلع ${\displaystyle {\overline {AB}}}$ و از رأس ${\displaystyle V_{2}}$ به سر هر کدام از پاره‌خط‌های روی ضلع ${\displaystyle {\overline {V_{1}B}}}$ پاره‌خطی کشیده می‌شود. نقطهٔ تقاطع پاره‌خط‌های ${\displaystyle V_{1}B_{i}}$ و ${\displaystyle V_{1}B_{i}}$ روی بیضی قرار دارد.^[۹۴]

می‌توان با داشتن دو قطر بیضی، و با استفاده از پرگار شکلی تقریبی از بیضی ترسیم کرد. برای این منظور روی پاره‌خط AD، که انتهای قطرهای کوچک و بزرگ را به هم وصل می‌کند، نقطهٔ F در فاصله DF = b - a (تفاضل نیم‌قطرها) قرار داده می‌شود. از وسط AF خطی عمود خارج می‌شود که قطر بزرگ را در نقطهٔ ${\displaystyle G}$ و قطر کوچک (یا امتداد آن را) در ${\displaystyle H}$ قطع می‌کند. سپس با استفاده از تقارن (بازتاب ${\displaystyle G}$ و ${\displaystyle H}$ روی قطرها) نقاط ${\displaystyle G'}$ و ${\displaystyle H'}$ مشخص می‌شوند. با زدن کمان‌هایی متصل به مرکز هر کدام از نقاط ${\displaystyle G}$ و ${\displaystyle H}$ و ${\displaystyle G'}$ و ${\displaystyle H'}$ شکل تقریبی بیضی را مشخص کرد.^[۹۵]