Algorithme de tracé de segment de Bresenham — Wikipédia
L’algorithme de tracé de segment de Bresenham est un algorithme développé par Jack E. Bresenham en , alors qu’il travaillait dans un laboratoire informatique d’IBM et cherchait à piloter un traceur attaché à une console texte. Cet algorithme a été présenté à la convention de l’ACM en 1963, puis publié en 1965 dans la revue IBM Systems Journal.
L’algorithme détermine quels sont les points d’un plan discret qui doivent être tracés afin de former une approximation de segment de droite entre deux points donnés. Cet algorithme est souvent utilisé pour dessiner des segments de droites sur l’écran d’un ordinateur ou une image calculée pour l’impression. Il est considéré comme l’un des premiers algorithmes découverts dans le domaine de la synthèse d'image [1].
Utilisations
[modifier | modifier le code]Le principe du calcul est largement documenté et a depuis été repris pour tracer de façon incrémentale n’importe quelle courbe conique (cercle, ellipse, arc, parabole, hyperbole) ou courbes de Bézier grâce aux propriétés de leur fonction polynomiale de définition, dont les dérivées permettent de calculer les orientations de segments élémentaires avec de simples opérations entières. On peut même l’adapter à l’approximation de courbes dont on ne connaît qu’un développement limité (dont on ne prendra que les premiers termes de faible degré), utilisable avec une bonne précision sur un domaine suffisant par rapport à la résolution (sinusoïdes, exponentielles, puissances non entières).
L’algorithme est également facilement adaptable au calcul de courbes et surfaces dans un espace discret de plus de 2 dimensions (notamment pour le pilotage de machines-outils). Même en deux dimensions seulement, on peut discrétiser avec cet algorithme une courbe avec une fonction de lissage prenant en compte l’erreur commise entre deux points candidats afin d’ajuster leur couleur, l’erreur incrémentale étant convertible en coefficient de transparence, ce qui permet de conserver la graisse (épaisseur visuelle) d’une courbe tout en limitant l’effet d’escalier (crénelage).
Cet algorithme intervient aussi dans le lissage de rendus de textures 2D appliquées sur des surfaces d’une scène 3D où la texture subit des réductions ou agrandissements. On l’emploie aussi pour le lissage d’agrandissements photographiques, ou pour l’interpolation de couleurs intermédiaires sur une échelle discrète.
Explication de l’algorithme de base dans le premier octant
[modifier | modifier le code]
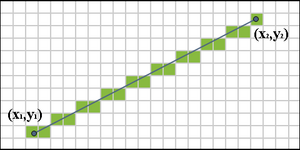
La ligne est tracée entre deux points (x1, y1) et (x2, y2), où chaque paire indique la colonne et la rangée, respectivement, croissant vers la droite et le bas. On supposera au départ que notre segment descend vers le bas et la droite, et que la distance horizontale x2–x1 excède la distance verticale y2–y1 (c’est-à-dire que le segment a une pente comprise entre 0 et -1). Notre but est, pour chaque colonne x entre x1 et x2, d’identifier la rangée y dans cette colonne qui est la plus proche du segment idéal et de tracer un pixel en (x, y).
Détermination des ordonnées
[modifier | modifier le code]Il s'agit maintenant de déterminer quel pixel est le plus proche de la droite pour une colonne donnée. La formule générale d’une droite entre les deux points est donnée par :
- . (1)
Puisque la colonne est connue, la rangée du pixel le plus proche de l’ordonnée exacte du point d’abscisse sur la droite est donnée en arrondissant cette ordonnée y à l’entier le plus proche :
- . (2)
La valeur 0,5 dans le membre de droite est une approximation des coordonnées (le point est au milieu du carré).
Cependant, le calcul explicite de cette valeur pour chaque colonne est coûteux. Or commence en , et que chaque fois qu'on ajoute 1 à l'abscisse, on ajoute la valeur constante à la valeur de l’ordonnée y du point de la droite correspondant. Cette valeur est la pente de la droite, et en vertu de notre hypothèse initiale, elle est comprise entre 0 et -1. Après l’arrondi, pour chaque colonne , on utilise donc soit la valeur précédente (ordonnée du pixel d'abscisse ), soit cette valeur augmentée de 1.
On peut décider laquelle de ces deux valeurs prendre en conservant une valeur d’erreur qui représente la distance verticale entre la valeur courante et la valeur y exacte pour la droite à l’abscisse courante. Au départ cette valeur d’erreur e est nulle et chaque fois qu'on incrémente , on augmente la valeur d’erreur par la valeur de pente ci-dessus. Chaque fois que l’erreur dépasse 0,5, la droite est devenue plus proche de la valeur suivante, aussi on ajoute 1 à en retranchant simultanément 1,0 à l’erreur e.
La procédure ressemble à ceci, en supposant que tracerPixel(x, y) est une primitive graphique traçant le pixel de rangée x et de colonne y ; exprimé en pseudo-code, l’algorithme de base est :
procédure tracerSegment(entier x1, entier y1, entier x2, entier y2) est déclarer entier x, y, dx, dy ; déclarer rationnel e, e(1,0), e(0,1) ; // valeur d’erreur et incréments dy ← y2 - y1 ; dx ← x2 - x1 ; y ← y1 ; // rangée initiale e ← 0,0 ; // valeur d’erreur initiale e(1,0) ← dy / dx ; e(0,1) ← -1.0 ; pour x variant de x1 jusqu’à x2 par incrément de 1 faire tracerPixel(x, y) ; si (e ← e + e(1,0)) ≥ 0,5 alors // erreur pour le pixel suivant de même rangée y ← y + 1 ; // choisir plutôt le pixel suivant dans la rangée supérieure e ← e + e(0,1) ; // ajuste l’erreur commise dans cette nouvelle rangée fin si ; fin pour ; fin procédure ;
Amélioration de l’algorithme pour le calcul avec des entiers
[modifier | modifier le code]Le problème avec cet algorithme simple est que les microprocesseurs d’ordinateur sont relativement lents dans le calcul sur des nombres en virgule flottante (et la représentation suggérée ci-dessus sous forme de nombres rationnels pour e et e(1,0) est nettement plus complexe et non nativement prise en charge par les processeurs ce qui augmente le nombre d’instructions pour travailler sur de tels nombres) ; de plus, les erreurs d’approximation du nombre flottant e(1,0) s’accumulent à chaque addition de e(1,0) dans e. Travailler avec uniquement des entiers permettrait un calcul à la fois plus exact et plus rapide.
La première astuce est de remarquer d’abord qu’on peut remplacer e par e–0,5, ce qui permet de ne tester que le signe de la valeur d’erreur au lieu de comparer deux rationnels, le test de proximité par rapport à la droite exacte revient alors à savoir lequel des deux pixels candidats se situe en dessous de la droite exacte parallèle dont les ordonnées sont augmentées de 0,5, et de remplacer l’arrondi de la formule (1) ci-dessus à l’entier le plus proche par un arrondi à l’entier égal ou inférieur avec cette nouvelle droite, ce qui ne change effectivement pas la formule (2) ci-dessus, mais e représentera l’erreur commise lors de l'approximation de cette seconde droite par les pixels tracés :
procédure tracerSegment(entier x1, entier y1, entier x2, entier y2) est déclarer entier x, y, dx, dy ; déclarer rationnel e, e(1,0), e(0,1) ; // valeur d’erreur et incréments dy ← y2 - y1 ; dx ← x2 - x1 ; y ← y1 ; // rangée initiale e ← -0,5 ; // valeur d’erreur initiale e(1,0) ← dy / dx ; e(0,1) ← -1.0 ; pour x variant de x1 jusqu’à x2 par incrément de 1 faire tracerPixel(x, y) ; si (e ← e + e(1,0)) ≥ 0 alors // erreur pour le pixel suivant de même rangée y ← y + 1 ; // choisir plutôt le pixel suivant dans la rangée supérieure e ← e + e(0,1) ; // ajuste l’erreur commise dans cette nouvelle rangée fin si ; fin pour ; fin procédure ;
Ensuite en multipliant tous les rationnels ci-dessus par dx, le calcul ne demande plus d’incréments rationnels (ce qui élimine l'accumulation d'erreurs d’approximation des flottants). Cependant la valeur initiale de e= –0,5×dx n’est pas encore entière, même si ses incréments sont entiers.
procédure tracerSegment(entier x1, entier y1, entier x2, entier y2) est déclarer entier x, y, dx, dy ; déclarer rationnel e ; // valeur d’erreur déclarer entier e(1,0), e(0,1) ; // incréments dy ← y2 - y1 ; dx ← x2 - x1 ; y ← y1 ; // rangée initiale e ← -0,5 × dx ; // valeur d’erreur initiale e(1,0) ← dy ; e(0,1) ← -dx ; pour x variant de x1 jusqu’à x2 par incrément de 1 faire tracerPixel(x, y) ; si (e ← e + e(1,0)) ≥ 0 alors // erreur pour le pixel suivant de même rangée y ← y + 1 ; // choisir plutôt le pixel suivant dans la rangée supérieure e ← e + e(0,1) ; // ajuste l’erreur commise dans cette nouvelle rangée fin si ; fin pour ; fin procédure ;
Toutefois en doublant e (et les valeurs de ses incréments), cela ne change rien au test de son signe : e représentera alors la distance par rapport à la droite exacte d’ordonnées augmentées de 0,5, cette distance étant multipliée par le facteur constant positif 2×dy (ce qui ne change pas le signe de la valeur d’erreur testée). La valeur de pente utilisée comme incrément de e étant aussi multipliée par le même facteur devient simplement 2×dy, sa valeur initiale devient –dx, le second décrément conditionnel devient 2×dx (que l’on peut aussi précalculer). L’algorithme devient alors :
procédure tracerSegment(entier x1, entier y1, entier x2, entier y2) est déclarer entier x, y, dx, dy ; déclarer entier e ; // valeur d’erreur déclarer entier e(1,0), e(0,1) ; // incréments dy ← y2 - y1 ; dx ← x2 - x1 ; y ← y1 ; // rangée initiale e ← -dx ; // valeur d’erreur initiale e(1,0) ← dy × 2 ; e(0,1) ← -dx × 2; pour x variant de x1 jusqu’à x2 par incrément de 1 faire tracerPixel(x, y) ; si (e ← e + e(1,0)) ≥ 0 alors // erreur pour le pixel suivant de même rangée y ← y + 1 ; // choisir plutôt le pixel suivant dans la rangée supérieure e ← e + e(0,1) ; // ajuste l’erreur commise dans cette nouvelle rangée fin si ; fin pour ; fin procédure ;
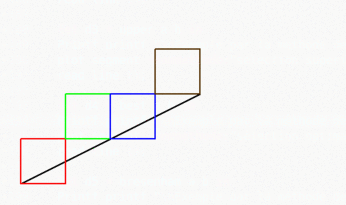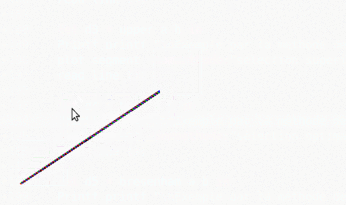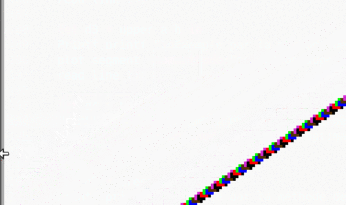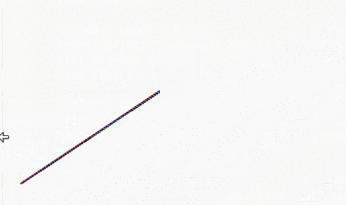
Réduction des variables et simplifications
[modifier | modifier le code]On pourra enfin changer le signe de e en testant le signe opposé, puis réduire le nombre de variables, en constatant que x1 et y1 ci-dessus ne sont plus utilisés dès que l’erreur initiale et les incréments sont calculés ; il suffit de changer aussi le signe des incréments et décréments :
procédure tracerSegment(entier x1, entier y1, entier x2, entier y2) est déclarer entier dx, dy ; déclarer entier e ; // valeur d’erreur e ← x2 - x1 ; // -e(0,1) dx ← e × 2 ; // -e(0,1) dy ← (y2 - y1) × 2 ; // e(1,0) tant que x1 ≤ x2 faire tracerPixel(x1, y1) ; x1 ← x1 + 1 ; // colonne du pixel suivant si (e ← e - dy) ≤ 0 alors // erreur pour le pixel suivant de même rangée y1 ← y1 + 1 ; // choisir plutôt le pixel suivant dans la rangée supérieure e ← e + dx ; // ajuste l’erreur commise dans cette nouvelle rangée fin si ; fin faire ; // Le pixel final (x2, y2) n’est pas tracé. fin procédure ;
Cet algorithme est optimal et suffisant pour tracer tout vecteur horizontal diagonal ou oblique dans le premier octant, de colonnes et rangées croissantes. Si le langage de programmation le permet, les deux variables locales déclarées x et y peuvent être remplacées par réutilisation des variables x1 et y1 des paramètres. Ce cas est traité ci-dessus.
Toutefois il faut remarquer dans l’algorithme ci-dessus que le test du signe de e peut aussi bien inclure l’égalité avec zéro ou ne pas l’inclure. Cela correspond au fait que les deux pixels suivants candidats sont équidistants de la droite exacte. Si on choisit un déplacement diagonal le deuxième point suivant sera toujours obtenu par un déplacement horizontal ; si on choisit un déplacement horizontal le deuxième point suivant sera toujours obtenu par un déplacement diagonal. Si on inversait la direction du vecteur, les pixels choisis seraient inversés donc différents, et on devra en tenir compte si on souhaite un recouvrement exact des pixels de deux vecteurs obliques de sens opposés, lors de la généralisation de l’algorithme à des vecteurs obliques de directions quelconques (ce cas ne peut pas se produire pour le tracé de vecteurs horizontaux, verticaux ou diagonaux).
Algorithme général optimisé
[modifier | modifier le code]La généralisation de l’algorithme de base au tracé de vecteurs de direction quelconque est obtenue par simple symétrie.
L’algorithme est ici développé et optimisé dans chacun des huit octants. Toutefois, afin de s’assurer que les mêmes pixels seront toujours tracés pour deux vecteurs identiques mais de direction opposée, on inversera les cas limites où un déplacement diagonal est à égalité avec un déplacement droit, en choissant la diagonale quand le vecteur est orienté vers la gauche (abscisses décroissantes) plutôt que vers la droite (abscisses croissantes) comme dans le cas simplifié ci-dessus :
procédure tracerSegment(entier x1, entier y1, entier x2, entier y2) est déclarer entier dx, dy; si (dx ← x2 - x1) ≠ 0 alors si dx > 0 alors si (dy ← y2 - y1) ≠ 0 alors si dy > 0 alors // vecteur oblique dans le 1er quadrant si dx ≥ dy alors // vecteur diagonal ou oblique proche de l’horizontale, dans le 1er octant déclarer entier e ; dx ← (e ← dx) × 2 ; dy ← dy × 2 ; // e est positif boucle sans fin // déplacements horizontaux tracePixel(x1, y1) ; interrompre boucle si (x1 ← x1 + 1) = x2 ; si (e ← e - dy) < 0 alors y1 ← y1 + 1 ; // déplacement diagonal e ← e + dx ; fin si ; fin boucle ; sinon // vecteur oblique proche de la verticale, dans le 2d octant déclarer entier e ; dy ← (e ← dy) × 2 ; dx ← dx × 2 ; // e est positif boucle sans fin // déplacements verticaux tracePixel(x1, y1) ; interrompre boucle si (y1 ← y1 + 1) = y2 ; si (e ← e - dx) < 0 alors x1 ← x1 + 1 ; // déplacement diagonal e ← e + dy ; fin si ; fin boucle ; fin si ; sinon // dy < 0 (et dx > 0) // vecteur oblique dans le 4e quadrant si dx ≥ -dy alors // vecteur diagonal ou oblique proche de l’horizontale, dans le 8e octant déclarer entier e ; dx ← (e ← dx) × 2 ; dy ← dy × 2 ; // e est positif boucle sans fin // déplacements horizontaux tracePixel(x1, y1) ; interrompre boucle si (x1 ← x1 + 1) = x2 ; si (e ← e + dy) < 0 alors y1 ← y1 - 1 ; // déplacement diagonal e ← e + dx ; fin si ; fin boucle ; sinon // vecteur oblique proche de la verticale, dans le 7e octant déclarer entier e ; dy ← (e ← dy) × 2 ; dx ← dx × 2 ; // e est négatif boucle sans fin // déplacements verticaux tracePixel(x1, y1) ; interrompre boucle si (y1 ← y1 - 1) = y2 ; si (e ← e + dx) > 0 alors x1 ← x1 + 1 ; // déplacement diagonal e ← e + dy ; fin si ; fin boucle ; fin si ; fin si ; sinon // dy = 0 (et dx > 0) // vecteur horizontal vers la droite répéter tracePixel(x1, y1) ; jusqu’à ce que (x1 ← x1 + 1) = x2 ; fin si ; sinon // dx < 0 si (dy ← y2 - y1) ≠ 0 alors si dy > 0 alors // vecteur oblique dans le 2d quadrant si -dx ≥ dy alors // vecteur diagonal ou oblique proche de l’horizontale, dans le 4e octant déclarer entier e ; dx ← (e ← dx) × 2 ; dy ← dy × 2 ; // e est négatif boucle sans fin // déplacements horizontaux tracePixel(x1, y1) ; interrompre boucle si (x1 ← x1 - 1) = x2 ; si (e ← e + dy) ≥ 0 alors y1 ← y1 + 1 ; // déplacement diagonal e ← e + dx ; fin si ; fin boucle ; sinon // vecteur oblique proche de la verticale, dans le 3e octant déclarer entier e ; dy ← (e ← dy) × 2 ; dx ← dx × 2 ; // e est positif boucle sans fin // déplacements verticaux tracePixel(x1, y1) ; interrompre boucle si (y1 ← y1 + 1) = y2 ; si (e ← e + dx) ≤ 0 alors x1 ← x1 - 1 ; // déplacement diagonal e ← e + dy ; fin si ; fin boucle ; fin si ; sinon // dy < 0 (et dx < 0) // vecteur oblique dans le 3e quadrant si dx ≤ dy alors // vecteur diagonal ou oblique proche de l’horizontale, dans le 5e octant déclarer entier e ; dx ← (e ← dx) × 2 ; dy ← dy × 2 ; // e est négatif boucle sans fin // déplacements horizontaux tracePixel(x1, y1) ; interrompre boucle si (x1 ← x1 - 1) = x2 ; si (e ← e - dy) ≥ 0 alors y1 ← y1 - 1 ; // déplacement diagonal e ← e + dx ; fin si ; fin boucle ; sinon // vecteur oblique proche de la verticale, dans le 6e octant déclarer entier e ; dy ← (e ← dy) × 2 ; dx ← dx × 2 ; // e est négatif boucle sans fin // déplacements verticaux tracePixel(x1, y1) ; interrompre boucle si (y1 ← y1 - 1) = y2 ; si (e ← e - dx) ≥ 0 alors x1 ← x1 - 1 ; // déplacement diagonal e ← e + dy ; fin si ; fin boucle ; fin si ; fin si ; sinon // dy = 0 (et dx < 0) // vecteur horizontal vers la gauche répéter tracePixel(x1, y1) ; jusqu’à ce que (x1 ← x1 - 1) = x2 ; fin si ; fin si ; sinon // dx = 0 si (dy ← y2 - y1) ≠ 0 alors si dy > 0 alors // vecteur vertical croissant répéter tracePixel(x1, y1) ; jusqu’à ce que (y1 ← y1 + 1) = y2 ; sinon // dy < 0 (et dx = 0) // vecteur vertical décroissant répéter tracePixel(x1, y1) ; jusqu’à ce que (y1 ← y1 - 1) = y2 ; fin si ; fin si ; fin si ; // le pixel final (x2, y2) n’est pas tracé. fin procédure ;
Notes :
- Ci-dessus, les affectations sont parfois regroupées au sein des expressions qui en réutilisent la valeur affectée. Si le langage utilisé ne le permet pas, il suffit d'effectuer les affectations internes dans des instructions d’affectation préalables séparées, et de relire cette variable dans l’expression contenante.
- Les primitives graphiques tracePixel(x1, y1) sont regroupées ci-dessus pour tracer dans la boucle interne des segments horizontaux (cas du premier octant ci-dessus) ou verticaux (second octant), et peuvent être regroupées en un seul appel (il suffit de compter le nombre de passages dans la boucle interne, et d’effectuer le tracé de segment horizontal (ou vertical) en sortie de cette boucle.
Références
[modifier | modifier le code]- James D. Foley, Introduction à l'infographie, Paris, Addison-Wesley France, , 573 p. (ISBN 978-2-87908-058-1, BNF 37480856), p.76 à 84
- (en) Jack E. Bresenham, « Algorithm for computer control of a digital plotter », IBM Systems Journal, vol. 4, no 1, , p. 25–30 (DOI 10.1147/sj.41.0025, lire en ligne)


 French
French Deutsch
Deutsch








