Golygone — Wikipédia
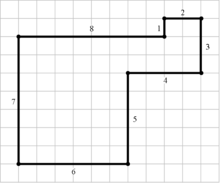
Un golygone est un polygone ne possédant que des angles droits, dont la longueur des côtés est une suite d'entiers consécutifs.
Propriétés
[modifier | modifier le code]Un golygone est un isogone à 90° sériel, c'est-à-dire un polygone dont les angles sont égaux (ici, des angles droits) et dont les longueurs des côtés sont des nombres entiers consécutifs. En partant d'un sommet origine, le second sommet d'un golygone est situé à une unité de distance du premier sommet en direction du nord ou du sud, le troisième à deux unités du deuxième en direction de l'ouest ou de l'est, le quatrième à trois unités du troisième vers le nord ou le sud, et ainsi de suite jusqu'à retourner au sommet origine.
Dans un tel polygone, la longueur de tous les côtés horizontaux ont même parité, de même que tous les côtés verticaux. Ainsi, le nombre n de côtés d'un golygone doit satisfaire les deux équations suivantes :
- ± 1 ± 3 ... ± (n-1) = 0
- ± 2 ± 4 ... ± n = 0
Il s'ensuit que n doit être un multiple de 8[1].
Il existe un unique golygone à huit côtés ; il n'est pas croisé et peut paver le plan par rotation de 180°[2]. Il existe 28 golygones à 16 côtés, dont seuls 3 ne sont pas croisés[2], 2 108 à 24 côtés, 227 322 à 32 côtés, etc.[2],[3] Le nombre de golygones d'un certain ordre peut être facilement calculé ; en revanche, déterminer le nombre de golygones non-croisés est un problème nettement plus difficile.
Il est possible de varier la définition en utilisant d'autres suites de nombres que des entiers consécutifs, ou d'autres angles que 90°[1].
Historique
[modifier | modifier le code]Les golygones sont inventés et nommés par Lee Sallows (en)[4],[1], et popularisés par Alexander Dewdney (en) en 1990 dans un article du Scientific American[5].
Annexes
[modifier | modifier le code]Liens internes
[modifier | modifier le code]Références
[modifier | modifier le code]- (en) Lee Sallows, « New pathways in serial isogons », The Mathematical Intelligencer, vol. 14, no 2, , p. 55–67 (DOI 10.1007/BF03025216).
- (en) Lee Sallows, Martin Gardner, Richard Guy et Donald Knuth, « Serial isogons of 90 degrees », Mathematics Magazine, vol. 64, no 5, , p. 315–324 (DOI 10.2307/2690648, JSTOR 2690648).
- (en) « Golygons », Encyclopédie en ligne des suites de nombres entiers.
- (en) Harry J. Smith, « What is a Golygon? ».
- (en) Alexander Keewatin Dewdney, « An odd journey along even roads leads to home in Golygon City », Scientific American, vol. 263, , p. 118–121.


 French
French Deutsch
Deutsch