Intersection conique — Wikipédia

Intersection conique idéale entre deux surfaces d'énergie potentielle. Les axes horizontaux représentent les positions nucléaires, l'axe vertical est l'énergie des deux états possibles.

En chimie quantique, une intersection conique de deux surfaces d'énergie potentielle (SEP) de mêmes symétries spatiales et de spin est l'ensemble des points géométriques où deux SEP sont dégénérées (se croisent)[1]. Les intersections coniques se rencontrent dans tous les systèmes chimiques triviaux et non triviaux.

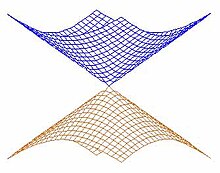
Dans un système à deux coordonnées, ce phénomène peut se produire pour une géométrie donnée. Si les SEP sont tracées comme des fonctions des deux coordonnées, elles forment un cône centré sur le point de dégénérescence. Cela est montré sur la figure de droite, les SEP inférieure et supérieure ayant deux couleurs différentes. Le nom d'intersection conique provient de cette observation.

De manière plus générale, on trouve des intersections coniques lorsque pour une même géométrie, il existe deux états électroniques de même énergie et que ces systèmes n'interagissent pas entre eux[note 1]. En termes d'hamiltonien effectif ne tenant compte que de ces deux états et de leur possible interaction, les termes diagonaux sont identiques et les termes non-diagonaux sont nuls. Généralement, les systèmes chimiques ont un nombre élevé de degrés de liberté. Pour un système à n coordonnées, les points dégénérés sont inclus dans l'espace d'intersection, ou « jointure »[note 2], de dimension n-2. Les deux dimensions restantes définissant l'intersection (dégénérescence énergétique) du système définissent l'« espace de bifurcation ».

Les intersections coniques sont aussi appelées « (doubles) entonnoirs moléculaires » ou « points diaboliques ». Ces dénominations ne sont pas seulement dues à la forme géométrique de leurs représentations, mais aussi en raison de l'importance cruciale des transitions non-radiatives[note 3] très rapides d'états électroniques excités vers des états moins énergétiques qui passent par ces points.

Les intersections coniques sont directement liées au couplage vibronique et à l'effet Jahn-Teller. Elles interviennent, comme l'ont montré de nombreuses expériences, dans les processus photochimiques de molécules organiques, ainsi que dans les systèmes biologiques[2]. Ainsi, la stabilité de l'ADN sous irradiation UV est imputable à une intersection conique. Le paquet d'onde moléculaire excité dans un état d'énergie donné par le photon UV suit la courbe de la SEP, et atteint l'intersection conique par le dessus. À ce moment, le couplage vibronique très important induit une transition non-radiative (surface-hopping : saut en surface) qui ramène la molécule dans son état fondamental.

Notes et références

[modifier | modifier le code]

Notes

[modifier | modifier le code]
  1. ↑ S'il y a interaction, on a un croisement évité, ce qui peut donner une transition de Landau-Zener
  2. ↑ De l'anglais seam, littéralement couture.
  3. ↑ Ce qui est différent des transitions verticales prédites par le principe de Franck-Condon.

Références

[modifier | modifier le code]
  1. ↑ (es) Isabel Gomez Lara, Estudio AB initio de mecanismos de reacción en sistemas moleculares fotosensibles (Thèse de doctorat), (lire en ligne) (a servi de source générale à la version originale de l'article en espagnol, sauf indication contraire et a également servi de bibliographie additionnelle).
  2. ↑ (en) Worth, G.A.; Cederbaum, L.S., « Beyond Born-Oppenheimer: Molecular Dynamics Through a Conical Intersection », Annu. Rev. Phys. Chem, vol. 55,‎ , p. 127-158

Annexes

[modifier | modifier le code]

Bibliographie

[modifier | modifier le code]
  • (en) Diabolical Conical Intersections, David Yarkony, Rev. Mod. Phys. 68, 985-1013 (1996).
  • (en) Beyond Born-Oppenheimer: Electronic Nonadiabatic Coupling Terms and Conical Intersections de Michael Baer (Wiley-Interscience, 2006).

Lien externe

[modifier | modifier le code]
Ce document provient de « https://fr.wikipedia.org/w/index.php?title=Intersection_conique&oldid=206645940 ».