Surapprentissage — Wikipédia

Pour l’article homonyme, voir Surapprentissage (psychologie)Surapprentissage (psychologie).

Cet article ne cite pas suffisamment ses sources (avril 2019).

Si vous disposez d'ouvrages ou d'articles de référence ou si vous connaissez des sites web de qualité traitant du thème abordé ici, merci de compléter l'article en donnant les références utiles à sa vérifiabilité et en les liant à la section « Notes et références ».

En pratique : Quelles sources sont attendues ? Comment ajouter mes sources ?

En statistique, le surapprentissage, ou surajustement ou encore surinterprétation, est une analyse statistique qui correspond trop précisément à une collection particulière d'un ensemble de données. Ainsi, cette analyse peut ne pas correspondre à des données supplémentaires ou ne pas prévoir de manière fiable les observations futures. Un modèle surajusté est un modèle statistique qui contient plus de paramètres que ne peuvent le justifier les données^[1].

Le problème existe aussi en apprentissage automatique ^[2]. Il est en général provoqué par un mauvais dimensionnement de la structure utilisée pour classifier ou faire une régression. De par sa trop grande capacité à capturer des informations, une structure dans une situation de surapprentissage aura de la peine à généraliser les caractéristiques des données. Elle se comporte alors comme une table contenant tous les échantillons utilisés lors de l'apprentissage et perd ses pouvoirs de prédiction sur de nouveaux échantillons.

Le surapprentissage s'interprète comme un apprentissage « par cœur » des données, un genre de mémorisation. Il résulte souvent d'une trop grande liberté dans le choix du modèle.

La figure ci-dessous illustre ce phénomène dans le cas d'une régression dans ${\displaystyle \mathbb {R} ^{2}}$.

Les points verts sont correctement décrits par une régression linéaire.

Si l'on autorise un ensemble de fonctions d'apprentissage plus grand, par exemple l'ensemble des fonctions polynomiales à coefficients réels, il est possible de trouver un modèle décrivant parfaitement les données d'apprentissage (erreur d'apprentissage nulle). C'est le cas du polynôme d'interpolation de Lagrange : il passe bien par tous les points verts mais n'a visiblement aucune capacité de généralisation.

Pour limiter ce genre de problèmes dans le cas des réseaux de neurones, on doit veiller à utiliser un nombre adéquat de paramètres et donc de neurones et de couches cachées. Il est recommandé de débuter avec des modèles simples avec moins de paramètres en première approche. Cependant, ces paramètres optimaux sont difficiles à déterminer à l'avance.

Pour détecter un surapprentissage, on sépare les données en k sous-ensembles : k-1 ensembles d'apprentissage et un ensemble de validation. L'ensemble d'apprentissage comme son nom l'indique permet d'entraîner et faire évoluer les poids du modèle. L'ensemble de validation est utilisé pour vérifier la pertinence du réseau et de ses paramètres. Ce processus est répété k fois en changeant l'ensemble de validation à chaque fois.

On peut vraisemblablement parler de surapprentissage si l'erreur de prédiction du réseau sur l'ensemble d'apprentissage diminue alors que l'erreur sur la validation augmente de manière significative. Cela signifie que le réseau continue à améliorer ses performances sur les échantillons d'apprentissage mais perd son pouvoir de généralisation et de prédiction sur ceux provenant de la validation.

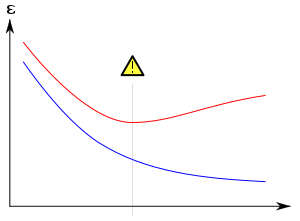
Pour avoir un réseau qui généralise bien, on arrête l'apprentissage dès que l'on observe cette divergence entre les deux courbes. On peut aussi diminuer la taille du réseau et recommencer l'apprentissage. Les méthodes de régularisation comme le weight decay permettent également de limiter la spécialisation.

Une autre méthode permettant d'éviter le surapprentissage est d'utiliser une forme de régularisation. Durant l'apprentissage, on pénalise les valeurs extrêmes des paramètres, car ces valeurs correspondent souvent à un surapprentissage.

D'autres méthodes pour éviter le surapprentissage existent. Elles dépendent beaucoup du problème que l'on doit résoudre ainsi que du type de données traitées. En plus de celles déjà citées, voici les autres méthodes^[3] qui peuvent donner de bons résultats :

• ajouter des données ;
• réduire le nombre de caractéristiques, par sélection ou extraction ;
• augmentation de données ;
• arrêt précoce en apprentissage profond ;
• commencer avec un choix de modèle simple ;
• ajouter du bruit aux données ;
• assembler plusieurs modèles.

• Rasoir d'Ockham pour des phénomènes semblables au surapprentissage dans d'autres domaines.
• Ajustement de courbe
• Data dredging
• Abandon (réseaux neuronaux), une technique pour éviter le surapprentissage

• Portail de l'informatique théorique
• Portail des probabilités et de la statistique