Théorie du champ moléculaire — Wikipédia

Cet article ne cite pas suffisamment ses sources (mai 2018).

Si vous disposez d'ouvrages ou d'articles de référence ou si vous connaissez des sites web de qualité traitant du thème abordé ici, merci de compléter l'article en donnant les références utiles à sa vérifiabilité et en les liant à la section « Notes et références ».

En pratique : Quelles sources sont attendues ? Comment ajouter mes sources ?

Le champ moléculaire est un modèle développé par Pierre Weiss dans l’objectif de fonder une théorie du comportement des ferromagnétiques. Cette théorie est ensuite étendue à d'autres matériaux magnétiques.

Certains matériaux, en particulier les ferromagnétiques, possèdent une aimantation spontanée en l'absence de tout champ magnétique externe. Ce modèle explique l'existence de cette aimantation par l'action d'un champ interne nommé champ moléculaire. Le champ moléculaire traduit l'interaction mutuelle de moments magnétiques atomiques qui s'alignent dans la matière pour minimiser leur interaction d'échange. Lorsque la température augmente, l'agitation thermique devient le mécanisme d'action dominant et désordonne progressivement l'orientation des moments magnétiques atomiques. L'aimantation disparaît lorsque l'on s'approche de la température de Curie. Une fois cette température dépassée, le matériau devient paramagnétique.

Les travaux de Weiss ayant amené à la réalisation du modèle du champ moléculaire s’appuient principalement sur les découvertes effectuées avant lui par Pierre Curie et Paul Langevin. Il s’est appuyé sur les publications de Langevin sur la théorie électronique du diamagnétisme et la théorie cinétique du paramagnétisme. Ces publications rendent elles-mêmes compte de la loi de Curie :

${\displaystyle {\displaystyle \chi _{m}={\frac {C}{T-T_{c}}}}}$,

où ${\displaystyle X_{m}}$ correspond à la susceptibilité magnétique, ${\displaystyle T_{c}}$ à la température de Curie et ${\displaystyle C}$ à la constante de Curie.

Langevin considère que l'ensemble des moments magnétiques du milieu paramagnétique se comporte selon la thermodynamique statistique de Ludwig Boltzmann sans tenir compte de leurs interactions mutuelles.

En 1907, Weiss postule qu’il existe une interaction qu’il modélise à l’aide d'un champ intérieur ${\displaystyle H_{m}}$ proportionnel à l’aimantation. Ce champ sera par la suite renommé champ moléculaire.Ce modèle a permis de décrire de manière phénoménologique les fortes interactions qui existent entre les moments magnétiques.

C'est en 1928 que fut pour la première expliquée l'origine microscopique du champ moléculaire par Heisenberg. Ce dernier montra que l'interaction d'échange est à l'origine du fort couplage entre les moments magnétiques ^[1].

En 1959, soit 50 ans après la création du modèle du champ moléculaire de Weiss, Louis Néel introduit la notion de champ moléculaire local, en donnant ainsi la clé des propriétés des corps antiferromagnétiques et ferrimagnétiques. Dans les exemples traités par Weiss, la théorie du champ moléculaire est appliquée à des substances formées d'atomes magnétiquement identiques les uns aux autres. Dans sa notion de champ moléculaire local, Néel a donc rendu compte de la différence entre des atomes magnétiques dans un même matériau.

Avec sa théorie, Weiss émet deux hypothèses :

• Un moment magnétique atomique est soumis à un champ résultant de la somme du champ appliqué ${\displaystyle H_{0}}$ et du champ des autres moments magnétiques, appelé champ moléculaire ${\displaystyle H_{m}}$^[2] :

${\displaystyle H=H_{0}+H_{m}}$ ;

• Ce champ moléculaire est proportionnel à l’aimantation locale ${\displaystyle M}$ :

${\displaystyle H_{m}=\alpha \times M}$,

où ${\displaystyle \alpha }$, appelé coefficient du champ moléculaire, est une constante indépendante de la température et de l’aimantation.

Soit un système de spins en interaction soumis à un champ magnétique ${\displaystyle H_{0}}$, que l’on décrit à l’aide d’un hamiltonien d'Heisenberg-Dirac ^[3].

${\displaystyle H=\sum _{ij}J_{ij}.S_{i}.S_{j}-g_{i}.\mu _{B}.H_{0}.\sum _{i}S_{i}}$,

où ${\displaystyle S_{i}}$ et ${\displaystyle S_{j}}$ sont des opérateurs spin, ${\displaystyle \mu _{B}}$ est le magnéton de Bohr, ${\displaystyle g_{i}}$ est le rapport gyromagnétique du ${\displaystyle i}$-ème moment localisé.

Grâce à l’équation du mouvement du spin ${\displaystyle S_{i}}$ :

${\displaystyle i\hbar {\operatorname {d} \!S_{i} \over \operatorname {d} \!t}=[S_{i},H]}$,

on en déduit que :

${\displaystyle i\hbar {\operatorname {d} \!S_{i} \over \operatorname {d} \!t}=g_{i}.\mu _{B}.S_{i}\land (H_{0}+H_{i})}$,

où ${\displaystyle H_{i}={\frac {1}{g.\mu _{B}}}\sum _{ij}J_{ij}.S_{j}}$.

${\displaystyle H_{i}}$ dépend de l’espace et du temps car le spin varie, d’atome à atome.

On montre ainsi que le mouvement du spin ${\displaystyle S_{i}}$ est analogue au mouvement d’un moment magnétique dans un champ ${\displaystyle H_{i}}$ et que le champ moléculaire que l’on a défini grâce à un hamiltonien est une forme bilinéaire de spins.

La seconde hypothèse de Weiss peut être déduite grâce à une approximation statistique.

En effet, si on remplace ${\displaystyle H_{i}(r_{i},t)}$ par sa valeur moyenne, on obtient :

${\displaystyle H_{m}=<H_{i}(r_{i},t)>={\frac {1}{g_{i}.\mu _{B}}}\sum _{ij}J_{ij}.<S_{j}>}$,

où ${\displaystyle <S_{j}>={\frac {M}{N.g_{i}.\mu _{B}}}}$.

Si l’on ne considère maintenant que les interactions entre ${\displaystyle z}$ premiers voisins, on a alors :

${\displaystyle H_{m}=<H_{i}(r_{i},t)>={\frac {J.z}{g_{i}.\mu _{B}}}<S>={\frac {J.z}{N.g.\mu _{B}}}M}$.

De plus, on sait que l’énergie du moment magnétique ${\displaystyle \mu =g.\mu _{B}.S_{i}}$, soumis à un champ ${\displaystyle H_{0}+H_{i}}$

${\displaystyle E=-S_{i}.(H_{0}+H_{i})=-\sum _{i}J_{ij}.S_{i}.S_{j}-S_{i}.H_{0}}$.

Si l’on applique la théorie de Langevin en supposant que le spin ${\displaystyle S_{i}}$ est soumis à un champ magnétique ${\displaystyle H_{0}+<H_{i}>}$, on obtient alors :

${\displaystyle E=-J.z<S_{j}>.S_{i}-H_{0}.S_{i}}$.

On utilise ici le fait que, comme les particules en interaction sont indépendantes dans un champ moyen,

${\displaystyle <S_{i}.S_{j}>=<S_{j}.S_{i}>}$.

Si l’on suppose maintenant que chaque atome est en interaction directe avec tous les autres atomes du cristal, c’est-à-dire que ${\displaystyle z=N}$, on obtient :

${\displaystyle \sum _{ij}J_{ij}.S_{j}=J.N.<S>=J.M}$.

Ce qui traduit que le champ est indépendant de l'atome ${\displaystyle i}$ : la fluctuation du spin n'intervient plus dans l'expression.

La théorie du champ moléculaire sera d'autant meilleure que le nombre de voisins est grand, il n'est toutefois pas nécessaire de considérer tous les atomes car l'intégrale d'échange décroit très rapidement avec la distance. Le modèle s'adapte bien aux moyennes et hautes températures. Le remplacement des grandeurs par leurs valeurs moyennes rend le modèle inadapté à l'étude des matériaux à basse température. En effet, les excitations à basse température provoquent des fluctuations de l’aimantation d'un atome à l'autre qui ne sont pas négligeables. Lorsque la température monte, l'agitation thermique devient prépondérante devant ces corrélations et l'emploi de la valeur moyenne devient justifié.

Dans sa théorie sur le champ moléculaire, Weiss n’a considéré que des atomes équivalents. Néel a, quant à lui, étendu cette théorie aux substances qui contiennent plusieurs types d’atomes magnétiques. Il introduit ainsi un nouveau concept : le champ moléculaire local.

Si l’on considère un système de spins de deux types d’atomes en interaction ${\displaystyle a}$ (${\displaystyle i,j}$) et ${\displaystyle b}$ (${\displaystyle i',j'}$), soumis à un champ magnétique ${\displaystyle H_{0}}$, que l’on décrit à l’aide d’un hamiltonien d'Heisenberg, on obtient ^[4] :

${\displaystyle H=-\sum _{i,j}J_{i,j}.S_{i}.S_{j}-\sum _{i'j'}J_{i'j'}.S_{i'}.S_{j'}-\sum _{i,i'}J_{ii'}.S_{i}.S_{i'}-H_{0}\sum _{i}S_{i}-H_{0}\sum _{i'}S_{i'}}$.

Ainsi, le spin ${\displaystyle S_{i}}$ est soumis à un champ total ${\displaystyle H_{0}+H_{ai}}$ tel que :

${\displaystyle H_{ai}=\sum _{j}J_{ij}.S_{j}+\sum _{i'}J_{ii'}.S_{i'}}$.

De façon analogue pour le spin ${\displaystyle S_{i'}}$.

Si l’on remplace maintenant ${\displaystyle H_{ai}}$ et ${\displaystyle H_{bi'}}$ par leurs valeurs moyennes en utilisant le fait que :

${\displaystyle S_{a}=<S_{i}>}$ et ${\displaystyle S_{b}=<S_{i'}>}$,

on obtient deux champs moléculaires, un premier qui agit sur les atomes ${\displaystyle a}$ et un second qui agit sur les atomes ${\displaystyle b}$ :

${\displaystyle H_{a}=W_{aa}.S_{a}+W_{ab}.S_{b}}$,

${\displaystyle H_{b}=W_{ba}.S_{a}+W_{bb}.S_{b}}$,

où ${\displaystyle W}$ est une constante indépendante de la température.

On peut ainsi déterminer l’énergie de ce système :

${\displaystyle E=-{\frac {1}{2}}.W_{aa}.(N.S_{a})^{2}-{\frac {1}{2}}.W_{bb}.(N.S_{b})^{2}-{\frac {1}{2}}.W_{ab}.N^{2}.S_{a}.S_{b}}$.

C’est en minimisant l’expression de cette énergie que Néel a découvert de manière théorique le ferrimagnétisme et l’antiferromagnétisme. Ainsi, la théorie du champ moléculaire local apparaît comme une généralisation du champ moléculaire de Weiss qui décrit uniquement les matériaux ferromagnétiques.

Par ses travaux, Weiss a considérablement contribué à la théorie classique du ferromagnétisme. Son modèle s’inspire de la théorie de Langevin qui rendait compte du comportement des corps diamagnétiques et paramagnétiques. Modélisation de Weiss : ${\displaystyle H_{m}=W.M}$ ; modélisation de Langevin ${\displaystyle L(M)=\coth(M)-{1 \over M}}$ .

La théorie de ferromagnétisme de Weiss repose sur les principes suivants^[5] :

• Chaque molécule éprouve de la part de l’ensemble des molécules environnantes une action égale à celle d’un champ uniforme, proportionnel à leur orientation et de même direction. On appelle ce dernier le champ moléculaire.
• Dans un corps ferromagnétique, de la même manière que dans un liquide, il n’y a pas d'énergie potentielle qui dérive de la rotation des molécules. Le champ moléculaire ne dépend ainsi que de l’interaction des molécules les unes avec les autres.

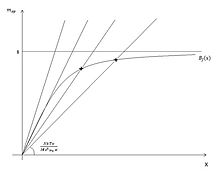
Il donne donc l’équation suivante régissant le comportement de l’intensité d’aimantation :

${\displaystyle M={\frac {a.\gamma .T}{\mu .N}}}$,

où ${\displaystyle a}$ est une constante proportionnelle, au champ moléculaire et au champ exigé par la formule de Langevin, ${\displaystyle \mu }$ le moment magnétique d'une molécule, ${\displaystyle \gamma .T}$ deux fois la force vive d'un degré de liberté de la molécule, ${\displaystyle N.M}$ un champ uniforme proportionnel à l'intensité d'aimantation et de même direction.

L'intensité de facile aimantation doit donc respecter les résultats obtenus par Weiss, mais également les modélisations de Langevin. Elle peut donc être obtenue graphiquement par l'intersection des deux courbes.

Il apparaît donc que plus la température augmente, plus la pente de la droite affine augmente. Au delà d’une température que Weiss a identifié comme la température de Curie, le matériau adopte un comportement paramagnétique.  

En appliquant la méthode du champ moléculaire local, Néel s’est intéressé aux substances ne contenant qu'une seule sorte d'ions magnétiques, mais en considérant un coefficient d'échange négatif. Il s’est aperçu qu’à basse température, des sous-réseaux pouvaient présenter un ordre magnétique mais avec des aimantations anti-parallèles, de sorte que l'aimantation spontanée macroscopique soit nulle. On obtient alors un comportement similaire à un matériau antiferromagnétique : la susceptibilité est indépendante de la température et est quasiment nulle.

Au-dessus d’une certaine température de transition antiferromagnétique, usuellement appelée température de Néel, la susceptibilité obéit à la loi de Curie-Weiss ^[6] :

${\displaystyle \chi ={\frac {C}{T+\Theta }}}$,

et le matériau se comporte alors comme un matériau paramagnétique.

La théorie des matériaux ferrimagnétiques, née plus de dix ans après celle de l'antiferromagnétisme, s'appuie directement sur le champ moléculaire local ^[4]. Ces matériaux possèdent une aimantation spontanée dans lesquels les moments magnétiques sont anti-parallèles, mais d'intensités différentes, ce qui résulte en une aimantation non-nulle.

Cette propriété est dépendante de la température :

• A basse température : deux sous réseaux, l’un que l’on nommera le sous réseau A et l’autre le sous réseau B qui sont tous deux aimantés. L’aimantation résultante est la différence des deux, inférieure à la somme des moments des ions.

• A haute température (au-delà de la température de Curie) : région paramagnétique, c’est-à-dire que pour que le matériau soit à nouveau aimanté, il va falloir appliquer un champ magnétique extérieur.

• Température de compensation : température à laquelle l’aimantation du sous réseau A est égale à l’aimantation du sous réseau B, impliquant donc une aimantation macroscopique nulle.

L'hélimagnétisme résulte d'une compétition, à l'intérieur d'un même matériau, entre les interactions d'échanges ferromagnétique et antiferromagnétique

Dans ce type de matériaux, les moments magnétiques voisins sont disposés selon un motif en hélice, mais on peut considérer qu'ils sont disposés en feuillets. Au sein d’un plan du feuillet, tous les atomes ont leurs spins parallèles.

Soit ${\displaystyle \phi }$ l’angle que font deux spins atomiques de deux feuillets voisins.

On peut ainsi définir le spin d’un atome en position ${\displaystyle R_{i}}$ comme ^[7] :

${\displaystyle <S_{i}>=\eta .e^{ik_{0}.R_{i}}}$,

où ${\displaystyle k_{0}}$est tel que ${\displaystyle \phi =k_{0}.d}$, avec ${\displaystyle d}$ la distance entre deux feuillets.

Soit ${\displaystyle H_{i}}$ le champ moléculaire agissant sur un atome ${\displaystyle i}$ :

${\displaystyle H_{i}=\sum _{j}J_{ij}.<S_{j}>=\eta .\sum _{j}J_{ij}.e^{ik_{0}.R_{j}}=\eta .e^{ik_{0}.R_{i}}\sum _{j}J_{ij}.e^{ik_{0}.(R_{j}-R_{i})}=H_{0}.e^{ik_{0}.R_{i}}}$,

où ${\displaystyle H_{0}}$, fonction de ${\displaystyle k_{0}}$, est proportionnelle à la transformée de Fourier de l’intégrale d’échange.

Cet état magnétique est souvent observé à basse température et est courant pour les terres rares.

Au niveau macroscopique, l'aimantation totale d'un système hélimagnétique est nulle ou très faible, car les moments sont orientés dans toutes les directions du plan.

• Pierre Weiss
• Louis Néel
• Loi de Curie
• Hélimagnétisme
• Ferrimagnétisme
• Ferromagnétisme
• Antiferromagnétisme
• Critère de Ginzburg

• A.Herpin, Le champ moléculaire. Journal de Physique Colloques, 1971, 32 (C1), pp.C1-4-C1-10. HAL, Archives ouvertes.
• Pierre Weiss, L'hypothèse du champ moléculaire et la propriété ferromagnétique, Journal de physique théorique et appliquée, J. Phys. Theor. Appl., 6 1 (1907) 661-690. HAL, Archives ouvertes.
• Louis Néel, Le champ moléculaire de Weiss et le champ moléculaire local, Colloque National de Magnétisme, Édition du CNRS, Juillet 1957. Lien
• Florent Calvayrac, Milieux diélectriques et magnétiques, Cours en ligne de l'Université du Maine, Le Mans - Laval, 2011 Lien
• Steven H. Simon, Lecture Notes for Solid State Physics, Support de cours du département de Physique de l'Université d'Oxford, Janvier 2012. Lien

• Portail de la physique