Triangle de Reuleaux — Wikipédia

Un triangle de Reuleaux est une courbe de largeur constante, c'est-à-dire une courbe dont tous les diamètres ont la même longueur. Dans ce cas un diamètre correspond au segment formé par un sommet et n'importe quel point du côté opposé (qui est un arc de cercle dans ce cas). Cette courbe tient son nom de l'ingénieur allemand Franz Reuleaux, qui fut au XIX^e siècle un pionnier du génie mécanique.

La forme du triangle de Reuleaux a été utilisée au treizième siècle pour certaines rosaces gothiques.

Plus tard, on peut voir la construction de ce triangle dans plusieurs manuscrits de Léonard de Vinci. Toutefois, rien ne montre que Léonard ait suspecté les propriétés de roulante de cette figure.

Leonhard Euler a étudié ces formes qu’il nommait « orbiforme^[1] ».

Reuleaux est le premier à avoir caractérisé cette courbe comme une courbe de largeur constante et suspecté les applications cinématiques de cette figure^[2].

• 
  Fenêtre de la façade principale éclairant le collatéral, Cathédrale Notre-Dame d'Amiens.
• 
  Fenêtre en forme de triangle de Reuleaux, Cathédrale Saint-Sauveur de Bruges.
• 
  Fenêtres hautes en forme de triangles de Reuleaux dans la nef de la Cathédrale de Lichfield.
• 
  « Triangle de Reuleaux » sur un manuscrit de Léonard de Vinci.

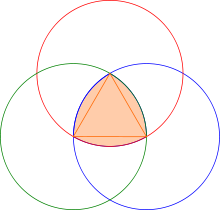
Pour construire un triangle de Reuleaux, on part d'un triangle équilatéral. Depuis chaque sommet pris tour à tour, on décrit un arc de cercle entre les deux autres sommets. Les trois arcs raccordés forment un triangle de Reuleaux.

On peut généraliser la construction de Reuleaux aux polygones ayant un nombre de côtés impair : on obtient ainsi des polygones curvilignes de largeur constante, les polygones de Reuleaux. Ces polygones peuvent même être irréguliers.

On observe facilement que le périmètre P d'un triangle de Reuleaux de rayon des arcs r est égal à la moitié de celui d'un cercle de rayon r (car la courbe est formée de trois arcs de cercle de rayon r et d'angle ^π⁄₃).

${\displaystyle {\mathcal {P}}=\pi r}$

L’aire A de ce même triangle est : ${\displaystyle {\mathcal {A}}={\frac {1}{2}}(\pi -{\sqrt {3}})\times r^{2}.}$ On peut le montrer en remarquant que l'aire est celle de secteurs angulaires d'angle ^π⁄₃ et de rayon r, à laquelle on soustrait deux fois l'aire d'un triangle équilatéral de côté r.

Un théorème dû à Wilhelm Blaschke et Henri-Léon Lebesgue établit que cette courbe possède, parmi les courbes d'égale largeur, une surface minimale.

Comme tous les diamètres ont même longueur, un polygone de Reuleaux répond à la question suivante : « Quelle forme doit avoir une plaque d'égout pour ne pas tomber dans le regard de visite ? » La réponse la plus simple est le cercle, mais le triangle de Reuleaux convient également. La ville de San Francisco par exemple utilise également des triangles de Reuleaux^[3].

La came de Reuleaux est souvent utilisée en mécanique, comme dans l'animation ci-contre à droite du deuxième modèle de Cinématographe des Frères Lumière (la came de Reuleaux ou triangle de Reuleaux y remplaçait la came excentrique d'origine).

On associe le triangle de Reuleaux au compresseur rotatif du moteur Wankel. Le rotor de ce moteur est effectivement à la base un triangle de Reuleaux, dont les faces sont creusées pour augmenter le volume de la chambre de combustion.

Une autre application particulièrement remarquable de ces triangles est l'existence de mèches pour foreuses qui percent des trous « carrés » ou presque^[4].

Au Royaume-Uni, les pièces de 20 et 50 pence sont des heptagones de Reuleaux en cupronickel.

L'horloger britannique Derek Pratt (1938–2009) en a fait une utilisation remarquable dans l'un de ces mouvements mécaniques dans le but d'y intégrer une vieille complication horlogère : la seconde morte.

L'intersection de sphères de rayon commun s, et dont les centres sont au sommet d'un tétraèdre de côté s s'appelle tétraèdre de Reuleaux.

Contrairement à l'intuition, le tétraèdre de Reuleaux n'est pas de largeur constante : le diamètre de ce solide, qui est la distance entre deux points situés au milieu de deux arêtes opposées, est supérieur à la distance séparant deux sommets : ${\displaystyle {\frac {d}{s}}={\sqrt {3}}-{{\sqrt {2}} \over 2}\approx 1{,}0249}$

• (en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « Reuleaux triangle » (voir la liste des auteurs).

• Explications et animations en français
• (en) Eric W. Weisstein, « Reuleaux Triangle », sur MathWorld
• (de) Reuleaux-Dreieck in Fahrt (Le triangle de Reuleaux en action)
• (ru) « Круглый треугольник Рело », sur You Tube (Film sur les applications du triangle de Reuleaux)

• Portail de la géométrie