Bástyagráf – Wikipédia

Bástyagráf
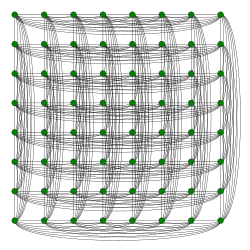8×8-as bástyagráf
Csúcsok száma	nm
Élek száma	nm(n + m)/2 − nm
Átmérő	2
Derékbőség	3 (ha max(n, m) ≥ 3)
Kromatikus szám	max(n, m)
Egyéb	reguláris, csúcstranzitív, perfekt jól fedett

A matematika, azon belül a gráfelmélet területén egy bástyagráf (rook's graph) olyan gráf, ami a sakkjátékban szereplő bástya nevű figura lehetséges lépéseit jeleníti meg egy sakktáblán: a csúcsok a sakktábla egy-egy mezőjét jelképezik, az élek pedig a legális lépéseket köztük. A bástyagráfok erősen szimmetrikus, perfekt gráfok; jellemző rájuk, hogy éleik hány háromszöghöz tartoznak, valamint a nem szomszédos csúcspárokat összekötő 4-körök létezése. A bástyagráf a sakkfigurák gráfjai között (futógráf, huszárgráf, királygráf, vezérgráf) egyedülálló szimmetriákat és regularitást mutat.

Egy n × m-es bástyagráf a bástya lépési lehetőségeit mutatja meg egy n × m-es sakktáblán. Csúcsaihoz (x, y) koordináták rendelhetők, ahol 1 ≤ x ≤ n és 1 ≤ y ≤ m egész számok. Az (x₁, y₁), illetve (x₂,y₂) csúcsok pontosan akkor szomszédosak, ha az x₁ = x₂ és az y₁ = y₂ állítások valamelyike igaz; tehát ha a sakktábla azonos oszlopában vagy sorában találhatóak.

Egy n × m-es bástyagráfnál a csúcsok száma nm, az n × n-es bástyagráfnál (amilyen a normál sakktábla is, n=8), a csúcsok száma n², az élek száma pedig n³ − n²; ebben az esetben a gráf egy kétdimenziós Hamming-gráf vagy latin négyzet-gráf.

Minden bástyagráf 2-összefüggő és rendelkezik Hamilton-körrel az elfajult n=1 vagy m=1 eset kivételével. A bástyagráf speciális esete az 1×n-es sakktáblán a ${\displaystyle K_{n}}$ teljes gráf.

Egy n × m-es bástyagráf meghatározható úgy is, mint a K_n és K_m teljes gráfok Descartes-szorzata, képlettel kifejezve K_n ◻ K_m. A 2 × n-es bástyagráf komplementere egy koronagráf.

(Moon 1963) és (Hoffman 1964) jellemzése alapján az m × n-es bástyagráfok a következő egyedi, rájuk jellemző tulajdonságokkal bírnak:^[1][2]

• mn csúccsal rendelkezik, melyek mindegyikéhez n + m − 2 él tartozik.
• Az élek közül pontosan mn(m − 1)/2 tartozik m − 2 háromszöghöz, a maradék mn(n − 1)/2 él pedig n − 2 háromszöghöz (a háromszögelés során a bástya megtartja vagy saját sorát, vagy saját oszlopát).
• Bármely két, nem szomszédos csúcs pontosan egy, rájuk jellemző 4-körhöz tartozik.

Ha n = m, a feltételek rövidebben úgy is megfogalmazhatók, hogy az n × n-es bástyagráf erősen reguláris gráf srg(n², 2n − 2, n − 2, 2) paraméterekkel, és minden ezekkel a paraméterekkel rendelkező, erősen reguláris gráf egy n × n-es bástyagráf, kivéve, ha n ≠ 4. Az n = 4 esetben létezik még egy, az 4 × 4 bástyagráf paramétereivel megegyező erősen reguláris gráf, méghozzá a Shrikhande-gráf. A Shrikhande-gráf és a 4 × 4-bástyagráf könnyen megkülönböztethetők egymástól, mivel a bástyagráf bármely csúcsának szomszédságában két háromszög, a Shrikhande-gráf bármely csúcsának szomszédságában pedig egy 6-kör található.

A bástyagráfok csúcstranzitív és (n + m − 2)-reguláris gráfok; ők az egyetlen, standard sakkfigurák mozgását leíró reguláris gráfok.^[3] Ha m ≠ n, a bástyagráf szimmetriái a gráf sorainak, illetve oszlopainak külön-külön permutálásából adódnak. Ha n = m, a gráf további, a sorok és oszlopok felcseréléséből adódó szimmetriákkal is rendelkezik.

A bástyagráf bármely két csúcsa vagy 1 vagy 2 távolságra van egymástól. Bármely két, nem szomszédos csúcs transzformálható másik két nem szomszédos csúccsá a gráf egy szimmetriája segítségével. Ha a bástyagráf nem négyzetes, a szomszédos csúcspárok a szimmetriacsoport két pályájába esnek, attól függően, hogy vízszintesen vagy függőlegesen szomszédosak; ha viszont a gráf négyzetes, bármely két szomszédos csúcs átvihető egymásba egy szimmetria segítségével, ezáltal a gráf távolságtranzitív.

Ha m és n relatív prímek, a bástyagráf S_m × S_n szimmetriacsoportja alcsoportként magában foglalja a C_mn = C_m × C_n ciklikus csoportot, ami az mn csúcs ciklikus permutációjával hat; ebben az esetben tehát a bástyagráf egy cirkuláns gráf.

A bástyagráf úgy is tekinthető, mint a K_n,m teljes páros gráf élgráfja – tehát olyan gráf, ami a K_n,m minden éléhez egy csúcsot tartalmaz, és két csúcsa akkor szomszédosak, ha a teljes páros gráfban a megfelelő élek közös végpontból indulnak.^[4] Így tekintve, a teljes páros gráf egy éle, ami a bipartíció egyik oldalának i-edik csúcsa és a bipartíció másik oldalának j-edik csúcsa között húzódik, egy sakktábla (i, j) koordinátájú mezőjének felel meg.

Bármely páros gráf egy teljes páros gráf részgráfja, ennek megfelelően bármely páros gráf élgráfja egy bástyagráf feszített részgráfja.^[5] A páros gráfok élgráfjai perfektek: bennük, és bármely feszített részgráfjukban a színezésükhöz szükséges színek száma megegyezik legnagyobb teljes részgráfjuk (klikkjük) csúcsainak számával. A páros gráfok élgráfjai a perfekt gráfok fontos családját alkotják: egyikét alkotják a (Chudnovsky et al. 2006) által a perfekt gráfok karakterizációjához felhasznált kevés számú családnak, melyekkel megmutatták, hogy a páratlan lyukak és páratlan antilyukak nélküli gráfok perfektek.^[6] Továbbá a bástyagráfok maguk is perfektek.

Mivel a bástyagráfok perfektek, a gráf színezéséhez annyi színre van szükség, mint a legnagyobb klikkjének a mérete. A bástyagráfok klikkjei sorainak és oszlopainak részhalmazai, ezek közül a legnagyobbaknak a mérete max(m, n), tehát ennyi a gráf kromatikus száma is. Egy n × n-es bástyagráf n-színezése latin négyzetként is értelmezhető: leírja, hogy lehet az n × n-es rács sorait és oszlopait úgy feltölteni n különböző értékkel, hogy ugyanaz az érték ne jelenjen meg egynél többször ugyanabban a sorban vagy oszlopban.^[7]

Nyolc, egymást nem támadó bástya a sakktáblán; a megfelelő bástyagráfban ezek maximális elemszámú független csúcshalmazt alkotnak

Egy bástyagráf független csúcshalmaza olyan csúcsok halmaza, melyek közül semelyik sincs a gráf azonos oszlopában vagy sorában, azaz, sakk-terminológiával élve olyan, a sakktáblán elhelyezett bástyákról van szó, melyek közül semelyik sem áll ütésben a többiek által. A perfekt gráfok úgy is leírhatók, mint olyan gráfok, melyek minden feszített részgráfjában a legnagyobb független csúcshalmaz mérete megegyezik a lehető legkevesebb klikkbe particionálásban a klikkek számával. Egy bástyagráfban a sorok halmaza vagy az oszlopok halmaza (amelyik kisebb) ilyen optimális partíciót alkot. A gráf legnagyobb független csúcshalmazának mérete ezért min(m, n). A bástyagráf bármely optimális színezésének összes színosztálya maximális elemszámú független csúcshalmazt alkot.

Egy gráf dominálási száma a legkisebb domináló halmazának elemszámával egyezik meg. A bástyagráfban egy csúcshalmaz pontosan akkor domináló halmaz, ha az m × n-es sakktáblán nekik megfelelő mezők vagy megegyeznek, vagy egy bástyalépés távolságra vannak a többi mezőtől. Az m × n-es táblán a dominálási szám min(m, n).^[8]

A bástyagráf egy k-domináló halmaza olyan csúcshalmaz, melyhez tartozó mezőkön álló bástyák minden más mezőt legalább k-szor támadnak. A bástyagráf k-tuple domináló halmaza olyan csúcshalmaz, melyhez tartozó mezőkön álló bástyák minden más mezőt legalább k-szor támadnak, és ők maguk is legalább k − 1-szer ütésben állnak. Ak-domináló és k-tuple domináló halmazok közül a legkisebb számosságúnak az elemszámát k-dominációs számnak, illetve k-tuple dominációs számnak nevezik. Négyzetes táblán, páros k-ra a k-dominációs szám nk/2, ha n ≥ (k² − 2k)/4 és k < 2n. Hasonlóan, a k-tuple dominációs szám n(k + 1)/2, ha k páratlan és kisebb, mint 2n.^[9]

• Futógráf
• Huszárgráf
• Királygráf
• Vezérgráf
• Rácsgráf

• Weisstein, Eric W.: Lattice Graph (angol nyelven). Wolfram MathWorld