ファイル:Lavaurs-12.png

このプレビューのサイズ: 600 × 600 ピクセル。 その他の解像度: 240 × 240 ピクセル | 480 × 480 ピクセル | 768 × 768 ピクセル | 1,024 × 1,024 ピクセル | 2,000 × 2,000 ピクセル。
元のファイル (2,000 × 2,000 ピクセル、ファイルサイズ: 356キロバイト、MIME タイプ: image/png)
ウィキメディア・コモンズのファイルページにある説明を、以下に表示します。 |
概要
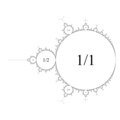
| 解説Lavaurs-12.png | English: Topological model of Mandelbrot set using Lavaurs algorithm up to period 12. " The quadratic minor lamination, or QML, is defined by Thurston to be the union of S 1 with all minor leaves. ... The QML is conjecturally equivalent to the Mandelbrot set; this conjecture being equivalent to that stating that the Mandelbrot set is locally connected." [1] Français : modèle topologique de l'ensemble de Mandelbrot, utilisant l'algorithme de Lavaurs jusqu'à la période 12 Polski: Topologiczny model zbioru Mandelbrota dla okresów 1-12. Korzysta z algorytmu Lavaurs'a. |
| 日付 | |
| 原典 | own code based on the Lisp code by R Berenguel |
| 作者 | Adam majewski |
compare with
- quadratic invariant lamination
associated with rabbit Julia set
- quadratic invariant lamination
associated with basilica Julia set
- Shrub model
Programs :
ライセンス
この作品の著作権者である私は、この作品を以下のライセンスで提供します。
このファイルはクリエイティブ・コモンズ 表示-継承 3.0 非移植ライセンスのもとに利用を許諾されています。
- あなたは以下の条件に従う場合に限り、自由に
- 共有 – 本作品を複製、頒布、展示、実演できます。
- 再構成 – 二次的著作物を作成できます。
- あなたの従うべき条件は以下の通りです。
- 表示 – あなたは適切なクレジットを表示し、ライセンスへのリンクを提供し、変更があったらその旨を示さなければなりません。これらは合理的であればどのような方法で行っても構いませんが、許諾者があなたやあなたの利用行為を支持していると示唆するような方法は除きます。
- 継承 – もしあなたがこの作品をリミックスしたり、改変したり、加工した場合には、あなたはあなたの貢献部分を元の作品とこれと同一または互換性があるライセンスの下に頒布しなければなりません。
 | この文書は、フリーソフトウェア財団発行のGNUフリー文書利用許諾書 (GNU Free Documentation License) 1.2またはそれ以降のバージョンの規約に基づき、複製や再配布、改変が許可されます。不可変更部分、表紙、背表紙はありません。このライセンスの複製は、GNUフリー文書利用許諾書という章に含まれています。http://www.gnu.org/copyleft/fdl.htmlGFDLGNU Free Documentation Licensetruetrue |
あなたは上記のライセンスから、どれか一つ以上を選択できます。
Src code
; console program ; Lisp / Common Lisp / SBCL ; based on : ; http://www.mostlymaths.net/2009/08/lavaurs-algorithm.html ; lisp code by R Berenguel ; reducible angle is not angle of lower period ; for example 9/15 = 3/5 has period 4 ; ; Rules by Lavaures : ; no arc crosses any other arc ; arc connects 2 angles with the same period : first and second ; first angle is the smallest angles not yet connected, and second angle is the next smallest angle not yet connected ; ; orthogonal circles (x1,y1,r1) and (x2,y2,r2) ; r1^2 + r2^2 = (x2-x1)^2 +(y2-y1)^2 ; http://planetmath.org/encyclopedia/OrthogonalCircle.html ; http://classes.yale.edu/fractals/Labs/NonLinTessLab/BasicConstr3.html ; ; example of use : ; ; sbcl ; (load "ls.lisp") ; (draw-lavaurs "lavaurs-5.png" 2000 5) ; ;look for lavaurs-5.png file in your home directory ; ; Adam Majewski ; fraktal.republika.pl ; 2010.09.04- 11.17 ; ; ;; This program is free software: you can redistribute it and/or ;; modify it under the terms of the GNU General Public License as ;; published by the Free Software Foundation, either version 3 of the ;; License, or (at your option) any later version. ;; This program is distributed in the hope that it will be useful, ;; but WITHOUT ANY WARRANTY; without even the implied warranty of ;; MERCHANTABILITY or FITNESS FOR A PARTICULAR PURPOSE. See the GNU ;; General Public License for more details. ;; You should have received a copy of the GNU General Public License ;; along with this program. If not, see ;; <http://www.gnu.org/licenses/>. ; first run ;(require :asdf) ;(require :asdf-install) ;(asdf-install:install :zpng) ;(asdf-install:install :Vecto) ; http://www.xach.com/lisp/vecto/ ; you must press 2 and 0 when the program asks ; next times load packages from disk (asdf:operate 'asdf:load-op 'vecto) (defun doubling-map (ratio-angle) " period doubling map = The dyadic transformation (also known as the dyadic map, bit shift map, 2x mod 1 map, Bernoulli map, doubling map or sawtooth map " (let* ((n (numerator ratio-angle)) (d (denominator ratio-angle))) (setq n (mod (* n 2) d)) ; (2 x n) modulo d = doubling (/ n d))) (defun give-period (ratio-angle) "gives period of angle in turns (ratio) under doubling map" (let* ((n (numerator ratio-angle)) (d (denominator ratio-angle)) (temp n)) ; temporary numerator (loop for p from 1 to 100 do (setq temp (mod (* temp 2) d)) ; (2 x n) modulo d = doubling) when ( or (= temp n) (= temp 0)) return p ))) (defun give-list (period) "Returns a list of all angles of given period without angles with lower periods, which divide period. period is integer > 0 " (let* ((angles-list '()) (den (- (expt 2 period) 1 )) ; denominator of angle = (2^period)-1 a ) ; angle (when (> period 0) (dotimes (num (+ den 1)) ; from 0 to den (setq a (/ num den )) (when (= period (give-period a)) ; (setq angles-list (append angles-list (list a)))))) ; angles-list)) (defun not-crosses (new-pair old-pair) "checks if new arc ( = between new-angle-1 and new-angle-2) crosses old arc ( = between (first old-pair) and (second old-pair)). It is a part of Lavaurs algorithm. Angles are external angles mesured in turns angle-1 < angle-2 test : (setq old-p '(1/3 2/3)) (setq new-p '(4/15 6/15)) (not-crosses new-p old-p) (not-crosses (list 1/7 2/7) old-p) ; t (not-crosses (list 1/7 3/7) old-p) ; nil " (let ((old-angle-1 (first old-pair)) (old-angle-2 (second old-pair)) (new-angle-1 (first new-pair)) (new-angle-2 (second new-pair))) ; check the order of input angles (when (< new-angle-2 new-angle-1) (rotatef new-angle-1 new-angle-2)) (when (< old-angle-2 old-angle-1) (rotatef old-angle-1 old-angle-2)) (cond ((< new-angle-1 new-angle-2 old-angle-1 old-angle-2) t) ((< old-angle-1 old-angle-2 new-angle-1 new-angle-2) t) ((< new-angle-1 old-angle-1 old-angle-2 new-angle-2) t) ((< old-angle-1 new-angle-1 new-angle-2 old-angle-2) t) (t nil)))) (defun not-crosses-all (new-pair old-list) "checks if new pair of rays do not crosses any of pairs from old list test : (setq old-pairs '((1/3 2/3) (1/7 2/7))) (not-crosses-all (list 4/15 6/15) old-pairs) ; nil " (let ((b-result T)) (loop for old-pair in old-list do (setq b-result (and b-result (not-crosses new-pair old-pair)))) b-result )) (defun give-pairs-up-to (period) "gives list of external angles (pairs landing on the same root point) for periods up to input period period >= 3 examples of use : (give-pairs-old-old 3) (give-pairs-old-old 7) " (let* ((pairs (list (list 1/3 2/3))) ; list for period 2 angles-list ; temporary list i new-first-angle new-second-angle) ( loop for p from 3 to period do (setq angles-list (give-list p)) (loop for j from 0 to (/ (- (length angles-list) 1) 2) do (setq new-first-angle (pop angles-list)) ; pop removes angle from list ; find second ( conjugate) angle (setq i 0) (loop do ;for i from 0 to (- (length angles-list) 1) do ; first = nth 0 (setq new-second-angle (nth i angles-list)) ; nth do not removes angle from list (setq i (+ i 1)) until (not-crosses-all (list new-first-angle new-second-angle) pairs)) (setq angles-list (remove new-second-angle angles-list)) (push (list new-first-angle new-second-angle) pairs))) ; save new pair to pairs list (reverse pairs))) ; it should be the same as number of components ;(loop for p from 3 to 10 do (print (length (give-pairs p)))) ;3 ;6 ;15 ;27 ;63 ;120 ;252 ;495 ; (defun give-pairs (period-max) "gives list of external angles (pairs landing on the same root point) for period = pariod-max period >= 2 examples of use : (give-pairs 3) (give-pairs 7) ; (time (give-pairs 16)) (compile 'give-pairs) " (let* ((pairs (list (list 1/3 2/3))) ; list for period 2 angles-list ; temporary list (previous-list pairs) ; list for "previous period" = (period -1) i new-first-angle new-second-angle) ( loop for period from 3 to period-max do (setq angles-list (give-list period)) ; find all angles for given period (setq previous-list pairs) ; update previous list ; match pairs of angles (loop for j from 0 to (/ (- (length angles-list) 1) 2) do (setq new-first-angle (pop angles-list)) ; pop removes angle from list ; find second ( conjugate) angle (setq i 0) (loop do ;for i from 0 to (- (length angles-list) 1) do ; first = nth 0 (setq new-second-angle (nth i angles-list)) ; nth do not removes angle from list (setq i (+ i 1)) until (not-crosses-all (list new-first-angle new-second-angle) pairs)) (setq angles-list (remove new-second-angle angles-list)) (push (list new-first-angle new-second-angle) pairs))); save new pair to pairs list (setq pairs (set-difference pairs previous-list :test 'equal)) ; remove previous angles (reverse pairs))) ; -------------------------------------- drawing code ------------------------------------------------ (defun ttr (turn) " Turns to Radians" (* turn (* 2 pi) )) ; circle-list angle-list (defun give-arc-list (circle-list angle-list) " Copyright 2009 Rubén Berenguel ruben /at/ maia /dot/ ub /dot/ es Find the ortogonal circle to the main circle, given the angles in it. Input : R: radius of the main circle angle1, angle2 : angles of main circles (in turns) (a, b) , (ba, bb) : points of main circle and new ortogonal circle Output is a list for vecto:arc procedure thru draw-arc procedure http://classes.yale.edu/fractals/Labs/NonLinTessLab/BasicConstr3.html " (let* ((x0 (first circle-list)) (y0 (second circle-list)) (r0 (third circle-list)) (alpha (ttr ( first angle-list))) ; convert units from turns to radians (balpha (ttr (second angle-list))) (gamma (+ alpha (/ (- balpha alpha) 2))) ; angle between alpha and balpha (ca (cos alpha)) (cg (cos gamma)) (sa (sin alpha)) (sg (sin gamma)) (temp (/ r0 (+ (* ca cg) (* sa sg)))) ; first common point (a (+ x0 (* r0 ca))) ; a = x0 + r0 * cos(alpha) (b (+ y0 (* r0 sa))) ; b = y0 + r0 * sin(alpha) ; center of ortogonal circle (x (+ x0 (* temp cg))) (y (+ y0 (* temp sg))) ; center of middle circle (xma (- x a)) (ymb (- y b)) ; radius of ortogonal circle (r (sqrt (+ (* xma xma) (* ymb ymb)))) ; angle of point (a,b) measured in new circle units (phi (atan r0 r))) ; result (list x y r (+ pi gamma phi) ; new balpha (- (+ pi gamma) phi) ; new alpha a b))) ; point (a,b) (defun draw-arc (circle-list angle-list) " computes otogonal circle using give-arc-list and draws arc using vecto:arcn procedure vecto:arcn x y radius angle1 angle2 " (let* ((arc-list (give-arc-list circle-list angle-list))) (vecto:move-to ( sixth arc-list) (seventh arc-list)) ; beginning of arc is point (a,b) (vecto:arcn ( first arc-list) ; x (second arc-list) ; y (third arc-list) ; radius (fourth arc-list) ; angle1 (fifth arc-list))) ; angle2 (vecto:stroke)) (defun draw-arcs (circle-list angles-list) "draws arc from angles-list using draw-arc procedure" (loop for angles in angles-list do (draw-arc circle-list angles))) ; example of use : (draw-lavaurs "a.png" 800 2) (defun draw-lavaurs (file side period) "computes and draws Lavaurs model of Mandelbrot set. " (vecto:with-canvas (:width side :height side) ; vecto (vecto:set-rgb-stroke 0 0 0) ; vecto (vecto:set-line-width 1) ; vecto (let* ( (x0 (/ side 2)) (y0 x0) ; (r0 (- x0 50)) ; leave place for titles (main-circle-list (list x0 y0 r0)) arc-list) ; main circle (vecto:centered-circle-path x0 y0 r0 ) ; arcs ( chords) (setq arc-list (give-pairs-up-to period)) ; compute (draw-arcs main-circle-list arc-list) ; draw (vecto:stroke)) ; before save ( vecto procedure) (print (vecto:save-png file)))) ; save image ;----------global var ---------------------- (defparameter *period* 4 " maximal period. It is an integer >= 2 ") (defparameter *size* 800 " size of image in pixels. It is an integer >= 0 ") (defparameter *file-name* (make-pathname :name (concatenate 'string "lavaurs-" (write-to-string *period*)) :type "png") "name (or pathname) of png file ") ;======================= run ===================================================================== (draw-lavaurs *file-name* *size* *period*) References
キャプション
このファイルの内容を1行で記述してください
このファイルに描写されている項目
題材
ウィキデータ項目がない値
7 11 2010
ファイルの履歴
過去の版のファイルを表示するには、その版の日時をクリックしてください。
| 日付と時刻 | サムネイル | 寸法 | 利用者 | コメント | |
|---|---|---|---|---|---|
| 現在の版 | 2023年8月3日 (木) 17:58 |  | 2,000 × 2,000 (356キロバイト) | Obscure2020 | Optimized with OxiPNG and ZopfliPNG. |
| 2010年11月7日 (日) 12:15 |  | 2,000 × 2,000 (916キロバイト) | Soul windsurfer | {{Information |Description={{en|1=Topological model of Mandelbrot set using Lavaurs algorith up to period 12}} |Source={{own}} |Author=Adam majewski |Date=2010-11-07 |Permission= |other_versions= }} |
ファイルの使用状況
以下のページがこのファイルを使用しています:
グローバルなファイル使用状況
以下に挙げる他のウィキがこの画像を使っています:
- en.wikipedia.org での使用状況
- en.wikibooks.org での使用状況


 French
French Deutsch
Deutsch