底 (初等幾何学)

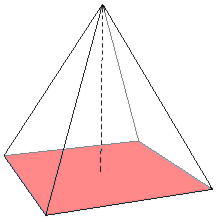
透過した四角柱の底面を脚色したもの。頭頂点 (apex) から頂垂線 (aplitude) が底面に垂直に降りている

初等幾何学における底（てい、英: base）は、図形の一番下（「底」（そこ）、"bottom"）と考えられる部分で、特に高さを測る方向に垂直な向きを持つ多角形の辺（底辺）や多面体の面（底面）を言う^[1]^{(pp38,315,353)}。よく用いられるのは、三角形、平行四辺形、台形などの底辺と、円柱、円錐、角錐、平行六面体、錐台などの底面である。

面積や体積の計算

底や高さは一般的な用例として図形の面積や体積の計算に利用される。この場合しばしば、底辺や底面の測度（長さや面積）のことを単に「底辺」や「底面」と呼ぶので注意が必要である。この語法を用いれば、平行四辺形の面積や角柱・円柱の体積は、その「底」掛ける「高さ」で計算できるということになる。同様に、三角形の面積や角錐・円錐の面積は、その底掛ける高さを適当な数値で割って得られる。台形や錐台のように、二つの平行な底を持つ図形が存在するが、図形の容積の計算にはどちらを用いても構わない^[2]。

三角形の底辺の延長線

三角形の辺の延長（英語版）の特別の場合として「底辺の延長線」(extended base) は底辺を含む直線を言う。鈍角三角形を考える上では底辺の延長は重要である。これは鋭角の頂点から引いた頂垂線 (三角形)が三角形の外部にあり、頂垂線は底辺とは交わらないが底辺の延長線とは垂直に交わることによる。