Gimbal lock – Wikipédia, a enciclopédia livre

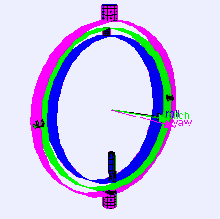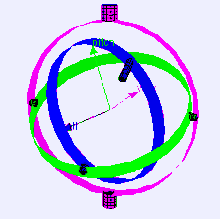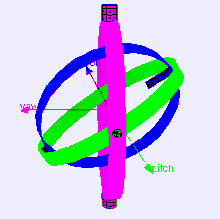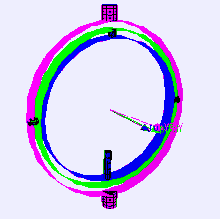
Gimbal lock (GL) é a perda de um grau de liberdade em um mecanismo tridimensional que ocorre quando os eixos de duas das suspensões cardãs (SC) são levadas a uma configuração paralela, "travando" o sistema de forma que só possa girar em um espaço bidimensional.

A palavra lock, que significa "trava" em inglês, é enganosa: a SC não está travada. Todas as três SCs ainda podem girar livremente em seus respectivos eixos de suspensão. No entanto, por causa da orientação paralela de dois dos eixos, não há SCs disponíveis para acomodar a rotação ao longo de um dos eixos.

Enquanto apenas duas orientações específicas produzem GL exata, na prática, mecanismos encontram dificuldades na vizinhança dessas orientações. Quando um conjunto de SC está perto da configuração travada, pequenas rotações da plataforma requerem grandes movimentos das SC mais externas. Embora a proporção seja infinita apenas no ponto de GL, na prática, os limites da velocidade e a aceleração das SC limitam o movimento da plataforma perto desse ponto.

GL pode ocorrer em sistemas de SC com dois graus de liberdade, como um teodolito com rotações em duas dimensões: azimute e elevação. Esses sistemas podem ter GL no zênite e nadir, porque nesses pontos o azimute não é bem definido, e rotações na direção do azimute não mudam a direção em que o teodolito está apontando.

Considere a possibilidade de monitorar um helicóptero voando do horizonte em direção ao teodolito. O teodolito é um telescópio montado sobre um tripé, de modo que ele pode mover-se em azimute e elevação para seguir o helicóptero. O helicóptero voa para o teodolito e é monitorado pelo telescópio em elevação e azimute. O helicóptero voa imediatamente acima do tripé (ou seja, ele está no zênite) quando ele muda de direção e voa em 90 graus em relação a seu curso anterior. O telescópio não pode monitorar essa manobra sem um salto descontínuo em uma ou ambas as orientações. Não há nenhum movimento contínuo que permita que ele siga o alvo. Essa é a GL. Assim, há uma infinidade de direções em torno de zênite em que o telescópio não pode monitorar continuamente todos os movimentos de um alvo.^[1] Note que mesmo que o helicóptero não passe pelo zênite, mas só perto do zênite, de modo que a GL não ocorra, o sistema ainda precisa mover-se excepcionalmente rápido para mantê-lo em vista, enquanto rapidamente passa de uma SC para outra. Quanto mais perto do zênite for o ponto, mais rápido isso deve ser feito, e se ele passa exatamente pelo zênite, estes movimentos "cada vez mais rápidos" tornam-se infinitamente rápidos, ou seja, descontínuos.

Para recuperar da GL o usuário tem que explicitamente dar uma volta em torno do zênite: reduzir a elevação, alterar o azimute para coincidir com o azimute de destino e, em seguida, alterar a elevação para que corresponda ao destino.

Matematicamente, isto corresponde ao fato de que as coordenadas esféricas não definem um atlas no zênite e no nadir da esfera. Isto é, o mapa correspondente T²→S² do toro T² para a esfera S² (dado pelo ponto dado com azimute e elevação) não é um recobrimento desses pontos.

Considere o caso de uma plataforma de sensor de nível em uma aeronave voando na direção norte, com seus três eixos mutuamente perpendiculares (ou seja, todos os ângulos roll - rolamento, pitch - inclinação e yaw - guinada iguais a zero). Se o pitch, que corresponde à elevação, virar 90 graus, o eixo de yaw da aeronave torna-se paralelo ao eixo de roll, e alterações em yaw não podem mais ser compensadas.

O problema pode ser resolvido com o uso de uma quarta SC, conduzida inteligentemente por um motor para que mantenha um ângulo grande entre as SC de roll e de yaw. Outra solução é girar uma ou mais SC para um ângulo arbitrário, removendo a trava.

A prática moderna é para evitar completamente o uso de SC. No contexto de sistemas de navegação por inércia, isso pode ser feito montando sensores inerciais diretamente no corpo do veículo (isso se chama sistema strapdown)^[2], integrando sensores de rotação e aceleração e digitalmente usando métodos de quaterniões para derivar a orientação e velocidade do veículo. Outra forma de substituir SC é a utilização de rolamentos fluidos ou de uma câmara de flotação.^[3]

Um incidente famoso com GL aconteceu na missão lunar Apolo 11. Nesta nave espacial, um conjunto de SC foi utilizado em uma Inertial Measurement Unit (Unidade de Medição Inercial - IMU). Os engenheiros estavam cientes do problema da GL, mas se recusaram a usar um quarto anel.^[4] Algumas das razões por trás desta decisão são aparentes na seguinte citação:

"Parece que as vantagens da SC redundate não compensam as vantagens de um equipamento simples e compacto, com a confiabilidade implícita de uma unidade com três graus de liberdade diretos."

Original {{{{{língua}}}}}: Apollo Lunar Surface Journal

— David Hoag

 Apollo Lunar Surface Journal

Eles preferiram uma solução alternativa de usar um indicador que seria acionado quando perto de um pitch de 85 graus.

"Perto deste ponto, em um loop fechado de estabilização, os motores de torque poderiam ser, teoricamente, comandados para girar a SC em 180 graus instantaneamente. Ao invés disso, no módulo lunar, o computador piscava um aviso de 'GL' a partir de 70 graus, e travava a IMU aos 85 graus."

Original {{{{{língua}}}}}: Apollo Lunar Surface Journal

— Paul Fjeld

 Apollo Lunar Surface Journal

Em vez de tentar conduzir as SC mais rápido do que elas podiam ir, o sistema simplesmente desistiu e congelou a plataforma. A partir deste ponto, a nave teria que ser movida manualmente para longe da posição de GL, e a plataforma teria que ser manualmente realinhada usando as estrelas como referência.^[5]

Depois que o módulo lunar havia pousado, Mike Collins, a bordo do módulo de comando brincou "que tal enviar-me uma quarta SC para o Natal?"

Na área de robótica, a GL é comumente chamada de "giro de pulso", devido ao uso de um pulsos de roll triplo em braços robóticos, onde os três eixos do pulso, yaw, pitch e roll, passam todos por um ponto comum.

Um exemplo de um giro de pulso, também chamado de singularidade do pulso, é quando o caminho o qual o robô está percorrendo faz com que o primeiro e o terceiro eixos do pulso do robô se alinhem. O segundo eixo do pulso, em seguida, tenta girar 180° instantaneamente para manter a orientação da mão. O resultado de uma singularidade pode ser bastante dramática e pode ter efeitos adversos sobre o braço do robô, sua mão, e o processo.

A importância de se evitar singularidades em robótica levou a American National Standard for Industrial Robots and Robot Systams — Safety Requirements à defini-la como "uma condição causada pelo alinhamento colinear de dois ou mais eixos de robô, resultando em movimentos e velocidades imprevisíveis do robô".^[6]

O problema da GL aparece quando se usa ângulos de Euler em matemática aplicada; desenvolvedores de programas de computador 3D, tais como modelagem 3D, sistemas de navegação inercial, e jogos eletrônicos devem tomar cuidado para evitá-la.

Em linguagem formal, a GL ocorre porque o mapa de ângulos de Euler para rotações (topologicamente, a partir do toro T³ para o espaço real projetivo RP³) não é um recobrimento – ele não é um homeomorfismo local em cada ponto, e assim, em alguns pontos, o posto (graus de liberdade) deve cair abaixo de 3, e é aí que ocorre a GL. Ângulos de Euler fornecem um meio de dar um descrição numérica para qualquer rotação no espaço tridimensional usando três números, mas não apenas esta descrição não é única, quanto também há alguns pontos onde nem todas as mudanças no espaço de destino (rotações) podem ser realizadas por meio de uma alteração no espaço de origem (ângulos de Euler). Esta é uma restrição topológica – não há cobertura de mapa a partir do toro 3D para o espaço real projetivo tridimensional; o único (não trivial), mapa abrangente é da esfera 3D, como no uso de quaterniões.

Para fazer uma comparação, todas as translações podem ser descritas por meio de três números ${\displaystyle x}$, ${\displaystyle y}$ e ${\displaystyle z}$, como a sucessão de três movimentos lineares consecutivos, ao longo de três eixos ortogonais ${\displaystyle X}$, ${\displaystyle Y}$ e ${\displaystyle Z}$. O mesmo vale para rotações: todas as rotações pode ser descritas por meio de três números ${\displaystyle \alpha }$, ${\displaystyle \beta }$, e ${\displaystyle \gamma }$, como a sucessão de três movimentos de rotação em torno de três eixos, que são perpendiculares um ao outro. Esta semelhança entre as coordenadas lineares e angulares faz os ângulos de Euler serem muito intuitivos, mas, infelizmente, eles sofrem com o problema da GL.

Uma rotação no espaço 3D pode ser representada numericamente com matrizes de várias maneiras. Uma dessas representações é:

${\displaystyle {\begin{aligned}R&={\begin{bmatrix}1&0&0\\0&\cos \alpha &-\sin \alpha \\0&\sin \alpha &\cos \alpha \end{bmatrix}}{\begin{bmatrix}\cos \beta &0&\sin \beta \\0&1&0\\-\sin \beta &0&\cos \beta \end{bmatrix}}{\begin{bmatrix}\cos \gamma &-\sin \gamma &0\\\sin \gamma &\cos \gamma &0\\0&0&1\end{bmatrix}}\end{aligned}}}$

Um exemplo interessante é quando ${\displaystyle \beta ={\tfrac {\pi }{2}}}$. Sabendo que ${\displaystyle \cos {\tfrac {\pi }{2}}=0}$ e ${\displaystyle \sin {\tfrac {\pi }{2}}=1}$, a expressão acima se torna igual a:

${\displaystyle {\begin{aligned}R&={\begin{bmatrix}1&0&0\\0&\cos \alpha &-\sin \alpha \\0&\sin \alpha &\cos \alpha \end{bmatrix}}{\begin{bmatrix}0&0&1\\0&1&0\\-1&0&0\end{bmatrix}}{\begin{bmatrix}\cos \gamma &-\sin \gamma &0\\\sin \gamma &\cos \gamma &0\\0&0&1\end{bmatrix}}\end{aligned}}}$

Realizando multiplicação de matrizes:

${\displaystyle {\begin{aligned}R&={\begin{bmatrix}0&0&1\\\sin \alpha &\cos \alpha &0\\-\cos \alpha &\sin \alpha &0\end{bmatrix}}{\begin{bmatrix}\cos \gamma &-\sin \gamma &0\\\sin \gamma &\cos \gamma &0\\0&0&1\end{bmatrix}}&={\begin{bmatrix}0&0&1\\\sin \alpha \cos \gamma +\cos \alpha \sin \gamma &-\sin \alpha \sin \gamma +\cos \alpha \cos \gamma &0\\-\cos \alpha \cos \gamma +\sin \alpha \sin \gamma &\cos \alpha \sin \gamma +\sin \alpha \cos \gamma &0\end{bmatrix}}\end{aligned}}}$

E, finalmente, usando fórmulas trigonométricas:

${\displaystyle {\begin{aligned}R&={\begin{bmatrix}0&0&1\\\sin(\alpha +\gamma )&\cos(\alpha +\gamma )&0\\-\cos(\alpha +\gamma )&\sin(\alpha +\gamma )&0\end{bmatrix}}\end{aligned}}}$

Alterar os valores de ${\displaystyle \alpha }$ e ${\displaystyle \gamma }$ na matriz acima tem os mesmos efeitos: o ângulo de rotação ${\displaystyle \alpha +\gamma }$ muda, mas o eixo de rotação permanece na direção ${\displaystyle Z}$: a última coluna e a primeira linha da matriz não vão mudar. A única solução para ${\displaystyle \alpha }$ e ${\displaystyle \gamma }$ recuperarem papéis diferentes é mudar ${\displaystyle \beta }$.

É possível imaginar um avião orientado com os ângulos mencionados acima usando a convenção X-Y-Z. Neste caso, o primeiro ângulo - ${\displaystyle \alpha }$ é o pitch. O yaw é, definido como ${\displaystyle {\tfrac {\pi }{2}}}$ e a rotação final - ${\displaystyle \gamma }$ - é, novamente, o pitch do avião. Por causa da GL, o avião perdeu um dos graus de liberdade - neste caso, a capacidade de rolar (roll).

Também é possível escolher outra convenção para representar uma rotação com uma matriz usando ângulos de Euler usando a convenção X-Y-Z acima, e também escolher outros intervalos de variação para os ângulos, mas no fim, há sempre pelo menos um valor para o qual um grau de liberdade é perdido.

O problema da GL não torna os ângulos de Euler "inválidos" (eles sempre servem como um sistema de coordenadas bem definido), mas torna-os impróprios para algumas aplicações práticas.

A causa da GL é querer representar orientação como três rotações, usando ângulos de Euler. Uma possível solução é, portanto, representar a orientação de outra forma. Isto poderia ser feito com uma matriz de rotação, um quaternião, ou outra representação similar, que trate a orientação como um valor, em vez de três valores separados e relacionados. Dada tal representação, o usuário armazena a orientação como um valor. Para aplicar alterações angulares, a orientação é modificada por um ângulo delta ao redor de um eixo de rotação. A orientação resultante deve ser normalizada para evitar que erros de ponto flutuante se acumulem depois de transformações sucessivas. Para matrizes, normalizar o resultado requer a conversão da matriz em sua mais próxima representação ortonormal. Para quaterniões, normalização requer a realização de normalização de quaterniões.

• Quaterniões
• Sistema de navegação inercial
• Eixos do avião