Pyraminx – Wikipédia, a enciclopédia livre

O Pyraminx ( /ˈpɪrəmɪŋks/) é um quebra-cabeça no formato de um tetraedro regular no estilo do Cubo de Rubik. Ele foi criado e patenteado por Uwe Mèffert depois do cubo de 3 camadas original de Erno Rubik, e introduzido pela Tomy Brinquedos do Japão (na época, a 3ª maior empresa de brinquedos do mundo), em 1981.^[1]

O Pyraminx foi idealizado por Mèffert em 1970. Ele não fez nada com a sua concepção até 1981, quando a levou para Hong Kong para ser produzida. Uwe gosta de dizer que se não fosse por Erno Rubik ter inventado o cubo, seu Pyraminx nunca teria sido produzido.

O Pyraminx é um quebra-cabeça na forma de um tetraedro regular dividido em 4 peças axiais, 6 arestas, e 4 pontas triviais. Ele pode ser torcido ao longo de seus cortes para permutar suas peças. As peças axiais têm forma octaédrica, embora isso não seja imediatamente óbvio, e só podem girar em torno do eixo ao qual estão ligadas. As 6 arestas podem ser permutadas livremente. As pontas triviais são assim chamadas pois elas podem ser torcidas de forma independente de todas as outras peças, tornando-as triviais de serem movidas para a posição resolvida.

Meffert também produz um quebra-cabeça semelhante chamado de Tetraminx, que é o mesmo que o Pyraminx, mas com as pontas triviais removidas, transformando o quebra-cabeça em um tetraedro truncado.

O propósito do Pyraminx é misturar as cores e, em seguida, restaurá-las para sua configuração original.

As 4 pontas triviais podem ser facilmente rodadas para alinhar com suas respectivas peças axiais; e as peças axiais também são facilmente giradas de modo que as suas cores se alinhem umas com as outras. Isso deixa apenas as 6 arestas como o verdadeiro desafio do quebra-cabeça. Elas podem ser resolvidas aplicando repetidamente duas sequências de 4-torções, que são imagens espelhadas uma da outra. Estas sequências permutam 3 arestas de cada vez, e alteram as suas orientações de forma diferente, de modo que uma combinação de ambas as sequências é suficiente para resolver o quebra-cabeça. No entanto, soluções mais eficientes (que requerem um número menor de torções no total) são geralmente disponíveis (veja abaixo).

A torção de qualquer peça axial é independente das outras três, assim como é o caso das pontas. As seis arestas podem ser colocadas em 6!/2 posições e orientadas em 2⁵ maneiras, contando com as paridades. Multiplicando isso pelo fator 3⁸  devido às peças axiais temos 75,582,720 combinações possíveis. No entanto, resolver as peças triviais reduz as possibilidades para 933,120, que também é o número de padrões possíveis no Tetraminx. Resolver as peças axiais reduz o número ainda mais, a apenas 11,520 combinações, tornando este um quebra-cabeça relativamente simples de resolver.

O número máximo de torções necessárias para resolver o Pyraminx é 11. Há 933,120 posições diferentes (desconsiderando a rotação das pontas triviais), um número que é suficientemente pequeno para permitir que um computador busque as melhores soluções. A tabela abaixo resume o resultado de uma busca, informando o número p de posições que requerem n torções para resolver o Pyraminx:

n	0	1	2	3	4	5	6	7	8	9	10	11
p	1	8	48	288	1728	9896	51808	220111	480467	166276	2457	32

O atual recorde mundial para uma única resolução do Pyraminx é de 0.91 segundos, conseguido por Dominik Górny no Byczy Cube Race 2018. Tymon Kolasiński tem o recorde da maior média de 5 (com as resoluções mais rápida e mais lenta desconsideradas) com 1.86 segundos na Grudziądz Open 2019.^[2]

Há muitos métodos para a solução de um Pyraminx. Eles podem ser divididos em dois grupos.

1. V primeiro - Nesses métodos, duas ou três arestas, e não um lado, são resolvidas primeiro. Um conjunto de algoritmos chamado de LL algs (do inglês "last layer algorithms", ou algoritmos da última camada), são usados para resolver o restante do quebra-cabeça.
2. Topo primeiro - Nesses métodos, um bloco em cima, que consiste de três arestas em torno de um canto, é resolvido primeiro e o restante é resolvido usando um conjunto de algoritmos.

1. Camada por Camada - Neste método, uma face com todas as arestas orientadas no lugar certo (i.e. uma camada) é resolvida e, em seguida, o restante do quebra-cabeça é resolvido usando 5 algoritmos especiais para este método.
2. L4E - L4E (do inglês "last 4 edges," ou 4 últimas arestas) é muito semelhante ao camada por camada. A única diferença é que duas arestas são resolvidas em torno de três eixos, e o resto é feito por um conjunto de algoritmos.
3. L4E intuitivo - Um método semelhante ao L4E, como o nome sugere, em que muita visualização é necessária. O conjunto de algoritmos mencionados no método anterior não são memorizados. Em vez disso, as pessoas resolvem intuitivamente cada caso, antecipando o movimento das peças. Este é o método mais avançado de V primeiro.

1. Um Giro - Este método usa duas arestas em torno de um eixo resolvidas e a terceira borda invertida. Há um total de seis casos após esta etapa, que são resolvidos com algoritmos memorizados. O terceiro passo envolve a utilização de um conjunto comum de algoritmos para todos os métodos de topo primeiro, também chamado de "fechadura da última camada", que envolve 5 algoritmos, quatro deles sendo espelhos uns dos outros.
2. Fechadura - Este método usa duas arestas no lugar certo, em torno de um centro, e a terceira aresta não está nem na posição ou na orientação correta. Os centros da quarta cor, são resolvidos usando a aresta não orientada (chamada de fechadura). O último passo é resolvido com o método da fechadura da última camada.
3. OKA - neste método, uma aresta é orientada em torno de duas arestas no lugar errado, mas uma das arestas que está no lugar errado pertence ao bloco em si. A última aresta é encontrada na camada inferior e um algoritmo simples é executado para colocá-la no lugar certo, seguida pelo buraco da fechadura da última camada.

Profissionais de Pyraminx como Drew Brads normalmente aprendem todos os métodos, e observando um caso, decidem qual o método que melhor se adapta à situação.

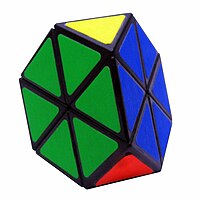
Existem diversas variações deste quebra-cabeça. O mais simples, Tetraminx, é equivalente ao Pyraminx mas sem as pontas (ver foto). Existem também versões "de ordem superior", Master Pyraminx (4x) (ver foto) e o Professor Pyraminx (5x).

O Master Pyraminx tem 4 camadas e 16 triângulos-por-face (em comparação com 3 camadas e 9 triângulos-por-face do original). Esta versão tem cerca de 2.17225 × 10¹⁷ combinações.^[3][4] O Master Pyraminx tem:

• 4 "pontas" (como o Pyraminx original)
• 4 "meios axiais" (como o Pyraminx original)
• 4 "centros" (semelhante ao Cubo de Rubik, nenhum no Pyraminx original)
• 6 "arestas internas" (semelhante ao Cubo de Rubik, nenhum no Pyraminx original)
• 12 "arestas" (2 vezes a mais do que as 6 do Pyraminx original)

Em resumo, o Master Pyraminx tem 30 peças "manipuláveis". No entanto, como o original, 8 das peças (as pontas e meios axiais) têm posições fixas em relação umas às outras e só podem ser giradas no lugar. Além disso, os 4 centros são fixos e só podem girar (como o Cubo de Rubik). Por isso, são apenas 18 (30-8-4) peças "verdadeiramente móveis". Como este número é 10% menor do que as 20 peças "verdadeiramente móveis" do Cubo de Rubik, não deve ser nenhuma surpresa que o Master Pyraminx tenha cerca de 200 vezes menos combinações que um Cubo de Rubik (cerca de 4.3252 × 10^19[5]).

• Cubo de Rubik
• Skewb

• Jaap do Pyraminx e quebra-cabeças relacionados a página, com a solução
• Pyraminx solução de PuzzleSolver
• Uma solução para o Pyraminx^{[ligação inativa]} por Jonathan Bowen
• Um eficiente e fácil de seguir solução favorecida pela velocidade solucionadores
• Padrões de Uma coleção de padrões bonitos para o Pyraminx