Simetria rotacional – Wikipédia, a enciclopédia livre

A simetria rotacional, também conhecida como simetria radial na geometria, é a propriedade que uma forma tem quando parece a mesma após alguma rotação por uma volta parcial. O grau de simetria rotacional de um objeto é o número de orientações distintas nas quais ele parece exatamente o mesmo para cada rotação.

Certos objetos geométricos são parcialmente simétricos quando girados em certos ângulos, como quadrados girados 90°, no entanto, os únicos objetos geométricos que são totalmente simétricos rotacionalmente em qualquer ângulo são esferas, círculos e outros esferoides.^[1][2]

Formalmente, a simetria rotacional é a simetria em relação a algumas ou todas as rotações no espaço euclidiano m-dimensional. As rotações são isometrias diretas [en], isto é, isometrias que preservam a orientação. Portanto, um grupo de simetria de simetria rotacional é um subgrupo de E⁺(m) (ver grupo euclidiano).

A simetria com relação a todas as rotações sobre todos os pontos implica simetria translacional com relação a todas as translações, de modo que o espaço é homogêneo e o grupo de simetria é todo o E(m). Com a noção modificada de simetria para campos vetoriais [en], o grupo de simetria também pode ser E+(m).

Para simetria em relação às rotações em torno de um ponto, podemos tomar esse ponto como origem. Estas rotações formam o grupo ortogonal especial SO(m), o grupo de [[Matriz ortogonal|matrizes (arranjos) ortogonais m×m com determinante 1. Para m = 3 este é o grupo de rotação SO(3).

Em outra definição da palavra, o grupo de rotação de um objeto é o grupo de simetria dentro de E⁺(n), o grupo de isometrias diretas; em outras palavras, a interseção do grupo de simetria total e o grupo de isometrias diretas. Para objetos quirais é o mesmo que o grupo de simetria completo.

As leis da física são SO(3)-invariantes se não distinguirem diferentes direções no espaço. Por causa do teorema de Noether, a simetria rotacional de um sistema físico é equivalente à lei de conservação do momento angular.

Simetria rotacional de ordem n, também chamada de simetria rotacional de n dobra(s), ou simetria rotacional discreta de enésima ordem, em relação a um ponto particular (em 2D) ou eixo (em 3D) significa que a rotação em um ângulo de 360°/n (180°, 120°, 90°, 72°, 60°, 51 3⁄7°, etc.) não altera o objeto. Uma simetria de "1 dobra" não é, ou é sem, simetria (todos os objetos parecem iguais após uma rotação de 360°).

A notação para simetria de n dobras é C_n ou simplesmente "n". O grupo de simetria real é especificado pelo ponto ou eixo de simetria, juntamente com o n. Para cada ponto ou eixo de simetria, o tipo de grupo abstrato é grupo cíclico de ordem n, Z_n. Embora para este último também seja usada a notação C_n, o C_n geométrico e o C_n abstrato devem ser distinguidos: existem outros grupos de simetria do mesmo tipo de grupo abstrato que são geometricamente diferentes .

O domínio fundamental [en] é um setor de 360°/n.

Exemplos sem simetria de reflexão adicional:

• n = 2, 180°: a díade; as letras Z, N e S; os contornos, embora não as cores, do símbolo do yin e yang; a bandeira da união (dividida ao longo da diagonal da bandeira e girada sobre o ponto central da bandeira)
• n = 3, 120°: tríade, tríscele, anéis borromeanos; às vezes o termo simetria trilateral é usado;
• n = 4, 90°: tétrade, suástica
• n = 6, 60°: héxade, Estrela de Davi (este tem simetria de reflexão adicional)
• n = 8, 45°: óctade, teto de muqarnas octogonal gerado por computador (G.C.)

C_n é o grupo de rotação de um polígono regular de n lados em 2D e de uma pirâmide regular de n lados em 3D.

Se houver, por exemplo, simetria rotacional em relação a um ângulo de 100°, então também em relação a um de 20°, o máximo divisor comum de 100° e 360°.

Uma hélice é um objeto 3D típico com simetria rotacional (possivelmente também com eixos perpendiculares), mas sem simetria de espelho.

C2 (mais)	C3 (mais)	C4 (mais)	C5 (mais)	C6 (mais)
Fractal de pêndulo duplo	Sinal de trânsito de rotatória		Estrela do bicentenário dos Estados Unidos [en]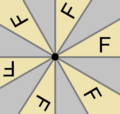
A posição inicial em shogi	Design dos chifres de bebida [en] interligados da pedra de Snoldelev [en]

Para simetria discreta [en] com múltiplos eixos de simetria passando pelo mesmo ponto, existem as seguintes possibilidades:

• Além de um eixo de n dobras, n eixos perpendiculares de duas dobras: os grupos de diedros D_n de ordem 2n (n ≥ 2). Este é o grupo de rotação de um prisma regular ou uma bipirâmide regular. Embora a mesma notação seja usada, o D_n geométrico e o D_n abstrato devem ser distinguidos: existem outros grupos de simetria do mesmo tipo de grupo abstrato que são geometricamente diferentes.
• Eixos de 4×3 dobras e 3×2 dobras: o grupo de rotação T de ordem 12 de um tetraedro regular. O grupo é isomórfico ao grupo alternante A₄.
• Eixos de 3×4 dobras, 4×3 dobras e 6×2 dobras: o grupo de rotação O de ordem 24 de um cubo e um octaedro regular. O grupo é isomórfico ao grupo simétrico S₄.
• Eixos de 6×5 dobras, 10×3 dobras e 15×2 dobras: o grupo de rotação I de ordem 60 de um dodecaedro e um icosaedro. O grupo é isomórfico ao grupo alternante A₅. O grupo contém 10 versões de D₃ e 6 versões de D₅ (simetrias rotacionais como prismas e antiprismas).

No caso dos sólidos platônicos, os eixos duplos passam pelos pontos médios das arestas opostas, e o número deles é metade do número de arestas. Os outros eixos passam por vértices opostos e por centros de faces opostas, exceto no caso do tetraedro, onde os eixos triplos passam cada um por um vértice e o centro de uma face.

A simetria rotacional em relação a qualquer ângulo é, em duas dimensões, simetria circular. O domínio fundamental é uma meia-linha/reta.

Em três dimensões, podemos distinguir simetria cilíndrica e simetria esférica (sem alteração ao girar em torno de um eixo ou para qualquer rotação). Ou seja, nenhuma dependência do ângulo usando coordenadas cilíndricas e nenhuma dependência de qualquer ângulo usando coordenadas esféricas. O domínio fundamental é um semiplano através do eixo e uma semirreta radial, respectivamente. Axisimétrico ou axissimétrico são adjetivos que se referem a um objeto com simetria cilíndrica, ou axisimetria (ou seja, simetria rotacional em relação a um eixo central) como um donut (toro). Um exemplo de simetria esférica aproximada é a Terra (no que diz respeito à densidade e outras propriedades físicas e químicas).

Em 4D, a simetria rotacional contínua ou discreta sobre um plano corresponde à simetria rotacional 2D correspondente em cada plano perpendicular, sobre o ponto de interseção. Um objeto também pode ter simetria rotacional em torno de dois planos perpendiculares, por exemplo, se for o produto cartesiano de duas figuras 2D rotacionalmente simétricas, como no caso de, por exemplo, o duocilindro e vários duoprismas [en] regulares.

Disposição dentro de uma célula primitiva [en] de rotocentros de 2 e 4 dobras. Um domínio fundamental [en] é indicado em amarelo.

Arranjo dentro de uma célula primitiva de rotocentros de 2, 3 e 6 dobras, sozinhos ou em combinação (considere o símbolo de 6 dobras como uma combinação de um símbolo de 2 e um símbolo de 3 dobras); apenas no caso de simetria de 2 dobras, a forma do paralelogramo pode ser diferente. Para o caso p6, um domínio fundamental é indicado em amarelo.

A simetria rotacional de 2 dobras junto com a simetria translacional única é um dos grupos de friso [en]. Existem dois rotocentros por célula primitiva [en].

Juntamente com a dupla simetria translacional, os grupos de rotação são os seguintes grupos de papel de parede [en], com eixos por célula primitiva:

• p2 (2222): 4×2 dobras; grupo de rotação de uma rede paralelogramma, retangular e rômbica.
• p3 (333): 3×3 dobras; não o grupo de rotação de qualquer rede (toda rede é a mesma de cabeça para baixo, mas isso não se aplica a esta simetria); é, por exemplo, o grupo de rotação do ladrilho triangular regular com os triângulos equiláteros coloridos alternadamente.
• p4 (442): 2×4 dobras, 2×2 dobras; grupo de rotação de uma rede quadrada.
• p6 (632): 1×6 dobras, 2×3 dobras, 3×2 dobras; grupo de rotação de uma rede hexagonal.
• Rotocentros de 2 dobras (incluindo possíveis de 4 e 6 dobras), se presentes, formam a translação de uma rede igual à rede translacional, dimensionada por um fator 1/2. No caso de simetria translacional em uma dimensão, aplica-se uma propriedade semelhante, embora o termo "rede" não se aplique.
• Rotocentros de 3 dobras (incluindo possíveis de 6 dobras), se presentes, formam uma rede hexagonal regular igual à rede translacional, girada em 30° (ou equivalente a 90°) e dimensionada por um fator ${\displaystyle {\frac {1}{3}}{\sqrt {3}}}$
• Rotocentros de 4 dobras, se presentes, formam uma rede quadrada regular igual à rede translacional, girada em 45° e dimensionada por um fator ${\displaystyle {\frac {1}{2}}{\sqrt {2}}}$
• Rotocentros de 6 dobras, se presentes, formam uma rede hexagonal regular que é a tradução da rede translacional.

A escala de uma rede divide o número de pontos por unidade de área pelo quadrado do fator de escala. Portanto, o número de rotocentros de 2, 3, 4 e 6 dobras por célula primitiva é 4, 3, 2 e 1, respectivamente, novamente incluindo 4 dobras como um caso especial de 2 dobras, etc.

Simetria rotacional de 3 dobras em um ponto e de 2 dobras em outro (ou idem em 3D em relação a eixos paralelos) implica grupo de rotação p6, ou seja, simetria translacional dupla e simetria rotacional de 6 dobras em algum ponto (ou, em 3D, eixo paralelo). A distância de translação para a simetria gerada por um desses pares de rotocentros é ${\displaystyle 2{\sqrt {3}}}$ vezes a distância deles.

Euclidean plane	Hyperbolic plane
Telha triangular Hexakis [en], um exemplo de p6, [6,3]+, (632) (com cores) e p6m, [6,3], (*632) (sem cores); as linhas são eixos de reflexão se as cores forem ignoradas, e um tipo especial de eixo de simetria se as cores não forem ignoradas: a reflexão reverte as cores. As grades de linhas retangulares em três orientações podem ser distinguidas.	Kisrhombille de ordem 3-7 [en], um exemplo de simetria [7,3]+ (732) e [7,3], (*732) (sem cores)

• Weyl, Hermann (1982) [1952 l]. Symmetry (em inglês). Princeton: Princeton university press. ISBN 0-691-02374-3 

• Media relacionados com Simetria rotacional no Wikimedia Commons
• Exemplos de simetria de rotação (em inglês) em Math is fun