Скобка Кауффмана — Википедия

Скобка Кауффмана — полиномиальный инвариант оснащённого зацепления. Хотя он и не является инвариантом узла или зацепления (без оснащения он не является инвариантным относительно движения Рейдемейстера I типа), подходящая «нормализация» позволяет превратить его в вариант знаменитого инварианта — полинома Джонса.

Скобка Кауффмана была рассмотрена Луисом Кауффманом в 1987 году^[1].

Скобка Кауффмана <L> определяется по произвольной (неориентированной) диаграмме узла L в соответствии со следующими правилами:

• ${\displaystyle \langle O\rangle =1}$, где ${\displaystyle O}$ — стандартная диаграмма тривиального узла
• 
• ${\displaystyle \langle O\cup L\rangle =(-A^{2}-A^{-2})\langle L\rangle }$

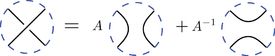
Диаграммы зацеплений во втором правиле совпадают везде, кроме небольшого диска — окрестности перекрёстка — где они устроены так, как показано. Третье правило утверждает, что, добавляя к диаграмме компоненту-окружность, не пересекающую остальную часть диаграммы, мы умножаем скобку на ${\displaystyle -A^{2}-A^{-2}}$.

• В. В. Прасолов, А. Б. Сосинский, Узлы, зацепления, косы и трехмерные многообразия. — М.: МЦНМО, 1997.

• mathworld

Это заготовка статьи по математике. Помогите Википедии, дополнив её.