Diffraktion – Wikipedia

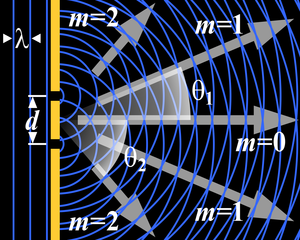
Diffraktion (latin diffractio, av diffringere, sönderbryta) är böjning av ljus.

Om parallellt ljus får falla på en öppning i en ogenomtränglig vägg, kommer strålarna att breda ut sig så att den bild av öppningen som uppfångas på en skärm blir större än den skulle vara om strålarna fortplantade sig helt rätlinjigt. Det verkar alltså som om ljusstrålarna skulle böjas vid kanterna av öppningen. Förklaringen till detta fenomen hämtas ur teorin om ljusets vågnatur. Enligt Huygens princip kan varje partikel inom en ljusvåg betraktas såsom medelpunkt för ett nytt vågsystem, som sänder ut strålar i alla riktningar, och strålar utgår från öppningen.

Låt ab vara en mångfaldigt förstorad öppning, genom vilken parallella ljusstrålar infaller i ett mörkt rum. Nära öppningen, som i detta fall utgörs av en mycket smal springa, ligger de särskilda punkterna i öppningen ungefär lika långt från ljuskällan och måste följaktligen befinna sig i nästan samma svängningstillstånd eller tillsammans bilda delar av samma ljusvåg. Strålar utgår alltså från varje punkt i öppningen ab. Punkten c, som ligger på den mot ab vinkelräta mittlinjen de, ligger också symmetriskt, så att en stråle genom c på ena sidan om cd motsvaras av en likadan stråle på andra sidan, som tillryggalagt lika lång väg från utgångspunkten och alltså måste befinna sig i samma fas eller svängningstillstånd och därför förstärka den andra strålen. I punkten c måste det alltså vara så att strålarna parvis understödjer (förstärker) varandra, så att ett starkt ljus uppkommer, om det till exempel uppfångas på en skärm, YZ.

På sidan om c blir förhållandet ett annat. Om till exempel i punkten n, skillnaden mellan de yttersta strålarna, an - bn = aq, är en hel ljusvågs längd, så skiljer sig strålarna an och ”dn” med en halv våglängd och utsläcker därför varandra. Varje stråle som utgår från en punkt på ”ad” i riktning mot n upphävs på samma sätt av en stråle som utgår från motsvarande punkt på ”db”. Detta gör att punkten n blir mörk. Utanför ”n” börjar ljuset åter att framträda och blir intensivare ända till en punkt m, som ligger så att skillnaden mellan de yttersta strålarna, am-bm är tre halva våglängder. I punkten n1, där skillnaden an1-bn1 är två hela våglängder, blir det återigen mörkt, av samma skäl som vid n, och så vidare.

Ljusminima uppstår alltså i alla punkter där vägskillnaden mellan de yttersta strålarna är en hel våglängd för ljuset eller flera hela våglängder. Maxima uppstår mellan punkterna med minima, på de ställen där vägskillnaderna är en udda multipel av en halv våglängd ((2N + 1) * L/2, där N är ett heltal). Att dessa maxima blir mindre intensiva längre ut åt sidorna kan kanske inses utan ytterligare utredning. I till exempel punkten m, där skillnaden mellan de yttersta strålarna antogs vara tre halva våglängder, upphäver strålarna varandra parvis inom två tredjedelar av strålknippet, så att endast den återstående tredjedelen kan verka. I nästa ljusmaximum, med fasskillnaden fem halva våglängder, blir den verksamma delen endast en femtedel, och så vidare.

Om öppningen har en annan form uppstår andra figurer. Är den rektangulär, blir bilden naturligtvis en kombination av två sådana som den avbildade, lagda vinkelrätt över varandra. En rund öppning ger i mitten en ljus fläck, omgiven av omväxlande mörka och ljusa koncentriska ringar. Allt detta gäller endast under förutsättningen att det infallande ljuset är homogent, det vill säga enfärgat. Om till exempel solljus får falla genom öppningen får strålar med olika våglängd och följaktligen av olika färg inte sina ljusmaxima i samma punkter. Utanför det mittersta maximat blir det inte vitt någonstans. Inte heller blir det fullständigt mörkt i någon punkt. Det blir ett varierande mönster med olika färger (böjningsfärger) i olika punkter. I varje punkt är någon viss färg dominerande.

Om ljuset får falla in genom flera parallella öppningar i samma skärm, så frambringar varje öppning böjningsfenomenen var för sig, på samma sätt som beskrivits ovan för en enda öppning. Böjningsfigurerna kommer då att delvis falla över varandra och det uppstår samverkan interferens av strålar, inte endast från samma, utan också från olika öppningar. Om öppningarnas antal är mycket stort, som till exempel när man använder ett fint gitter, kommer fältet att visa sig mörkt, men genomskuret av smala, med öppningarna parallella ljusa linjer, som faller olika långt ifrån varandra, allt efter det infallande ljusets färg. Om man använder vitt ljus (som inte är homogent) så får mitten en skarp vit linje, på båda sidorna omgiven av mörka fält. Utanför dessa uppkommer på vardera sidan flera spektra, med den violetta färgen innerst och den röda ytterst. Om det infallande ljuset saknar strålar av någon viss våglängd, uppstår på motsvarande ställe i böjningsspektrum en mörk linje. I böjningsspektrum finns alltså inte bara samma följd av färger som i det spektrum som åstadkommes genom brytning i ett prisma. Det blir också samma följd av mörka linjer, de så kallade Fraunhoferska linjerna.

Kännedom om ljusets böjningsfenomenet hade stor betydelse för experiment som på ett lysande sätt gav stöd för vibrationsteorin.

Böjningsfenomenet gjorde också att man tidigt kunde utforma en säker metod att avgöra våglängden för ljus. Med hjälp av figuren kan man inse hur en sådan bestämning är möjlig. Ovan antog vi att skillnaden mellan an och bn i punkten n är två halva våglängder. Denna skillnad (det vill säga sträckan aq) kan man beräkna ur den lilla triangeln aqb, där sidan ab kan uppmätas. Likaså kan man mäta vinkeln abq, som är lika med cdn. Utöver att bestämma springans bredd, behöver man alltså endast mäta vinkeln mellan den infallande eller utan böjning fortplantade strålen och strålen till någon av minimumpunkterna. Denna vinkelmätning sker lättast och säkrast med hjälp av en teodolit. De mest exakta mätningarna av ljusets våglängder får man inte genom att observera läget av de genom en enda öppning alstrade maxima och minima av ljus, utan genom motsvarande iakttagelse på de mörka linjerna i böjningsspektrum alstras av det sammansatta (ofärgade) ljusets gång genom en mängd parallella, ytterst smala öppningar som tillsammans bildar ett så kallat gitter (böjningsgitter, böjningsgaller). Spektrumet brukar därför också benämnas gitterspektrum (böjningsspektrum). Detta spektrum kallas också normalspektrum, till skillnad från de med brytande prismor framkallade brytningsspektra, eftersom läget av de olika färgerna i gitterspektrum bestäms endast av deras ljus-våglängd och inte alls beror på vilket ämne gittret är gjort av, medan läget av färgerna i ett brytningsspektrum beror också på materialet i det brytande prismat. Gittret kan till exempel bestå av linjer som är uppdragna på en glas- eller metallplatta. I det senare fallet studeras det reflekterade ljuset.

Tillfällen att få se böjningsfenomen av en eller annan form får man lätt, till exempel om man ser genom fanet på en fjäder emot ett ljus, om man med nästan slutna ögonlock, således genom ögonhåren eller genom en gardin, vävd med parallella trådar med lika avstånd, ser mot en avlägsen, starkt lysande punkt, om man ser mot solen genom spindelväv eller genom en glasskiva beströdd med så kallad nikt (semen lycopodii). De färger, som uppkommer genom diffraktion, kallas diffraktions- eller böjningsfärger.

Ljusets böjningsfenomen studerades redan under senare hälften av 1600-talet av Grimaldi. Isaac Newton upprepade en del av dennes försök, men lyckades inte formulera någon förklaring. I början av 1800-talet angav Thomas Young interferensen mellan strålarna som orsaken till böjningsfenomenen och Augustin Fresnel utförde den teoretiska analysen. Friedrich Magnus Schwerd i Speier, gjorde fullständiga beräkningar av alla de figurer som uppstår när ljuset går genom små öppningar av olika form.

• Optiska brytningsfel

• Diffraktion i Nordisk familjebok (andra upplagan, 1907)

• Wikimedia Commons har media som rör Diffraktion.
  Bilder & media