Магнітогідродинамічна енергетика — Вікіпедія
Магнітогідродинамічна енергетика (англ. magnetohydrodynamic power) — наука та галузь, частина молекулярної гідроенергетики, яка вивчає магнітогідродинамічні явища в рідинних дисперсних системах та використовує енергетичні перетворення кінетика — електрика під впливом магнітного поля з метою вироблення, накопичення, транспортування та розподілу електричної енергії.

У фундаменті магнітогідродинамічної енергетики лежать атомно-молекулярний та йонно-молекулярний принципи побудови речовини. Перший принцип характеризує дискретність або перервність будови речовини, другий принцип розкриває стан електролітичних розчинів та взаємодію йонів з молекулами розчинника. Кінетичні та електричні властивості молекулярних частинок електроліту спричиняють в магнітному полі магнітогідродинамічні явища, які є джерелом електричної енергії.
Ключовими поняттями та об'єктами досліджень магнітогідродинамічної енергетики є магнетизм, магніти, електролітичні розчини, магнітогідродинамічні технології (способи) та магнітогідродинамічні системи (засоби) перетворення потенціальної та кінетичної енергії молекул, атомів, йонів, інших малих частинок речовини в електричну енергію. Як джерела відновлюваної енергії досліджуються, в першу чергу, природні середовища, зокрема, гідросфера й процеси, що в ній протікають, а також сили, які супроводжують ці процеси.
Магнітогідродинамічні технології та системи є малоінерційними прямими способами та засобами виробництва електричного струму, бо в енергетичних перетвореннях не використовуються рухомі масивні елементи — ротори. Робота систем базується на властивостях йонів, інших малих заряджених частинок речовини в рідинних дисперсних системах взаємодіяти між собою та з молекулами оточуючого середовища, змінювати термодинамічні параметри середовища й утворювати електричні поля під впливом зовнішнього магнітного поля. У результаті взаємодії рухомої йонізованої рідини з магнітним полем, відповідно до закону електромагнітної індукції Майкла Фарадея, виникає електричне поле, яке діє перпендикулярно напряму руху заряджених частинок та напряму силового магнітного поля й формує електричний струм у вбудованих поряд електродах-провідниках.
Науково-технологічною базою магнітогідродинамічної енергетики є досягнення молекулярної фізики, фізичної хімії, хімії та фізики поверхні, електродинаміки, квантової теорії речовини та поля, термодинаміки й, звісно ж, магнітогідродинаміки.[1]
У ХІХ ст. отримують розвиток і широко застосовуються в аналізі фізичних та хімічних систем положення термодинаміки, статистичної механіки, динаміки та рівноваги. Досліджується вплив міжмолекулярних сил на фізичні властивості матеріалів, зокрема, на пластичність, деформацію, поверхневий натяг у рідині та електропровідність. Вивчається електрохімія мембран. Витоки магнітогідродинамічної енергетики слід шукати у витоках електрики, магнетизму й, звісно ж, магнітогідродинаміки. Перший МГД-генератор для вимірювання об'ємних витрат рідини був створений у 1832 році Майклом Фарадеєм. Проте, вираз «магнітогідродинаміка» в 1942 році вперше застосував шведський фізик та астроном Ганнес Альфвен, який досліджував наведення електричного струму при взаємодії солоної води та магнітного поля.[2][3] При розрахунках МГД-систем використовуються взаємозв'язані рівняння гідродинаміки французького інженера Клода-Луї Нав'є та британського математика і фізика Джорджа Габріеля Стокса, які пояснюють рух нестисливої в'язкої рідини, а також рівняння, виведені шотландським фізиком Джеймсом Максвеллом для електромагнітного поля. У своїй основі магнітогідродинаміка спирається на досягнення квантової механіки, молекулярної фізики та електродинаміки, що враховують молекулярну та йонну дискретну природу рідини.
Суттєвий внесок у розуміння магнітних явищ зробили творці квантової теорії. Німецький фізик-теоретик Вернер Гейзенберг застосував принципи квантової механіки до проблем феромагнетизму. Рівняннями британського фізика Поля Дірака були підтверджені магнітні властивості електрона (магнітний момент). Англійський фізик та хімік-теоретик Джон Едвард Леннард-Джонс дослідив парамагнетизм двоатомних молекул, зокрема, оксигену і є основоположником методу молекулярних орбіталей. Лундквіст,[4] Суттон та Шерман[5], Хюгз та Юнг[6] також були в числі теоретиків-першопроходців, чиї фундаментальні дослідження визначили прикладні напрямки розвитку магнітогідродинаміки. Проекти магнітогідродинамічних генераторів на спалюванні органічного палива у свій час інтенсивно досліджувалися в США, СРСР, Індії та Японії. Девід Елліот[7] запропонував використовувати як електропровідне середовище рідкий метал, точніше, суміш металів Na (78 %) та K (22 %). Ним розглядалися також схеми МГД-генераторів з ядерним реактором. На базі ракетних двигунів були створені пульсуючі МГД-генератори для геофізичних досліджень.
В основі магнітних явищ в речовині лежать квантові властивості мікрочастинок, які проявляються в електромагнітній взаємодії. Згідно теорії спіну та принципу виключення Паулі, джерелом магнетизму є струм та магнітні моменти спінів в елементарних частинках. Магнітний момент — векторна величина, що характеризує взаємодію тіла з магнітним полем. Магнітний момент вимірюється в А·м2 або Дж/Тл (СІ), або в ерг/Гс (СГС), 1 ерг/Гс = 10−3 Дж/Тл.
Магнітний момент μ [А·м2] в загальному вигляді визначається з виразу для моменту сили τ [Н·м], діючої на частку в магнітному полі, яке має магнітну індукцію B [Тл],
τ = μ × B.
Магнітний момент атома визначається спіном електронів, рухом електронів довкола ядра (орбітальний момент) та магнітним моментом атомного ядра. Для окремих елементарних частинок це прояв їх спінового магнітного моменту.
Якщо магнітне поле, створене струмами провідника, внести в ту чи іншу речовину, то воно зміниться. Будь-яка речовина є магнетиком і може намагнічуватись під дією магнітного поля, тобто набувати магнітного моменту. Намагнічена речовина створює магнітне поле індукцією B1 [Тл], яке разом з первинним полем індукцією B0 [Тл] створюють загальне магнітне поле з індукцією B,
B = B1 — B0.
Магнітне поле не має магнітних зарядів, для поля B справедлива теорема Гауса, тобто лінії магнітної індукції B є неперервними,
∫B·dS = 0.
Згідно гіпотези Ампера, в молекулах речовини циркулюють молекулярні струми. Кожен такий струм володіє магнітним моментом і створює в навколишньому середовищі просторове магнітне поле — магнітний момент μМ [А·м2] електричного струму I [А] навколо елемента поверхні площею dS [м2].

Магнетизм атомів та молекул зумовлений спіновим магнетизмом електронів, їх орбітальними магнітними моментами та власними й орбітальними моментами нуклонів у ядрах. Загальний магнітний момент атома складається із суми магнітних моментів його електронів та ядра. Магнітні властивості нуклонів ядра приблизно в 1000 разів слабші за магнітні властивості електронів, тож, їх магнітні моменти мало впливають на намагнічування матеріалу. Магнітні властивості матеріалу в основному визначаються електронами та їх магнітними моментами.
Магнетизм електрона. Однією з найважливіших властивостей електрона є наявність у нього не лише електричного, але й власного магнітного поля. Власне магнітне поле електрона називають квантово-механічним спіном (англ. spin — обертання). Електрон володіє магнітним дипольним моментом, що витікає із спіну електрона, тож, поводить себе подібно маленькому магніту. Згідно квантової теорії, спін може бути в одному з двох станів: у верхньому (up) або в нижньому (down). Спін електронів є головним джерелом магнетизму.
Електрон створює магнітне поле також за рахунок орбітального руху навколо ядра, який можна вважати круговим мікрострумом.
Магнітні поля, зумовлені спінами електронів та їх орбітальними рухами, визначають широкий спектр магнітних властивостей речовини.
Значна частина електронів у матеріалі розташовані так, що їх орбітальні та внутрішні магнітні моменти один одного скасовують. Певною мірою це можна пояснити поєднанням електронів у пари з протилежними внутрішніми магнітними моментами відповідно до принципу виключення Паулі та утворення заповнених підоболонок з нульовим орбітальним рухом. Непарні електрони чи незаповнені підоболонки атомів, врешті-решт, мають такі розташування, що в сукупності роблять речовину немагнітною. Повний дипольний момент матеріалів з повністю заповненими електронними оболонками дорівнює нулю. Тому магнетизм існує тільки в речовині з частковим заповненням електронних оболонок атомів.
За відсутності зовнішнього магнітного поля молекулярні струми та магнітні моменти окремих молекул в речовині орієнтовані хаотично, тож, сумарний магнітний момент тіла буде дорівнювати нулю, внаслідок чого й результуюче поле дорівнюватиме нулю.
Під дією зовнішнього магнітного поля (В1) магнітні моменти молекул орієнтуються в одному напрямі, й речовина набуває сумарний магнітний момент, відмінний від нуля. Магнітні поля окремих молекулярних струмів вже не компенсують один одного, й виникає власне магнітне поле з вектором магнітної індукції B11. При зміні напряму та/або величини зовнішнього магнітного поля (В2) спостерігається відповідний кутовий дрейф магнітних моментів мікрочастинок, та створюється власне магнітне поле з вектором магнітної індукції B21.
Магнітні властивості матеріалу залежать від його структури, зокрема, від розташування електронів, а також від температури, бо при високій температурі конфігурація електронів руйнується.
Магнітна проникність μ [Гн/м = Н·А–2] – характеристика магнітних властивостей матеріалу, в якому магнітна індукція B [Tл] лінійно залежить від напруженості магнітного поля Н [A/м]. Взаємозв'язок магнітної індукції з вектором напруженості магнітного поля Н [A/м] здійснюється через магнітну проникність μ [Н·А–2],
B = μ·Н.
У порожнечі магнітна проникність вільного простору має величину μ0 = 4·π·10–7 Н·А–2,
B = μ0·H [Tл].
Фізична величина, що показує, в скільки разів індукція магнітного поля в речовині B [Tл] відрізняється по модулю від індукції магнітного поля у вакуумі B0 [Tл], називається відносною магнітною проникністю μr (безрозмірна величина),
μr = B/B 0. {\displaystyle \mu _{r}={\frac {\mu }{\mu _{0}}}.}
Відносна магнітна проникність μr є відношенням проникності певного середовища μ до проникності вільного простору (магнітної константи) μ0,
μr = μ/μ0.
Непостійність магнітної проникності приводить до складної нелінійної залежності індукції B магнітного поля у феромагнетику від індукції B0 зовнішнього магнітного поля.
Магнітне поле в речовині має вигляд
B = μ0·(H + M), де M [A/м] — намагніченість (магнітна поляризація), вектор поля, який визначає густину власних чи наведених магнітних моментів в об'ємі речовини.
Для нескінченно малих величин дипольного моменту m [A·м2] та об'єму речовини V [м3] намагніченість записується так
M = dm/dV.
У інтегральному вигляді магнітна поляризація M [A/м] записується через кінцеві значення дипольного моменту m [A·м2] та об'єму V [м3],
M = m/V.
Магнітна поляризація M та дипольний момент m можуть бути визначена через залишкову густину магнітного потоку Br (англ. magnetic flux density) [Тл],
M = (1/μ0)·Br;
m = (1/μ0)·Br·V.
У речовині магнітна поляризація M [A/м] є лінійною функцією вектора напруженості магнітного поля H [A/м],
M = χV·H,
де χV — об'ємна магнітна сприйнятливість, безрозмірна величина, яка характеризує здатність речовини намагнічуватись під дією зовнішнього магнітного поля.
Об'ємна магнітна сприйнятливість χV пов'язана з магнітною проникністю μ [Н·А–2],
μ = μ0·(1 + χV), де μ0 [Н·А–2] — магнітна проникність вільного простору, μ0 = 4·π·10−7 Н·А−2.
У дослідженнях магнітних властивостей використовують також поняття питомої магнітної сприйнятливості χsp [м3/кг]. Питома магнітна сприйнятливість є об'ємною магнітною сприйнятливістю одиниці маси тіла,
χsp = χV/ρ ,
де ρ [кг/м3] — густина тіла.
Загальний зв'язок між параметрами B, H та M
B = μ0·(H + M) = μ0·(1 + χV)·H = μ0·μr·H = μ·H.
Магнітними властивостями атомів або субатомних частинок (електронів, протонів і нейтронів), що входять до складу атомів, а також характером взаємодії частинок-носіїв магнітного моменту визначаються різні види магнетизму в речовині: діамагнетизм, парамагнетизм та феромагнетизм.
Силова взаємодія магнітного поля з різними речовинами також відбувається по-різному. При поміщенні діамагнетика DM в неоднорідне сильне магнітне поле магніту N-S діамагнетик виштовхуються з області поля силою F. При поміщенні в це магнітне поле парамагнетика РМ він втягується в область поля силою F.
Магнітогідродинаміка рідинного середовища вивчає магнітні властивості рідини і є складовою частиною гідродинаміки. Лінії течії, трубки течії, густина ліній течії рідини не тільки характеризують динаміку руху частинок у просторі та часі магнітогідродинамічних систем, але й тісно пов'язані із силовими лініями зовнішнього магнітного поля. Під впливом магнітного поля в потоці електропровідної рідини виникають електричні струми. Вони поляризують рідину й, в свою чергу, змінюють зовнішнє магнітне поле. Так магнітне поле впливає на потік рідини, а потік рідини впливає на магнітне поле.
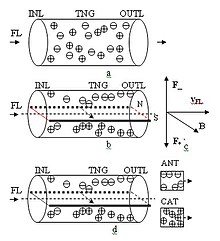
Магнітне поле впливає на потік електроліту FL, який рухається з лінійною швидкістю vFL у флюїдопроводі TNG з вхідним INL та вихідним OUTL отворами. За відсутності зовнішнього магнітного поля йонізовані частинки електроліту розсіяні в потоці випадковим чином. Позитивні та негативні йони розподілені по об'єму потоку рівномірно в межах статистичної похибки, тож, просторової концентрації йонів одного знаку не спостерігається.
При появі зовнішнього магнітного поля, створеного магнітом N-S і показаного вектором магнітної індукції B, на негативні електричні заряди електроліту діє сила Лоренца F–, а на позитивні електричні заряди — сила Лоренца F+. Під впливом діючих сил електроліт, який рухається з лінійною швидкістю vFL, поляризується: негативні йони зміщуються у верхню частину каналу, а позитивні — в нижню. В результаті, на виході OUTL флюїдопроводу частинки електроліту діляться на два потоки й можуть, у разі необхідності, транспортуватися двома окремими каналами — флюїдопроводом аніонів ANT та флюїдопроводом катіонів CAT.
У зовнішньому магнітному полі частинки електроліту створюють динамічні колективи: пучки, струмені, а де й подвійні електричні шари. Текучість та деформація суцільних середовищ, якими є розчини електролітів, досліджуються в рамках гідромеханіки, теорії пружності та пластичності. Зокрема, закон Ньютона використовується для тлумачення в'язкого тертя в рідинах, закон Гука — для визначення залежності між деформаціями та механічними напруженнями в тілі.
При розрахунках МГД-систем використовуються взаємозв'язані рівняння гідродинаміки Нав'є-Стокса, які пояснюють рух нестисливої в'язкої рідини, та рівняння електромагнітного поля Максвелла. Формульні лабіринти створені математиками не для того, щоб задовольнити свою пихатість, математика — це аргументи на захист ідеї.
Для опису потоку рідини в рамках класичної термодинаміки достатньо мати 3 складові вектора швидкості vFL [м/с], густину ρ [кг/м3], тиск p [Па] та температуру T [К]. Швидкість потоку vFL потрібна, зокрема, для того щоб визначити параметри електромагнітного поля із рівнянь Максвела, оскільки вона фігурує у виразі для густини струму J [А/м²]. Питома вага ρ, тиск p та температура T рідини зв'язані між собою загальним рівнянням
f(ρ, p, T) = 0.
Рівняння руху рідини описують збереження маси, моменту та енергії,
∂vFL/∂t + (vFL· )vFL — μK·2vFL = –W + g, де vFL — швидкість рідини, (vFL·)vFL — складова конвекції, — оператор Гамільтона або набла, μK·2vFL — складова дифузії, описується векторним диференціальним оператором Лапласа, (–ÑW) — складова, що враховує внутрішнє джерело енергії, W [Дж] — питома термодинамічна робота, W = (1/ρ0) = (р/ρ0), μK [Ст, м²/с] — кінематична в'язкість, μK = μ/ρ0, μ [Па·с] — динамічна в'язкість, ρFL [кг/м3] — густина рідини, t [с] — час, g — складова, яка відображає зовнішнє джерело енергії.
E + ∂B/∂t = 0;
curl H — ∂D/∂t = J;
div D = ρе;
div B = 0.
Наведені рівняння можна переписати у вигляді
×E + ∂B/∂t = 0;
×H — ∂D/∂t = J;
·D = ρе;
·B = 0.
де E [В/м] — вектор напруженості електричного поля, H [A/м] — вектор напруженості магнітного поля, B [Tл] — магнітна індукція, D [Кл/м²] — електричне зміщення (електрична індукція), J [А/м²] — густина електричного струму; ρе [Кл/м²] — густина заряду, div або (·) — оператор дивергенції, curl або (×) [1/м] — оператор ротора.
У рівняннях використана система одиниць, в якій швидкість світла, електрична та магнітна сталі приймаються рівними одиниці (с = μ0 = ε0 = 1), тож поля мають однакову розмірність.
Фізична суть рівнянь:
- електрична напруга, яка індукується в замкнутому електричному колі, пропорційна швидкості зміни магнітної індукції (закон індукції М. Фарадея), або зміна магнітної індукції породжує вихрове електричне поле;
- циркуляція вектора напруженості магнітного поля по довільному нерухомому контуру в електромагнітному полі дорівнює алгебраїчній сумі макрострумів та струму зміщення через поверхню контуру, або електричний струм та зміна електричної індукції породжують магнітне поле;
- потік електричного зміщення через довільну замкнуту поверхню в електромагнітному полі дорівнює сумарному вільному заряду, який знаходиться всередині області, обмеженої цією поверхнею, або електричний заряд є джерелом електричної індукції;
- магнітний потік через довільну нерухому замкнуту поверхню в електромагнітному полі дорівнює нулю, або не існує магнітних зарядів.
У декартових координатах
div D = ·D = ∂Dx/∂х +∂Dy/∂у + ∂Dz/∂z;
div B = ·B = ∂Bx/∂х +∂By/∂у + ∂Bz/∂z,
де – оператор Гамільтона, = (∂ /∂х; ∂ /∂у; ∂ /∂z).
Математичні перетворення дозволяють отримати корисні для розрахунків співвідношення
D = ε0·E;
B = μ0·H;
J = jcv + jcd;
J = χEL·(E + v×B), де J [А/м²] — густина електричного струму, ε0 — електрична проникність вакууму, μ0 [Н/А²] — магнітна проникність вакууму, χEL [См/м] — питома електрична провідність, jcv [А/м²] — густина конвекційного струму, зумовленого рухом наелектризованих тіл, наприклад, мікрочастинок, jcd [А/м²] — густина струму провідності.
Електромагнітне поле володіє енергією, яка може бути визначена на одиницю об'єму через густину енергії UEM,
UEM = (1/2)·E·D + (1/2)·B·H = (ε0/2)·E2 + [1/(2·μ0)]·B2,
де ε0 та μ0 — електрична та магнітна проникності вакууму.
При розв'язанні рівнянь Нав'є–Стокса і Максвелла вводяться деякі спрощення:
- струм зміщення настільки малий, що їм можна знехтувати (∂D/∂t = 0);
- конвекційний струм значно менший, ніж струм провідності, J = Jcd = χEL·(E+v×B);
- при надплинності рідини divD = ρе = 0, тож, приймаємо curl H = jcd.
Електромагнітна енергія UEM зводиться до магнітної енергії UM,
UM = [1/(2·μ0)]·B2.
Пояснити роботу МГД-генератора допомагає закон електромагнітної сили Лоренца. На заряджену частинку, яка рухається з електролітом в електромагнітному полі перпендикулярно його лініям напруженості, діє сила F [Н]. У разі, коли магнітне поле діє, а електричне поле відсутнє,
F = q·(vFL×B), де q [Кл] — заряд частинки, vFL [м/с] — швидкість частинки, B [Тл] — вектор магнітної індукції.
У разі, коли діють магнітне й електричне поля,
F = q·(E + vFL×B).
Сила Лоренца F [Н] протидіє руху частинки. Згідно закону Фарадея, в провіднику, який находиться в електромагнітному полі, виникає електрорушійна сила. У напрямку, перпендикулярному напряму руху рідини та напряму вектора магнітної індукції, електрорушійна сила створює електричний струм.
Силу Лоренца можна виразити через струми,
F = ρe·E + j×B.
Кінетична енергія руху розчину електроліту йде на подолання сили магнітної індукції FIND [Н].
Рівняння Нав'є-Стокса та Максвелла є прикладом того, як аргументи математики допомагають реалізувати ймовірне.

Базові структурна та конструктивна схеми рідинної магнітогідродинамічної системи формування електричного струму включають потік рідинного електроліту FL з йонізованими частинками та сумарного магнітних полів відповідно; RL — електричний навантажувальний опір; I — електричний струм (EC); EN — електрична мережа.
Вироблення електричної енергії відбувається так. Під час руху електролітичного розчину FL з лінійною швидкістю vFL в силовому магнітному полі магніту N-S з вектором магнітної індукції В1 йони електроліту під дією сили Лоренца F– (на негативні електричні заряди) і F+ (на позитивні електричні заряди) відхиляються та створюють колективне динамічне магнітне поле, яке характеризується вектором магнітної індукції В3. За цих умов колективне магнітне поле зарядів взаємодіє із зовнішнім силовим полем та створює в оточуючому середовищі сумарне магнітне поле, позначене вектором магнітної індукції В2. Змінне магнітне поле індукує у влаштованих провідниках-електродах ELS(–) та ELS(+) електрорушійну силу, яка викликає в замкнутому колі постійний електричний струм I. В електричному адаптері EA цей електричний струм перетворюється в змінний. Сила струму, електрична напруга та частота доводяться до значень, придатних для споживання, після цього струм спрямовується споживачам та/або в електричну мережу EN.
Ускладнюючим фактором магнітогідродинамічного генератора є поява ефекту Холла внаслідок вищої рухомості електронів у плазмі порівняно з йонами. Ефект Холла можна також посилити та покласти в основу роботи магнітогідродинамічного генератора.
Перспективними для дослідження є офшорні магнітогідродинамічні системи, для яких природним розчином електроліту є морська солона вода, а моря та океани є натуральними резервуарами цього розчину. Джерелом механічної відновлюваної енергії в офшорних системах служать океанічні течії, припливи гравітаційного походження та хвилі. У деяких системах рушієм електроліту є міжмолекулярні сили адгезії та поверхневого натягу.
Аксіальна сила Лоренца, яка діє на одиницю об'єму електроліту, пропорційна густині струму J [A/м2], індукції магнітного поля B [Тл] та тиску p [Па], Fy = –|J×B| = –J·B = dp/dy [Н/м3].
Негативний знак у рівнянні свідчить про те, що магнітна сила спрямована проти потоку електроліту. У результаті, dp/dy < 0, із зростанням у тиск падає. При використанні сегментованих електродів осьовий струм в каналі відсутній (Jy = 0), тож J = Jx [A/м2], J = –χEL·(vFL·B — Ex).
За умов розімкнутого кола J = 0 останнє рівняння перетворюється в таке
Ex-OP = vFL·B [В/м].
У разі замкнутого електричного кола числове значення вектора напруженості електричного поля Ex [В/м] визначається коефіцієнтом навантаження каналу K — відношенням величини внутрішнього опору генератора RG до величини зовнішнього електричного навантажувального опору RL,
Ex = K·vFL·B.
Значення коефіцієнта навантаження находиться в межах 0 ≤ K ≤ 1. Густина струму J [A/м2] вираховується так
J = χEL·vFL·B·(1 — K).
Питома потужність електричного струму P1EL-OUT [Вт/м3], який протікає через навантажувальний опір, на одиницю об'єму каналу 1 м3 визначається як добуток скалярних величин, P1EL-OUT = | J·E | = χEL·vFL2·B2·K·(1 — K).
Зі зростанням об'єму V [м3] МГД-каналу потужність електричного струму пропорційно зростає. Повна потужність каналу PEL-OUT [Вт] складає
PEL-OUT = χEL·vFL2·B2·K·(1 — K)·V.
Тож, електрична потужність МГД-генератора пропорційна квадрату швидкості електролітичного розчину vFL2, квадрату магнітної індукції В2 а також об'єму каналу V [м3]. Для отримання великих потужностей потрібно розганяти розчин електроліту до великих швидкостей та одночасно забезпечувати його високу електропровідність χEL [Ом−1·м−1].
Сила гальмування Fy [Н] на одиницю об'єму 1 м3 находиться як добуток скалярних величин J [А/м2] та B [Тл], Fy = –J·B = –χEL·vFL·B2·(1 — K) [Н/м3].
Потужність P1IN [Вт/м3] сили Fy, яка рухає рідину в каналі на одиницю об'єму 1 м3, дорівнює
P1IN = Fy·vFL = χEL·vFL2·B2·(1 — K) [Вт/м3].
Джоулеві втрати I2R потужності можна знайти як різницю між потужністю, яка потрібна для руху рідини PIN, та корисною потужністю струму PEL-OUT, що протікає через зовнішній навантажувальний опір, χEL·vFL2·B2·(1 — K) — χEL·vFL2·B2·K·(1 — K)
J2/χEL = [χEL·vFL·B·(1 — K)]2/χEL = χEL·(vFL·B)2·(1 — 2K + K2) =
= χEL·vFL2·B2·(1 — K) — χEL·vFL2·B2·K·(1 — K) =
= χEL·vFL2·B2·(1 — K)2 [Вт/м3].
Коефіцієнт корисної дії k каналу вираховується як відношення вихідної потужності PEL-OUT до вхідної PIN,
k = PEL-OUT/PIN = K.
При K = 1 потужність падає до нуля. Максимальне значення потужності спостерігається при K = 0,5.
Ефект Холла, характерний для схеми МГД-генератора Фарадея, знижує густину електричного струму J [А/м2], J = [χEL/(1 + βH2)]·(vFL·B — Е), де βH — коефіцієнт Холла, для рідинного електроліту визначається як відношення між частотою обертання електрона ω [с−1] та частотою співударів з йонами (1/τ) [с−1],
βH = ω·τ = Ey/(Bz·Jx).
Відповідно знижується й питома вихідна електрична потужність P1EL-OUT [Вт/м3] струму, який проходить через навантажувальний опір на одиницю об'єму каналу 1 м3,
P1EL-OUT = J·E = [χEL/(1 + βH2)]·vFL2·B2·K·(1 — K) [Вт/м3].
З іншого боку, повна вихідна електрична потужність PEL-OUT струму, який проходить через навантажувальний опір, зростає пропорційно об'єму V [м3] МГД-каналу, PEL-OUT = J·E = [χEL/(1 + βH2)]·vFL2·B2·K·(1 — K)·V [Вт].
Кількість електроенергії ЕHPP-EL, яка може бути вироблена за певний час роботи системи, наприклад, продовж року, дорівнює добутку її електричної потужності PEL-OUT [Вт] на час роботи t [с], ЕEL = PEL-OUT ·t = χEL·vFL2·B2·K·(1 — K)·V·t [кВт·год].
Вартість електричної енергії PPRΣ [US$], яка може бути вироблена за певний період роботи системи, наприклад, продовж року, дорівнює добутку ціни одиниці електричної енергії pPR [US$/кВт·год] на кількість енергії ЕEL [кВт·год], PPRΣ = pPR·ЕEL = pPR·χEL·vFL2·B2·K·(1 — K)·V·t [US$].
Кількість органічного викопного палива, наприклад, об'єм VOFF [м3] природного газу з питомою теплотворною здатністю сOFF [Дж/м3], яке заощаджується при функціонуванні молекулярної магнітогідродинамічної електростанції продовж року, розраховується так
VOFF = ЕEL/(kOFF·сOFF) =
= χEL·vFL2·B2·K·(1 — K)·V·t/(kOFF·сOFF), де kOFF — коефіцієнт корисної дії теплоенергетичних систем на органічному паливі, в енергоефективних системах kOFF ≈ 0,4.
Нижче наведені енергетичні та економічні параметри магнітогідродинамічного генератора, розраховані для величини магнітної індукції В = 5 Тл та різних значень швидкості електролітичного розчину: vFL1 = 2 м/с; vFL2 = 4 м/с; vFL3 = 6 м/с; vFL4 = 8 м/с; vFL5 = 10 м/с. Використані такі значення інших параметрів: об'єм МГД-каналу V = 1 м3; електропровідність морської води χEL = 4,8 (Ом·м)−1; коефіцієнт навантаження К = 0,6; ціна одиниці електричної енергії pPR = 0,1 US$/кВт·год; питома теплотворна здатність природного газу сOFF = 32,7 МДж/м3.
Параметри МГД-генератора малої потужності
| Найменування параметра | Значення параметра | ||||
| Швидкість розчину електроліту, м/с | 2 | 4 | 6 | 8 | 10 |
| Потужність PEL-OUT, кВт | 0,115 | 0,46 | 1,04 | 1,84 | 2,88 |
| Е-енергія за 1 рік ·103, кВт·год | 1,0 | 4,0 | 9,87 | 16,1 | 25,2 |
| Вартість е/енергії за 1 рік·103, US$ | 0,1 | 0,4 | 0,99 | 1,61 | 2,52 |
| Кількість заощадженого п/газу за 1 рік ·103, м3 | 0,28 | 1,1 | 2,51 | 4,44 | 6,94 |
- Сидоров, В. І. (2020). Молекулярна енергетика. Теорія та технічні рішення. (Укр.). Черкаси: Вертикаль, видавець Кандич С. Г. с. 486 с. ISBN 978-617-7475-79-7.
- Faraday, M. Experimental Researches in Electricity. First Series // Philosophical Transactions of the Royal Society. — 1832. Р. 125162.
- Alfven, H. Existance of electromagnatic-hydrodynamic waves // Nature. — 1942. — Vol. 150, Iss. 3805. — P. 405—406.
- Alfven, H. On the cosmogony of the solar system III // Stockholms Observatoriums Annaler. — Vol. 14. — Р. 1-9.
- Maxwell, J. C. A Dynamical Theory of the Electromagnetic Field // Phil. Trans. R. Soc. Lond. — 1865. –Vol. 155. — Р. 459—512.
- Heisenberg, W. Zur Theorie des Ferromagnetismus (On the theory of ferromagnetism) // Zeitschrift für Physik. — 1928. — Vol. 49, № 9-10. — P. 619—636.
- Dirac, P. A. M. The Quantum Theory of the Electron // Proceedings of the Royal Society of London. — 1928. — 117 (778). — P. 610—624
- Dirac, P. A. M. (). On the Theory of Quantum Mechanics // Proceedings of the Royal Society. — 1926. — 112 (762). — P. 661—677.
- Dirac, P. A. M. The Principles of Quantum Mechanics. Oxford, Clarendon Press, 1930.
- Dirac, P. A. M. Lectures on quantum mechanics. 1931
- Lundquist, S. Experimental investigations of magneto-hydrodynamic waves // Physical Review. — 1949. — Vol. 76. — Р. 1805—1809.
- Sutton, G. W. and Sherman, A. Engineering Magnetohydrodynamics. — New York: MacGraw-Hill, 1965. — 548 p.
- Hughes, W. F. and Young, F. J. The Electromagnet dynamics of fluids. — New York: John Wiley and Sons, 1966.
- Elliott, D. G. Direct current liquid-metal magnetohydrodynamic power generation // AIAA Journal. — 1966. — Vol. 4, № 4. — Р. 627—634.
- Rosa, R. J. Magnetohydrodynamic energy conversion. — Washington: Hemisphere Pub. Corp., 1987.
- Ozawa, Y., Kayukawa, N. Effect of Magnetic Field Upon the Output Characteristics of an Open-Type Faraday MHD Power Generator. 14th Syrnp. on Engineering Aspects of MHD, Tullahoma, USA, April 1974.
- Yoshizawa, A. Hydrodynamic and Magnetohydrodynamic Turbulent Flows. Modelling and Statistical Theory. — Publisher, Springer Netherlands, 1998.
- Takeda, M. et al. Fundamental Studies on Helical-Type Seawater MHD Generation System // IEEE Transactions on Applied Superconductivity. — 2005. — Vol. 15, № 2. — Р. 2170—2173.
- Takeda, M., Hirosaki, H., Kiyoshi, T., Nishio, S. Fundamental Study of Helical-Type Seawater MHD Power Generation with Partitioned Electrodes // Journal of the JIME. — 2014. — Vol. 49, № 3. — Р. 113—117.
- Morgan, E. R. and Shafer M. W. Marine Energy Harvesting Using Magnetohydrodynamic Power Generation. — ASME 2014 Conference on Smart Materials, Adaptive Structures and Intelligent Systems. Volume 2: Mechanics and Behavior of Active Materials; Integrated System Design and Implementation; Bioinspired Smart Materials and Systems; Energy Harvesting Newport, Rhode Island, USA, September 8-10, 2014.
- Stuetzer, O. M. Magnetohydrodynamics and electrohydrodynamics // Phys. Fluids. — 1962. — Vol. 162. № 5. — Р. 534—544.
- Dulikravich, G. S. and Lynn, S. R. Unified electro-magneto- fluid dynamics (EMED): introductory concepts // Int. J. Non-Linear Mechanics. — 1997. — Vol. 32. — Р. 913—922.
- ↑ Сидоров, В.І. (2020). Молекулярна енергетика. Теорія та технічні рішення (Укр.) . Черкаси: Вертикаль, видавець Кандич С.Г. с. 486. ISBN ISBN 978-617-7475-79-7..
{{cite book}}: Перевірте значення|isbn=: недійсний символ (довідка) - ↑ Alfven, H. (1942). Existence of electromagnetic-hydrodynamic waves. Nature. – Vol. 150, Iss. 3805. – Р. 405-406 (Англ.) .
{{cite news}}:|access-date=вимагає|url=(довідка) - ↑ Alfven, H. (1942). On the cosmogony of the solar system. Stockholms Observatoriums Annaler. - Vol. 14. – Р. 1-9 (Англ.) .
{{cite news}}:|access-date=вимагає|url=(довідка) - ↑ Lundquist, S. (1949). Experimental investigations of magneto-hydrodynamic waves. Physical Review. – Vol. 76. – Р. 1805-1809 (Англ.) .
{{cite news}}:|access-date=вимагає|url=(довідка) - ↑ Sutton, G. W. and Sherman, A. (1965). Engineering Magnetohydrodynamics (Англ.) . New York: MacGraw-Hill,. с. 548.
- ↑ Hughes, W. F. and Young, F. J. (1966). The Electromagnet dynamics of fluids. New York: John Wiley and Sons.
- ↑ Elliott, D. G. (1966). Direct current liquid-metal magnetohydrodynamic power generation. AIAA Journal. – Vol. 4, № 4. – Р. 627-634 (Англ.) .
{{cite news}}:|access-date=вимагає|url=(довідка)


 French
French Deutsch
Deutsch