五維正六胞體 - 维基百科，自由的百科全书

五维正六胞体 （6-超胞） 5-体
類型	凸五维正多胞体
家族	单纯形
維度	5
對偶多胞形	自身对偶
類比	正四面體
數學表示法
考克斯特符號 （英语：Coxeter-Dynkin diagram）
施萊夫利符號	{3,3,3,3} {3,3,3}x{} {3,3}x{1} {3,3}x{}x{} {3}x{3}x{} {3}x{}x{}x{} {}x{}x{}x{}x{}
性質
四维胞	6 {4,3,3}
胞	15 (3.3.3)
面	20 {3}
邊	15
頂點	6
特殊面或截面
皮特里多边形	六邊形
組成與佈局
顶点图	正五胞体
對稱性
對稱群	BC5, [3,3,3,3]
特性
凸
查 论 编

五维正六胞体（Hexateron）或称正六超胞体（Hexateron）是3个五维凸正多超胞体之一，一種自身對偶的五維多胞體，是五维的单纯形，四维正五胞体、三维正四面体、二维正三角形的五维类比。由6个正五胞体胞、15个正四面体胞、20个正三角形面、15条棱、6个顶点组成。它的二超胞角是cos⁻¹(¹/₅)，约等于78.46°。正如其它维的正单纯形一样，正六超胞体可以被看作是正五胞体的棱锥，即正五胞体棱锥，它由一个正五胞体底面一个与正五胞体5个顶点距离都相等且等于正五胞体棱长的顶点相连而成，正五胞体的正四面体胞与顶点相连成为5个正四面体棱锥（即正五胞体）侧面。

正六超胞体的顶点处有5条棱相交，应此它的顶点图是正五胞体，在它的棱处有4个正五胞体维脊相交，应此它的棱图是正四面体。它有施莱夫利符号{3,3,3,3}，考斯特-迪肯符号，它像其它正单纯形一样是自身对偶的。 对于一个边长为a的正六超胞体，其超胞积是${\displaystyle {\cfrac {{\sqrt {3}}a^{5}}{480}}}$,表胞积是${\displaystyle {\cfrac {{\sqrt {5}}a^{4}}{16}}}$,高是${\displaystyle {\cfrac {{\sqrt {30}}a}{5}}}$。 若一个正六超胞体的棱长为1，则其外接五維超球的半径为${\displaystyle {\frac {\sqrt {15}}{6}}}$,內切五維超球的半径为${\displaystyle {\frac {\sqrt {15}}{30}}}$。

为了得到正六超胞体的顶点坐标，我们可以将其看作是由正五胞体和一个与正五胞体5个顶点距离都相等且等于正五胞体棱长的顶点相连而成。经过计算之后，我们便可将棱长为2，中心在五维直角坐标系原点的正六超胞体顶点坐标表示为：

${\displaystyle \left({\sqrt {\frac {1}{15}}},\ {\sqrt {\frac {1}{10}}},\ {\sqrt {\frac {1}{6}}},\ {\sqrt {\frac {1}{3}}},\ \pm 1\right)}$

${\displaystyle \left({\sqrt {\frac {1}{15}}},\ {\sqrt {\frac {1}{10}}},\ {\sqrt {\frac {1}{6}}},\ -2{\sqrt {\frac {1}{3}}},\ 0\right)}$

${\displaystyle \left({\sqrt {\frac {1}{15}}},\ {\sqrt {\frac {1}{10}}},\ -{\sqrt {\frac {3}{2}}},\ 0,\ 0\right)}$

${\displaystyle \left({\sqrt {\frac {1}{15}}},\ -2{\sqrt {\frac {2}{5}}},\ 0,\ 0,\ 0\right)}$

${\displaystyle \left(-{\sqrt {\frac {5}{3}}},\ 0,\ 0,\ 0,\ 0\right)}$

如果我们将正六超胞体当作是位于六维直角坐标系中的超平面，则正六超胞体的顶点坐标可以简单地表示为(0,0,0,0,0,1)或者(0,1,1,1,1,1)的全排列，这样的正六超胞体实则是六维正轴体（前者）或者截半六维超正方体（后者）的一个表面。

作为五维的正单纯形，一个五维凸正多超胞体，它具有A₅考克斯特平面对应的对称群构造，对应施莱夫利符号{3,3,3,3}，考斯特-迪肯符号。同时，它可被看作是四维正五胞体的棱锥，只具有A₄对应对称性。

五维正六胞体可以以自身的对称性被平行投影到2维平面上：

正交投影

Ak 考克斯特平面（英语：Coxeter plane）	A5	A4
图像
二面体对称群	[6]	[5]
Ak 考克斯特平面（英语：Coxeter plane）	A3	A2
图像
二面体对称群	[4]	[3]

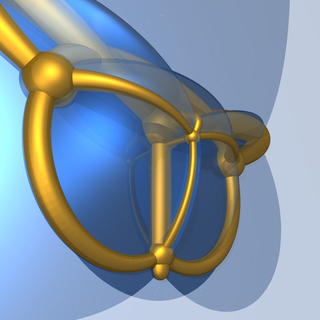正六超胞体的五维到四维施莱格尔图像（英语：Schlegel diagram）的四维到三维球极投影的三维到二维透视投影。

• 正五胞体
• 五维空间
• 五维超正方体
• 五维正轴体

• T. Gosset：On the Regular and Semi-Regular Figures in Space of n Dimensions，Messenger of Mathematics，Macmillan，1900
• H.S.M.考克斯特：
  • 考克斯特，Regular Polytopes，(第三版，1973)，Dover edition，ISBN 0-486-61480-8，p.296，Table I (iii)：Regular Polytopes, three regular polytopes in n-dimensions (n≥5)
  • H.S.M.考克斯特，Regular Polytopes，第三版，Dover New York，1973，p.296，Table I (iii)：Regular Polytopes，three regular polytopes in n-dimensions (n≥5)
  • Kaleidoscopes: Selected Writings of H.S.M. Coxeter，editied by F. Arthur Sherk，Peter McMullen，Anthony C. Thompson，Asia Ivic Weiss，Wiley-Interscience Publication，1995，ISBN 978-0-471-01003-6 [1]（页面存档备份，存于互联网档案馆）
    • (第22页) H.S.M. Coxeter, Regular and Semi Regular Polytopes I, [Math. Zeit. 46 (1940) 380-407, MR 2,10]
    • (第23页) H.S.M. Coxeter, Regular and Semi-Regular Polytopes II, [Math. Zeit. 188 (1985) 559-591]
    • (第24页) H.S.M. Coxeter, Regular and Semi-Regular Polytopes III, [Math. Zeit. 200 (1988) 3-45]
• John H. Conway，Heidi Burgiel，Chaim Goodman-Strass，The Symmetries of Things 2008，ISBN 978-1-56881-220-5 (Chapter 26. pp. 409: Hemicubes: 1_n1)
• 诺曼·约翰逊（英语：Norman Johnson (mathematician)） Uniform Polytopes，Manuscript (1991)
  • N.W.约翰逊: The Theory of Uniform Polytopes and Honeycombs，Ph.D. (1966)
• Klitzing, Richard. 5D uniform polytopes (polytera) x3o3o3o3o - hix. bendwavy.org.