星形截角立方体 - 维基百科,自由的百科全书
 | |||
| 類別 | 均匀星形多面體 | ||
|---|---|---|---|
| 對偶多面體 | 大三角化八面體 | ||
| 識別 | |||
| 名稱 | 星形截角立方体 | ||
| 參考索引 | U19, C66, W92 | ||
| 鮑爾斯縮寫 | quith | ||
| 數學表示法 | |||
| 考克斯特符號 | |||
| 施萊夫利符號 | t{4/3,3} | ||
| 威佐夫符號 | 2 3 | 4/3 2 3/2 | 4/3 | ||
| 性質 | |||
| 面 | 14 | ||
| 邊 | 36 | ||
| 頂點 | 24 | ||
| 歐拉特徵數 | F=14, E=36, V=24 (χ=2) | ||
| 組成與佈局 | |||
| 面的種類 | 8個三角形{3} 6個八角星{8/3} | ||
| 面的佈局 | 8{3}+6{8/3} | ||
| 頂點圖 | 3.8/3.8/3 | ||
| 對稱性 | |||
| 對稱群 | Oh, [4,3], *432 | ||
| 特性 | |||
| 非凸、半正、點可遞 | |||
| 圖像 | |||
| |||
在幾何學中,星形截角立方體是一種鳶形二十四面體的星形多面體,由互相相交的三角形和八角星組成,其索引為U19,對偶多面體是大三角化八面體[1]。
性質
[编辑]星形截角立方體共有14個面、36條邊和24個頂點[2],在14個面中,有8個正三角形和6個八角星,且每個頂點都是2個八角星和1個三角形的公共頂點,頂點圖可以用8/3.8/3.3表示[3]。在施萊夫利符號中計為 t{4/3,3},其代表著經過截角變換的圖形。考克斯特記號中可以用![]()
![]()
![]()
![]()
![]()
![]()
![]() 表示。
表示。
結構
[编辑]星形截角立方體的結構可以視為立方體透過一種名為「星形截角」的多面體變換構造[4][5]。
將立方體截角變換,截到截面交會後繼續截,但將交會的部分切去,並反向延長,然後持續截更深並延長直到延長的面也交會,並繼續截更深同時也繼續增加延長的面,直到延長的面交錯並凸出。
 |  |  |  |
 |  |  |  |
 |  |  |  |
其也可以視為在立方體的正方形面角落擺上直角三角錐,因此每個頂點旁都會被擺上三個直角三角錐[5]。
 |  |  |
二面角
[编辑]星形截角立方體有兩種二面角,包括了八角星-三角形二面角和八角星-八角星二面角。其中八角星-八角星二面角為直角;八角星-三角形二面角為三的平方根倒數之反餘弦值[6]:
尺寸
[编辑]體積與表面積為:[7]
頂點座標
[编辑]正交投影
[编辑]| 建立於 | 八角星面 | 正三角形面 | 八角星-八角星 交棱 |
|---|---|---|---|
| 圖像 | 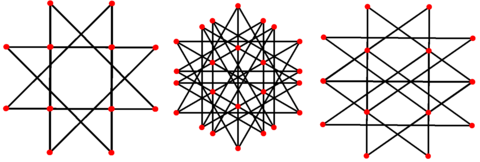 | ||
相關多面體
[编辑]星形截角立方體與另外三種多面體有著相同的頂點布局,他們分別為小斜方截半立方體、小立方立方八面體和小斜方立方體。
 小斜方截半立方體 |  小立方立方八面體 |  小斜方立方體 |  星形截角立方體 |
對偶複合體
[编辑]星形截角立方體與其對偶的複合體為複合星形截角立方體大三角化八面體。其共有38個面、72條邊和38個頂點,其尤拉示性數為4,虧格為-1,有6個非凸面[9]。
參見
[编辑]參考文獻
[编辑]- ^ Eric W. Weisstein. Great Triakis Octahedron, The Dual of the Stellated Truncated Hexahedron.. 密西根州立大學圖書館. (原始内容存档于2016-03-19).
- ^ stellated truncated hexahedron. bulatov.org. (原始内容存档于2016-03-26).
- ^ Uniform Polyhedra 19: stellated truncated hexahedron. mathconsult. (原始内容存档于2016-03-27).
- ^ Truncation. [2017-03-24]. (原始内容存档于2019-04-14).
- ^ 5.0 5.1 Stellated Truncated Hexahedron. software3d.com. [2017-03-24]. (原始内容存档于2019-10-28).
- ^ 6.0 6.1 Self-Intersecting Truncated Regular Polyhedra: Stellated Truncated Hexahedron. dmccooey.com. (原始内容存档于2016-03-24).
- ^ Klitzing, Richard. quasitruncated hexahedron : quith. bendwavy.org. [2021-09-05].
- ^ Data of Stellated Truncated Hexahedron. dmccooey.com. (原始内容存档于2016-09-01).
- ^ compound of stellated truncated hexahedron and great triakisoctahedron. bulatov.org. (原始内容存档于2016-09-06).


 French
French Deutsch
Deutsch










