等轴测投影 - 维基百科,自由的百科全书
此條目翻譯品質不佳。 |

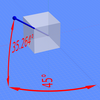
黑色尺寸是三维图形的實際尺寸
紅色尺寸等轴测投影出的尺寸
等轴测投影(Isometric projection)又稱等角投影是技术制图和工程制图中,一種在二維平面呈現三維物體的方法,屬於軸測投影的一種,三條坐標軸的投影缩放比例相同,並且任意兩條坐標軸投影之間的角度都是120度。
概述
[编辑]等轴测投影图可通过使各坐標軸的投影之間角度相等(120°)的視角来获得。以立方體為例,先從一个面正视观察,然後将立方体绕纵轴旋轉±45°,接著将立方体绕横轴旋轉約±35.264° (準確值为 arcsin 1⁄√3或arctan 1⁄√2)。立方體的等轴测投影图(右圖左上)是正六边形:所有黑線長度相等,每个面的投影面積相同。利用等轴测格紙可以无需計算而绘制等轴测投影图。
等轴测投影的视角可以看成是從立方體的頂點看向對面頂點,则x軸为立方體右侧面右下延伸对角线、y軸为左侧面左下延伸对角线、z軸为顶面向上延伸对角线。从此视角投影,各坐标軸的投影彼此成120°。
數學
[编辑]根据觀察卦限的不同,有8種不同的等轴测投影视角。以第一卦限為例,三維上的點ax,y,z等轴测投影到二維上成點 bx,y,數學上可以寫成旋轉矩陣:
其中 α = arcsin(1⁄√3) ≈ 35.264° 且 β = 45°。
接著正投影到xy平面:
另外7種符合等轴测投影視角,可以藉由反方向旋轉或鏡像來達成。[1]
歷史與局限
[编辑]等轴测投影的概念以经验形式存在了數個世紀,然后由William Farish(1759–1837)在1822年首次正式描述。[2][3] 十九世紀中期,等轴测投影成為工程師的重要工具,不久之後等轴测投影和軸測投影进入歐美國家的建築學課程中。[4] 然而,有观点认为軸測投影發源於中國,在中國藝術中起的作用,就如同透視投影之於西洋藝術,随着视觉计算的出现,軸測投影和相關繪圖法則對電腦圖學 亦有所幫助。[5]
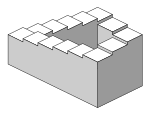
如同各種平行投影方法,等轴测投影繪製的物體不會因為物體距离观察者的遠近而改變大小。雖然有利于建築圖直接測量長度,但卻會造成視覺失真,不像透視投影这种人类视觉和摄像使用的成像方式。等轴测投影有時會造成高度難以辨識(如右左下圖)。這点可被用來創造谬图,如无限循环阶梯。
在视频游戏和像素畫上的用途
[编辑]二十世纪八九十年代,受限于當時的微電腦计算能力,等轴测投影能提供有限的3D效果,因而被用于视频游戏中,例如當時的機台遊戲《立體空戰》。
參見
[编辑]注釋與參考
[编辑]- ^ Ingrid Carlbom, Joseph Paciorek , Dan Lim. Planar Geometric Projections and Viewing Transformations. ACM Computing Surveys (ACM). December 1978, 10 (4): 465–502. doi:10.1145/356744.356750.
- ^ Barclay G. Jones (1986). Protecting historic architecture and museum collections from natural disasters. University of Michigan. ISBN 0-409-90035-4. p.243.
- ^ Charles Edmund Moorhouse (1974). Visual messages: graphic communication for senior students.
- ^ J. Krikke (1996). "A Chinese perspective for cyberspace? (页面存档备份,存于互联网档案馆)". In: International Institute for Asian Studies Newsletter, 9, Summer 1996.
- ^ Jan Krikke (2000). "Axonometry: a matter of perspective". In: Computer Graphics and Applications, IEEE Jul/Aug 2000. Vol 20 (4), pp. 7–11.


 French
French Deutsch
Deutsch