File:Inclinedthrow.gif - 维基百科,自由的百科全书
Inclinedthrow.gif (400 × 288像素,文件大小:374 KB,MIME类型:image/gif、循环、102帧、10秒)
文件历史
点击某个日期/时间查看对应时刻的文件。
| 日期/时间 | 缩略图 | 大小 | 用户 | 备注 | |
|---|---|---|---|---|---|
| 当前 | 2020年10月21日 (三) 16:10 |  | 400 × 288(374 KB) | Geek3 | adjusted friction coefficients such to make terminal velocity of both trajectories equal. In this case, the Newton projectile moves further. |
| 2009年10月21日 (三) 12:57 |  | 400 × 288(453 KB) | AllenMcC. | added Newton drag | |
| 2008年12月22日 (一) 00:40 | 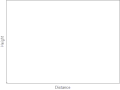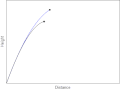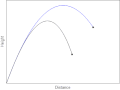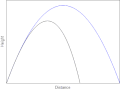 | 400 × 299(393 KB) | AllenMcC. | == Summary == {{Information |Description={{en|1=Trajectories of two objects thrown at the same angle. The blue object doesn't experience any drag and moves along a parabola. The black object experiences Stokes' drag.}} |Source=Own work by uploader |Author | |
| 2008年12月18日 (四) 20:12 |  | 400 × 299(393 KB) | AllenMcC. | == Summary == {{Information |Description={{en|1=Trajectories of two objects thrown at the same angle. The blue object doesn't experience any drag and moves along a parabola. The black object experiences Stokes' drag.}} |Source=Own work by uploader |Author | |
| 2008年12月15日 (一) 04:07 |  | 700 × 519(636 KB) | AllenMcC. | {{Information |Description={{en|1=Trajectories of two objects thrown at the same angle. The blue object doesn't experience friction and moves along a parabola. The black object experiences Stokes friction.}} |Source=Own work by uploader |Author=[[User:All |
文件用途
以下3个页面使用本文件:
全域文件用途
以下其他wiki使用此文件:
- af.wikipedia.org上的用途
- ar.wikipedia.org上的用途
- be.wikipedia.org上的用途
- bg.wikipedia.org上的用途
- bn.wikipedia.org上的用途
- bs.wikipedia.org上的用途
- ca.wikipedia.org上的用途
- cv.wikipedia.org上的用途
- da.wikipedia.org上的用途
- de.wikipedia.org上的用途
- el.wikipedia.org上的用途
- en.wikipedia.org上的用途
- Wave–particle duality
- Trajectory
- Ballistics
- Drag (physics)
- Talk:Field line
- Wikipedia talk:Requests for arbitration/Tang Dynasty
- Wikipedia:Requests for arbitration/Tang Dynasty/Workshop
- User:Enkyo2/Sandbox-L
- Talk:Senkaku Islands/Archive 5
- Bouncing ball
- Wikipedia:Arbitration/Requests/Clarification and Amendment/Archive 34
- User:Eelaraa/Drag (physics)
- eo.wikipedia.org上的用途
- es.wikipedia.org上的用途
- eu.wikipedia.org上的用途
- fa.wikipedia.org上的用途
- fi.wikipedia.org上的用途
- ga.wikipedia.org上的用途
- he.wikipedia.org上的用途
- hi.wikipedia.org上的用途
- hr.wikipedia.org上的用途
- ht.wikipedia.org上的用途
- hu.wikipedia.org上的用途
- hy.wikipedia.org上的用途
查看此文件的更多全域用途。


 French
French Deutsch
Deutsch
