Epiciclo , la enciclopedia libre



El epiciclo (del griego, epi, sobre, y kyklos, círculo, que significa sobre el círculo) fue la base de un modelo geométrico ideado por los antiguos griegos para explicar las variaciones en la velocidad y en la dirección del movimiento aparente de la Luna, el Sol y los planetas. Lo propuso por primera vez Apolonio de Perga a finales del siglo III a. C. y lo usó ampliamente en el siglo II a. C. Hiparco de Nicea. Casi tres siglos después, el también astrónomo griego Claudio Ptolomeo se basó en él para elaborar su versión de la teoría geocéntrica conocida ahora como sistema ptolemaico.
Cuando se registran los movimientos de los planetas todas la noches durante años se obtiene un patrón: el planeta se mueve por el cielo en una dirección, después retrocede en la dirección opuesta y finalmente vuelve a moverse en la dirección original. En el modelo geocéntrico estos datos implican que el planeta se mueve en círculos además de orbitar la Tierra y los datos suponen que cada planeta tiene diferentes velocidades y diámetros en sus epiciclos respectivos.
Con la teoría heliocéntrica de Nicolás Copérnico y la explicación del movimiento planetario en órbitas elípticas por Johannes Kepler, el modelo de los epiciclos quedó obsoleto.
Introducción
[editar]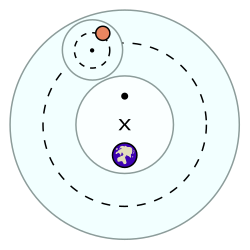
* El centro del deferente es X, pero el movimiento angular del epiciclo es aparentemente acorde solo respecto al punto (·) que es el ecuante.
* El deferente es el recorrido circular que describe el centro del epiciclo.
* El ecuante es el punto en torno al cual se mueve el planeta en su trayectoria, aparentemente.
En ambos sistemas hiparquiano y ptolemaico, se supone que los planetas se mueven en un círculo pequeño llamado epiciclo que, a su vez, se mueve a lo largo de un círculo más grande llamado deferente. Ambos círculos giran en el sentido de las manecillas del reloj y son más o menos paralelos al plano de la órbita del Sol (eclíptica). A pesar de que el sistema se consideraba geocéntrico, el movimiento de los planetas no estaba centrado en la Tierra sino en lo que se llama el excéntrico. Las órbitas de los planetas en este sistema describen curvas epitrocoides.
El epiciclo gira y rota a lo largo del deferente con un movimiento uniforme. Sin embargo, Ptolomeo encontró que la razón a la que el deferente giraba no era constante a menos que fuera medida desde otro punto localizado a la misma distancia de la excéntrica, al que llamó ecuante. Lo que era constante era la razón angular a la que el deferente se movía alrededor del ecuante. Fue el uso de ese ecuante lo que distinguía al sistema ptolemaico.
Ptolomeo no predijo los tamaños relativos de los deferentes planetarios en el Almagesto. Todos sus cálculos se realizaron con respecto a un deferente normalizado. Esto no quiere decir que creyese que los planetas eran todos equidistantes. Hizo una conjetura y un ordenamiento de los planetas. Más tarde, calculó sus distancias en Hipótesis de los planetas.
Para los planetas exteriores, el planeta típicamente se mueve a través del cielo nocturno más lentamente que las estrellas. Cada noche, el planeta aparecería "desfasado" un poco por detrás de las estrellas próximas, en lo que se llama movimiento progrado. Ocasionalmente, cerca de la oposición, el planeta parece moverse a través del cielo nocturno más rápido que las estrellas, en el llamado movimiento retrógrado. El modelo ptolemaico, en parte, buscó explicar este comportamiento.
Los planetas interiores se observan siempre cerca del Sol, apareciendo poco antes del amanecer o poco después de la puesta del sol. Para solucionar esto, el modelo de Ptolomeo fijó el movimiento de Mercurio y de Venus para que la línea desde los puntos ecuantes al centro del epiciclo fuera siempre paralela a la línea Tierra-Sol.
Historia
[editar]
Cuando los antiguos astrónomos miraban el cielo, veían el Sol, la Luna y las estrellas moviéndose sobre ellos de una manera regular. También veían "vagabundos" o "planetai" (nuestros planetas). La regularidad en los movimientos de los cuerpos errantes sugería que sus posiciones podrían ser predecibles.
La aproximación más obvia para abordar el problema de la predicción de los movimientos de los cuerpos celestes fue simplemente delinear sus posiciones contra el campo de estrellas y luego encajar funciones matemáticas a las cambiantes posiciones.[1]
Los antiguos trabajaban desde una perspectiva geocéntrica por el mero hecho de que percibían que la Tierra estaba quieta y que es el cielo el que parece moverse. Sin embargo, Aristarco de Samos especuló que los planetas orbitaban el Sol. Empero, le faltaban herramientas matemáticas y ópticas, que llegaron mucho después, en la Modernidad.
Por otra parte, la física aristotélica afirmaba con énfasis la tesis de que el mundo supralunar era perfecto y que, por ello, los cuerpos celestes solo podían desplazarse con movimientos circulares y uniformes. El heliocentrismo cuestionaba dicha tesis.
Cuando Galileo Galilei observó las lunas de Júpiter el 7 de enero de 1610 y las fases de Venus en septiembre de 1610, el modelo heliocéntrico comenzó a recibir un amplio respaldo entre los astrónomos.
A continuación, Johannes Kepler, tomando las observaciones de Tycho Brahe, pudo formular sus famosas tres leyes del movimiento planetario y describió las órbitas de los planetas del sistema solar con una precisión increíble nunca antes vista. Las tres leyes de Kepler todavía se enseñan hoy en día en las clases de física universitaria y de astronomía.
El movimiento aparente de los astros con respecto al tiempo es cíclico en la naturaleza. Apolonio de Perga se dio cuenta de que esta variación cíclica podría representarse visualmente por pequeñas órbitas circulares o epiciclos, que giraban en órbitas circulares más grandes, o deferentes. Hiparco de Nicea calculó las órbitas necesarias y añadió que el centro de los deferentes no coincidía con la Tierra, considerada el centro del universo, sino que eran excéntricos.
Claudio Ptolomeo refinó el concepto deferente-epiciclo y presentó el ecuante como un mecanismo para la contabilización de las variaciones de velocidad en los movimientos de los planetas. La metodología empírica desarrollada demostró ser extraordinariamente precisa para sus días y aún estaba en uso en la época de Copérnico y Kepler.
Owen Gingerich[2] describió una conjunción planetaria ocurrida en 1504 que aparentemente observó Copérnico. En unas notas atadas con su copia de las Tablas alfonsíes, Copérnico comentó que «Marte supera los números en más de dos grados. Saturno es superado por los números en un grado y medio». Usando modernos programas informáticos, Gingerich descubrió que, en el momento de la conjunción, Saturno, en efecto, iba rezagado según las tablas en un grado y medio y Marte fallaba en las predicciones en casi dos grados. Sin embargo, encontró que las predicciones de Ptolomeo para Júpiter eran al mismo tiempo bastante precisas. Por lo tanto, Copérnico y sus contemporáneos estaban utilizando los métodos de Ptolomeo y los encontraban fiables casi más de mil años después de la que la obra original de Ptolomeo se publicase.
Cuando Copérnico transformó las observaciones realizadas desde la Tierra a coordenadas heliocéntricas,[3] se encontró con un problema totalmente nuevo. Las posiciones centradas en el Sol mostraban un movimiento cíclico con respecto al tiempo pero sin bucles retrógrados en el caso de los planetas exteriores. En principio, el movimiento heliocéntrico era el objetivo más fácil con nuevos matices, debido a la forma elíptica de las órbitas, todavía pendiente de descubrirse. Otro problema, que Copérnico nunca resolvió, consistió en representar correctamente el movimiento de la Tierra en la transformación de coordenadas.[4] Conservando las prácticas anteriores, utilizó la teoría de los modelos deferente y epiciclo en su teoría, pero sus epiciclos eran pequeños y se llamaron "epicicletos".
En el sistema ptoloméico, los modelos para cada uno de los planetas eran diferentes y así eran los modelos iniciales de Copérnico. Mientras trabajaba con las matemáticas, sin embargo, descubrió que sus modelos podían combinarse en un sistema unificado. Por otra parte, si se trataba la órbita de la Tierra a la misma escala que las demás, el orden de los planetas que hoy se reconoce fácilmente se podía obtener como consecuencia de razonamientos matemáticos. Mercurio orbitaba más cercano al Sol y la posición del resto de los planetas se desplazó hacia el espacio exterior, dispuestas sus órbitas en distancias proporcionales a sus períodos de revolución.[5]
Aunque los modelos de Copérnico reducían considerablemente la magnitud de los epiciclos, es discutible si eran más simples que los de Ptolomeo. Copérnico logró eliminar la denostada ecuante de Ptolomeo, pero a costa de agregar epiciclos adicionales. Varios libros del siglo XVI basados en Ptolomeo y Copérnico utilizan aproximadamente el mismo número de epiciclos.[6][7][8]
La idea de que Copérnico utilizó solo 34 círculos en su sistema proviene de sus propias palabras en un boceto preliminar inédito llamado Commentariolus. Empero, cuando publicó De revolutionibus orbium coelestium, ya había añadido más círculos. Finalmente, su sistema resultó tan complejo que resulta difícil contar el número total de epiciclos. A fin de cuentas, su sistema no resultó ser más simple que el de Ptolomeo.[9] Koestler, en su Historia de la Visión Humana del Universo, estima el número de epiciclos utilizados por Copérnico en 48.[10] La referencia popular de unos 80 círculos para el sistema ptolomeico parece haber surgido en 1898. Puede haber estado inspirada por el sistema no-ptolemaico de Girolamo Fracastoro, que usó 77 o 79 órbitas en su sistema inspirado en Eudoxo de Cnido.[11] Copérnico en sus obras exageró el número de epiciclos utilizados en el sistema ptolemaico, aunque los recuentos originales estaban alrededor de los 80 círculos.[12] Aunque los conteos iniciales aproximaban unos 80 círculos, en la época de Copérnico Peurbach había actualizado el sistema ptolemaico hasta llegar a unos 40, de ahí que Copérnico pudo reemplazar el problema de las retrogradaciones con más epiciclos.
Copérnico eliminó la ecuante de Ptolomeo, pero a costa de agregar epiciclos adicionales. Contar el número final es difícil, pero las estimaciones señalan que el sistema de Copérnico era tanto o más complicado que el de Ptolomeo.
La teoría de Copérnico era tan precisa, al menos, como la de Ptolomeo, pero nunca alcanzó la estatura y el reconocimiento de ésta. Los trabajos de Copérnico proporcionaban explicaciones a fenómenos como el movimiento retrógrado, pero realmente no probaban que los planetas giraran alrededor del Sol. Lo que hacía falta era la teoría elíptica de Kepler, que no llegó hasta 1609.

Las teorías de Ptolomeo y Copérnico probaron la durabilidad y la capacidad de adaptación del dispositivo deferente-epiciclo para representar el movimiento planetario. Este modelo funcionaba tan bien como lo hizo debido a la extraordinaria estabilidad orbital del sistema solar. De hecho, se podría utilizar aún hoy con éxito.[13]
El primer modelo planetario sin ningún epiciclo fue el de Ibn Bajjah (Avempace) en el siglo XII en la España andalusí,[14] pero los epiciclos no se eliminaron en Europa hasta el siglo XVII, cuando el modelo de las órbitas elípticas de Johannes Kepler remplazó gradualmente al de Copérnico basándose en círculos perfectos.
La mecánica clásica o newtoniana eliminó la necesidad de métodos deferente-epiciclo y produjo teorías mucho más poderosas. Tratando el Sol y los planetas como masas puntuales y usando la ley de la gravitación universal, se derivaban las ecuaciones del movimiento que podían resolverse por diversos medios para calcular las predicciones de las velocidades y las posiciones orbitales planetarias. El simple problema de los dos cuerpos, por ejemplo, podía resolverse analíticamente. El más complejo problema de los n cuerpos requiere métodos numéricos para su solución.
El poder de la mecánica newtoniana para resolver problemas de mecánica orbital se ilustra por el descubrimiento de Neptuno. El análisis de las perturbaciones observadas en la órbita de Urano llevó a realizar unas estimaciones sobre la posición de un supuesto planeta en una zona del firmamento donde fue encontrado. Este descubrimiento no podría haberse logrado con los métodos deferente-epiciclo. Aun así, en 1702 Newton publicó Theory of the Moon's Motion, en el que empleaba un epiciclo y permaneció en uso en China en el siglo XIX. Las tablas subsecuentes basadas en la Teoría de Newton podrían tener una exactitud del orden del arco de minuto.[15]
Epiciclos
[editar]Según una escuela de pensamiento en la historia de la astronomía, se descubrieron mediante observaciones algunas imperfecciones menores en el sistema original de Ptolomeo que fueron acumulándose en el tiempo. Se creía erróneamente que se añadieron más niveles de epiciclos (círculos dentro de círculos) a los modelos para que coincidiesen con mayor precisión con los movimientos planetarios observados. La multiplicación de los epiciclos se creía que habría dado lugar a un sistema casi impracticable en el siglo XVI y que Copérnico habría concebido su sistema heliocéntrico con el fin de simplificar la astronomía ptolemaica de su época, logrando así reducir drásticamente el número de círculos.
Con mejores observaciones, se utilizaron epiciclos adicionales y excéntricos para representar los fenómenos recién observados hasta fines de la Edad Media, el universo se hizo una 'Esfera /con garabateado céntrico y excéntrico /Ciclo y Epiciclo, Orbe sobre Orbe'.With better observations additional epicycles and eccentrics were used to represent the newly observed phenomena till in the later Middle Ages the universe became a 'Sphere/With Centric and Eccentric scribbled o'er,/Cycle and Epicycle, Orb in Orb' –Dorothy Stimson[16]
Como medida de tal complejidad, el número de círculos dado por Ptolomeo era de 80, en comparación con los solo 34 de Copérnico.[17] El número más alto aparece en la Encyclopaedia Britannica sobre astronomía durante la década de 1960, en un debate sobre el interés del rey Alfonso X de Castilla en la astronomía en el siglo XIII (a Alfonso se le atribuye el encargo de las Tablas alfonsinas.)
En ese momento cada planeta debía tener de 40 a 60 epiciclos para representar de manera efectiva su complejo movimiento entre las estrellas. Asombrado por la dificultad del proyecto, se dice que Alfonso comentó que "de haber estado presente en el momento de la creación, podría haber dado excelentes consejos al respecto".By this time each planet had been provided with from 40 to 60 epicycles to represent after a fashion its complex movement among the stars. Amazed at the difficulty of the project, Alfonso is credited with the remark that had he been present at the Creation he might have given excellent advice.Encyclopaedia Britannica[18]
Como resultado, una de las principales dificultades de esta teoría de epiciclos en epiciclos es que los historiadores que han examinado los libros sobre astronomía ptolemaica de la Edad Media y del Renacimiento, no han encontrado absolutamente ningún rastro de que se hayan utilizado múltiples epiciclos para cada planeta. Las Tablas alfonsinas, por ejemplo, se calcularon aparentemente utilizando los métodos originales de Ptolomeo sin adornos.[19]
Otro problema es que los modelos mismos desalentaban los retoques. En un modelo deferente-epiciclo, las partes y el todo están interrelacionadas. Un cambio en un parámetro para mejorar el ajuste en un lugar desajusta mucho en otro lugar. El modelo de Ptolomeo es probablemente óptimo en este sentido. En conjunto, dio buenos resultados pero falló un poco aquí y allá. Los astrónomos experimentados habrían conocido estas deficiencias y habían recurrido a atajos para resolverlos.
Argot de mala ciencia
[editar]En parte debido a los malentendidos acerca de cómo trabajaban los modelos deferente-epiciclo, la expresión "añadiendo epiciclos" ha llegado a utilizarse como término despectivo en la discusión científica moderna. Puede usarse, por ejemplo, para describir el continuo ajuste de una teoría para hacer predicciones que coincidan con los hechos. De acuerdo con esta noción, algunos han considerado los epiciclos como el ejemplo paradigmático de mala ciencia.[20] Parte del problema puede ser debido a la idea errónea del epiciclo como explicación del movimiento de un cuerpo en lugar de simplemente como una descripción. Toomer lo explica de la siguiente manera:
Mientras que usamos "hipótesis" para denotar una teoría tentativa que aún no se ha verificado, Ptolomeo usualmente entiende por ύπόθεσις algo más parecido a un "modelo", o "sistema de explicación", a menudo refiriéndose a "las hipótesis que hemos demostrado".Whereas we use 'hypothesis' to denote a tentative theory which is still to be verified, Ptolemy usually means by ύπόθεσις something more like 'model', 'system of explanation', often indeed referring to 'the hypotheses which we have demonstrated'."[21]
Formalismo matemático
[editar]Según el historiador de la ciencia Norwood Russell Hanson:
No existe una curva bilateral simétrica ni exógenamente periódica utilizada en ninguna rama de la astrofísica o de la astronomía observacional que no pueda trazarse fácilmente como el movimiento resultante de un punto que gira dentro de una constelación de epiciclos, finitos en número, que giran alrededor de un punto fijo deferente.There is no bilaterally-symmetrical, nor excentrically-periodic curve used in any branch of astrophysics or observational astronomy which could not be smoothly plotted as the resultant motion of a point turning within a constellation of epicycles, finite in number, revolving around a fixed deferent.Norwood Russell Hanson[22]
Cualquier trayectoria (periódica o no, cerrada o abierta) puede representarse con un número infinito de epiciclos. Esto se debe a que los epiciclos pueden representarse como series de Fourier complejas; así que, con un amplio número de epiciclos, las trayectorias muy complicadas pueden representarse en el plano complejo.[23]
Sea el número complejo:
donde:
- y son constantes,
- es el número imaginario y
- es el tiempo, que corresponde a un deferente centrado en el origen del plano complejo y girando con un radio y velocidad angular
dónde es el periodo.
Si es la trayectoria de un epiciclo, entonces el deferente más el epiciclo se representa como la suma:
.
Generalizando a epiciclos:
,
que es un tipo particular de complejo de la serie de Fourier conocido como función casi periódica de Besicovitch. Encontrando los coeficientes para representar una trayectoria dependiente del tiempo en el plano complejo, , es posible alcanzar el objetivo de reproducir una órbita con deferente y epiciclos, y esta es una manera de "justificación de fenómenos" (σώζειν τα φαινόμενα).[24]
este paralelismo fue obsorvó ebservado.[25] Respecto al debate de la revolución de Copérnico frente al debate del formalismo de las explicaciones científicas, puede entenderse por qué Tomás de Aquino, en el siglo XIII, escribió:
La razón puede emplearse de dos maneras para establecer un punto: en primer lugar, con el fin de proporcionar pruebas suficientes de algún principio [...]. La razón también se emplea de otra manera, no como una prueba suficiente de un principio, sino como una confirmación de un principio ya establecido, mostrando la congruencia de sus resultados, ya que en astronomía se considera establecida la teoría de los círculos excéntricos y epiciclos, porque de ese modo se pueden explicar las apariencias sensibles de los movimientos celestiales; no, sin embargo, como si esta prueba fuera suficiente, ya que alguna otra teoría podría explicarlos. [...]Reason may be employed in two ways to establish a point: firstly, for the purpose of furnishing sufficient proof of some principle [...]. Reason is employed in another way, not as furnishing a sufficient proof of a principle, but as confirming an already established principle, by showing the congruity of its results, as in astronomy the theory of eccentrics and epicycles is considered as established, because thereby the sensible appearances of the heavenly movements can be explained; not, however, as if this proof were sufficient, forasmuch as some other theory might explain them. [...][26]
Véase también
[editar]Notas
[editar]- ↑ Para un ejemplo de la complejidad del problema, ver Owen Gingerich, The Book Nobody Read, Walker, 2004, p. 50.
- ↑ Gingerich, Chapter 4
- ↑ Un volumen de de Revolutionibus fue dedicado a una descripción de la trigonometría usada para hacer la transformación entre las coordenadas geocéntricas y heliocéntricas.
- ↑ Gingerich, p. 267.
- ↑ Gingerich, p. 54.
- ↑ Robert Palter, Approach to the History of Astronomy, en Studies in the History and Philosophy of Science 1 (1970): 94.
- ↑ Owen Gingerich, Alfonso X as a Patron of Astronomy, en The Eye of Heaven: Ptolemy, Copernicus, Kepler (New York: American Institute of Physics, 1993), p. 125.
- ↑ Gingerich, Crisis versus Aesthetic in the Copernican Revolution, en Eye of Heaven, pp. 193–204.
- ↑ «La creencia popular de que el sistema heliocéntrico copernicano constituye una significativa simplificación del sistema ptolomeico es obviamente errónea. Los mismos modelos copernicanos requieren aproximadamente el doble de círculos que los modelos de Ptolomeo y son mucho menos elegantes y adaptables». ("The popular belief that Copernicus's heliocentric system constitutes a significant simplification of the Ptolemaic system is obviously wrong ....[T]he Copernican models themselves require about twice as many circles as the Ptolemaic models and are far less elegant and adaptable.), Neugebauer, Otto (1969) [1957]. The Exact Sciences in Antiquity (2 edición). Dover Publications. ISBN 978-0-486-22332-2., p. 204. Esta es una estimación extrema a favor de Ptolomeo.
- ↑ Koestler, Arthur (1989) [1959]. The Sleepwalkers. Arkana, Penguin Books., p. 195
- ↑ Palter, Approach to the History of Astronomy, pp. 113–14.
- ↑ Koestler, Arthur (1989) [1959]. The Sleepwalkers. Arkana, Penguin Books., p. 194-195.
- ↑ Un modelo deferente/epiciclo es de hecho utilizado para calcular las posiciones lunares necesarias para la definición de los modernos calendarios hindúes. Véase Nachum Dershovitz y Edward M. Reingold: Calendrical Calculations, Cambridge University Press, 1997, capítulo 14. (ISBN 0-521-56474-3)
- ↑ Bernard R. Goldstein (March 1972). Theory and Observation in Medieval Astronomy, Isis 63 (1), p. 39–47 [40–41].
- ↑ Kollerstrom, Nicholas (2000). Newton's Forgotten Lunar Theory. Green Lion Press. ISBN 1-888009-08-X.
- ↑ Dorothy Stimson, The Gradual Acceptance of the Copernican Theory of the Universe (New York, 1917), p. 14. La cita es de El paraíso perdido de John Milton, Libro 8, 11.82–85.
- ↑ Robert Palter, An Approach to the History of Early Astronomy
- ↑ Encyclopaedia Britannica, 1968, vol. 2, p. 645. Este número se cita como el más alto en la obra de Owen Gingerich Alfonso X. Gingerich también expresó sus dudas acerca de la cita atribuida a Alfonso. En The Book Nobody Read (El libro que nadie lee) (p. 56), sin embargo, Gingerich señala que había desafiado a la Encyclopaedia Britannica acerca del número de epiciclos. La respuesta que obtuvo es que el autor original de la entrada había muerto y que su fuente no podía ser verificada.
- ↑ Gingerich, The Book Nobody Read (p. 57).
- ↑ Ver por ejemplo, Kolb, Rocky, Blind Watchers of the Sky, Addison–Wesley, 1996. P. 299 (ISBN 0-201-48992-9)
- ↑ Toomer, G.J. (1998). Ptolemy's Almagest. Princeton University Press. p. 23. ISBN 0-691-00260-6.
- ↑ Hanson, Norwood Russell (1 de junio de 1960). «The Mathematical Power of Epicyclical Astronomy». Isis 51 (2): 150-158. ISSN 0021-1753. JSTOR 226846. doi:10.1086/348869. Archivado desde el original el 1 de noviembre de 2020. Consultado el 21 de octubre de 2011.
- ↑ Véase, por ejemplo, this animation animación realizada por Christián Carman y Ramiro Serra, que usa 10.000 epiciclos para reproducir la silueta de Homer Simpson; cf. y también a Christián Carman en Deferentes, epiciclos y adaptaciones, y “La refutabilidad del Sistema de Epiciclos y Deferentes de Ptolomeo.”
- ↑ Cf. Duhem, Pierre (1969). To save the phenomena, an essay on the idea of physical theory from Plato to Galileo. Chicago: University of Chicago Press. OCLC 681213472. (excerpt).
- ↑ Giovanni Gallavotti: Quasi periodic motions from Hipparchus to Kolmogorov. In: Rendiconti Lincei – Matematica e Applicazioni. Series 9, Band 12, No. 2, 2001, p. 125–152 (PDF; 205 KB)
- ↑ Summa Theologica, I q. 32 a. 1 ad 2
Referencias
[editar]Enlaces externos
[editar] Wikimedia Commons alberga una categoría multimedia sobre Epiciclo.
Wikimedia Commons alberga una categoría multimedia sobre Epiciclo.- El derrumbe del universo ptolomeico, en historiadelaciencia
- Ptolemaic System - en el Proyecto Galileo de la Universidad de Rice.
- Eccentrics, Deferents, Epicycles, and Equants - en MathPages
Ilustraciones animadas
[editar]- Java simulation of the Ptolemaic System – en el Planetario Virtual Animado de Paul Stoddard, de la Northern Illinois University
- Epicycle and Deferent Demo – en el sitio web de Rosemary Kennett de la Universidad de Syracuse
- Una animación flash que muestra epiciclos con parámetros ajustables y presets para varios planetas.
- un applet que muestra el principio de la epiciclo, con una comparación de los modelos geocéntrico y heliocéntrico.


 French
French Deutsch
Deutsch











