Magnetyczny moment dipolowy – Wikipedia, wolna encyklopedia

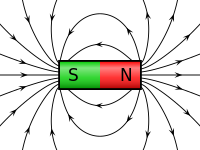
Magnetyczny moment dipolowy ${\displaystyle {\vec {\mu }}}$ (lub ${\displaystyle p_{\mathrm {m} }}$) – pseudowektorowa wielkość fizyczna cechująca dipol magnetyczny, która określa pole magnetyczne wytwarzane przez ciało oraz oddziaływanie dipola z zewnętrznym polem magnetycznym.

Magnetyczny moment dipolowy ${\displaystyle \mu }$ definiuje się przez moment siły ${\displaystyle M}$ działający na niego w jednorodnym polu magnetycznym o indukcji ${\displaystyle B}$^[1]:

${\displaystyle {\vec {M}}={\vec {\mu }}\times {\vec {B}}.}$

Oddziaływanie magnetyczne ciała z jednorodnym polem magnetycznym niezgodne z oddziaływaniem dipola o wartości niezależnej od położenia przedstawia się w postaci szeregu multipolowego, którego pierwszym składnikiem jest moment dipolowy. Zazwyczaj składnikiem dominującym jest oddziaływanie wynikające z magnetycznego momentu dipolowego, a pozostałe wyrazy szeregu multipolowego są małe i mogą być pomijane. Dlatego powszechne jest nazywanie dipolowego momentu magnetycznego po prostu momentem magnetycznym. Czasami jednak obserwuje się także efekty istnienia niedipolowych składowych momentu magnetycznego^[2].

Jednostką momentu magnetycznego w układzie SI jest amper razy metr kwadrat [${\displaystyle A\cdot m^{2}}$ = ${\displaystyle {\frac {J}{T}}}$].

W fizyce atomowej mierzy się go w magnetonach Bohra (tu magnetyzm wynika z obecności elektronów w atomie)^[3]:

1 ${\displaystyle \mu _{B}\approx 10^{-23}}$ [${\displaystyle {\frac {J}{T}}}$].

W fizyce jądrowej wyraża się go w magnetonach jądrowych, przy opisie znacznie słabszego magnetyzmu jąder i nukleonów^[4]:

1 ${\displaystyle \mu _{N}\approx 5\cdot 10^{-27}}$ [${\displaystyle {\frac {J}{T}}}$].

Gdy przez prostokątną ramkę umieszczoną w jednorodnym polu magnetycznym płynie prąd, to działa na nią moment siły proporcjonalny do pola ramki oraz natężenia prądu w ramce, co oznacza, że ramka z prądem jest dipolem magnetycznym. Identyczne oddziaływanie zachodzi dla każdej ramki z prądem w jednorodnym polu magnetycznym^[1].

Gdy w przewodzie płynie prąd elektryczny, to wytwarza on pole magnetyczne. Jeżeli przewód jest cienki i tworzy zamkniętą płaską pętlę, to oddziałuje z jednorodnym polem magnetycznym tak jak dipol o momencie magnetycznym określonym wzorem^[1][5]:

${\displaystyle {\vec {\mu }}=I{\vec {S}},}$

gdzie:

${\displaystyle {\vec {\mu }}}$ – dipolowy moment magnetyczny [${\displaystyle A\cdot m^{2}}$] lub [${\displaystyle {\frac {J}{T}}}$],

${\displaystyle {\vec {S}}}$ – wektor powierzchniowy o wartości równej polu powierzchni zamkniętej przez pętlę z prądem [${\displaystyle m^{2}}$],

${\displaystyle I}$ – stałe natężenie prądu [${\displaystyle A}$].

Moment dipolowy jest wektorem (dokładniej pseudowektorem) skierowanym prostopadle do powierzchni pętli, o zwrocie określonym regułą prawej dłoni. Jeżeli palce prawej dłoni wskazują kierunek przepływu prądu w pętli, to odwiedziony kciuk wskazuje zwrot momentu magnetycznego^[1].

Dla ośrodków ciągłych, w których płyną prądy elektryczne, moment magnetyczny definiuje się jako całkę objętościową z iloczynu wektorowego wektora wodzącego ${\displaystyle {\vec {r}}}$ i gęstości prądu ${\displaystyle {\vec {j}}}$ zadanego w punkcie ${\displaystyle {\vec {r}}{:}}$

${\displaystyle {\vec {\mu }}={\frac {1}{2}}\int _{V}{\vec {r}}\times {\vec {j}}({\vec {r}})\,dV.}$

• Moment magnetyczny układu dyskretnych, poruszających się ładunków:

${\displaystyle {\vec {\mu }}={\frac {1}{2}}\sum \limits _{k=1}^{n}q_{k}{\vec {r}}_{k}\times {\vec {v}}_{k},}$

gdzie ${\displaystyle q_{k}}$ oznacza ${\displaystyle k}$-ty ładunek, zaś ${\displaystyle {\vec {r}}_{k}}$ i ${\displaystyle {\vec {v}}_{k}}$ oznaczają odpowiednio jego wektor wodzący i wektor prędkości.

Moment magnetyczny magnesu sztabkowego wyraża wzór:

${\displaystyle {\vec {\mu }}=m\cdot {\vec {l}},}$

gdzie ${\displaystyle m}$ jest wartością mas magnetycznych skupionych na końcach magnesu, a ${\displaystyle {\vec {l}}}$ jest wektorem łączącym masę magnetyczną bieguna południowego z północną.

Sens fizyczny wyboru zwrotu momentu magnetycznego według wyżej podanej definicji jest następujący: jeżeli dipol oddziałując z zewnętrznym polem magnetycznym ustawi się tak, że przyjmie minimum energii potencjalnej, to jego biegun ${\displaystyle N}$ znajdzie się bliżej bieguna ${\displaystyle S}$ ciała, wytwarzającego to pole; wtedy wektor magnetyczny ${\displaystyle {\vec {\mu }}}$ dipola będzie skierowany zgodnie ze zwrotem wektora indukcji magnetycznej ${\displaystyle {\vec {B}}}$ pola.

Zgodnie z definicją dipola magnetycznego, na ciało posiadające magnetyczny moment dipolowy umieszczone w zewnętrznym polu magnetycznym działa moment siły^[6]:

${\displaystyle {\vec {M}}={\vec {\mu }}\times {\vec {B}},}$

gdzie:

${\displaystyle {\vec {M}}}$ – moment siły [${\displaystyle N\cdot m}$],

${\displaystyle {\vec {\mu }}}$ – moment magnetyczny [${\displaystyle A\cdot m^{2}}$],

${\displaystyle {\vec {B}}_{zewn}}$ – indukcja pola magnetycznego [${\displaystyle T}$].

Moment siły działający na dipol magnetyczny z polem magnetycznym ma energię potencjalną zależną od ustawienia dipola względem pola^[7]:

${\displaystyle U=-{\vec {\mu }}\cdot {\vec {B}},}$

${\displaystyle U=-\mu \cdot B\cos \theta .}$

Energia ta zależy od kąta między wektorem momentu magnetycznego a wektorem indukcji magnetycznej. Gdy wektory te mają przeciwne zwroty, to energia potencjalna jest maksymalna, zaś dla zwrotów zgodnych – minimalna.

W wyniku oddziaływania dipola z polem dipol może zacząć obracać się, dążąc do uzyskania minimum energii potencjalnej. Tracona energia zamienia się na energię kinetyczną jego ruchu obrotowego lub energię promieniowania. W przypadku cząstek mikroskopowych mogę one tracić lub zyskiwać energię potencjalną w polu w sposób skwantowany (skokowy).

Na dipol magnetyczny umieszczony w niejednorodnym polu magnetycznym działa siła proporcjonalna do gradientu indukcji magnetycznej^[8]:

${\displaystyle {\vec {F}}=\nabla \left({\vec {\mu }}\cdot {\vec {B}}\right).}$

Moment magnetyczny cząstki mikroskopowej powstaje na skutek jej ruchu w przestrzeni (np. ruch orbitalny elektronu w atomie) lub jest to tzw. wewnętrzny moment magnetyczny, nie związany z żadnym ruchem – mają go cząstki obdarzone spinem (przy czym moment magnetyczny jest związany ze spinem poprzez czynnik giromagnetyczny)^[9].

Niezerowy moment magnetyczny mogą mieć cząstki obdarzone ładunkiem elektrycznym, np. elektron, proton, jak też cząstki elektrycznie obojętne, np. neutron.

Zgodnie z modelem atomu podanym przez Bohra elektron krąży po orbicie kołowej, co oznacza przepływ elementarnego prądu elektrycznego. Prąd ten wytwarza pole magnetyczne, którego wartość oraz ukierunkowanie w przestrzeni można scharakteryzować za pomocą wektora momentu magnetycznego – wektor ten nosi nazwę orbitalnego momentu magnetycznego elektronu.

Moment pędu elektronu jest wielkością skwantowaną (przyjmuje wielokrotność zredukowanej stałej Plancka), a co za tym idzie, moment magnetyczny także jest skwantowany i zależny od tzw. magnetycznej liczby kwantowej. Dla orbitalnej liczby kwantowej ${\displaystyle n=1,}$ orbitalny moment magnetyczny ma najmniejszą wartość zwaną magnetonem Bohra.

Dokładniejszego opisu własności magnetycznych atomu dostarczają równanie Pauliego i równanie Diraca, które pokazują, że elektron w atomie posiada oprócz orbitalnego momentu magnetycznego także tzw. własny moment pędu (zwany spinem) oraz związany z nim spinowy moment magnetyczny. (Równania te uogólniają podstawowe równane mechaniki kwantowej – równanie Schrödingera – na przypadek cząstek za spinem, przy czym równanie Diraca spełnia dodatkowo warunek relatywistycznej niezmienniczości, i dlatego jest dokładniejsze niż równanie Pauliego.)

Moment magnetyczny elektronu w oddziaływaniu z zewnętrznym polem magnetycznym przyjmuje jeden z dyskretnych stanów, przy czym rzut orbitalnego momentu magnetycznego elektronu na kierunek pola magnetycznego określa wzór^[10]

${\displaystyle \mu _{z}=-\mu _{B}m,}$

gdzie:

${\displaystyle \mu _{B}={\frac {e\hbar }{2m_{e}}}}$ – magneton Bohra,

${\displaystyle m}$ oznacza magnetyczną orbitalną liczbę kwantową.

Rzut spinowego momentu magnetycznego na kierunek pola magnetycznego jest określony wzorem^[10]:

${\displaystyle \mu _{sz}=-g_{s}\mu _{B}m_{s}\approx \pm \mu _{B},}$

gdzie:

${\displaystyle m_{sz}=\pm {\frac {1}{2}}}$ oznacza magnetyczną spinową liczbę kwantową.

Wielkość ${\displaystyle g_{s}}$ nazywana jest stosunkiem żyromagnetycznym. Równanie Diraca przewiduje jego wartość równą ${\displaystyle 2.}$ Z pomiarów otrzymuje się wartość nieco większą. (Dokładną wartość tej stałej przewiduje elektrodynamika kwantowa, uwzględniająca dodatkowo zjawisko oddziaływania elektronu z cząstkami w próżni kwantowej).

Całkowity orbitalny moment magnetyczny elektronu zależy od liczby kwantowej ${\displaystyle l}$ momentu pędu elektronu^[10]

${\displaystyle \mu _{orbita}=-\mu _{B}{\sqrt {l(l+1)}},}$

a całkowity spinowy moment magnetyczny elektronu (zależny od liczby spinowej ${\displaystyle s={\frac {1}{2}}}$)^[10]

${\displaystyle \mu _{spin}=-g_{s}\mu _{B}{\sqrt {s(s+1)}}=-{\sqrt {3}}\mu _{B}.}$

Powyższe momenty magnetyczne są zdefiniowane jako liczby ujemne, co oznacza, że wektory magnetyczne są skierowane przeciwnie odpowiednio do wektorów momentu pędu elektronu orbitalnego i spinowego^[9]. Elektrony na skutek posiadania momentów magnetycznych wykazują zjawisko elektronowego rezonansu spinowego. Zjawisko to jest wykorzystywane w spektroskopii elektronowego rezonansu spinowego, zwanej również elektronowym rezonansem paramagnetycznym EPR.

Na moment magnetyczny atomu składają się: wypadkowy moment magnetyczny elektronów oraz moment magnetyczny jądra. W wektorowym modelu atomu wprowadza się całkowity moment pędu elektronu, który jest sumą orbitalnego i spinowego momentu pędu. Całkowity moment magnetyczny atomu wynosi^[10]:

${\displaystyle \mu _{atom}=g_{J}\mu _{B}{\sqrt {J(J+1)}},}$

gdzie:

${\displaystyle J=L+S,L+S-1,\dots ,|L-S|}$ – liczba kwantowa całkowitego momentu pędu atomu, zależna od liczby ${\displaystyle L}$ całkowitego orbitalnego momentu pędu atomu oraz od liczby ${\displaystyle S}$ całkowitego spinowego momentu pędu,

${\displaystyle g_{J}}$ – czynnik Landego,

w którym

${\displaystyle g_{J}=1+{\frac {J(J+1)+S(S+1)-L(L+1)}{2J(J+1)}}.}$

Moment magnetyczny jądra w atomie jest pomijalnie mały w stosunku do momentów magnetycznych elektronów (jest on około tysiąc razy mniejszy – patrz tabela niżej). Jednak dzięki specjalnym technikom badawczym (NMR, spektroskopia Mössbauerowska itp.) jest on mierzalny.

Analogicznie do całkowitego momentu magnetycznego elektronów, moment magnetyczny jądra ma składową spinową (pochodzącą od sumowania wkładów spinowych momentów magnetycznych nukleonów) oraz składową wynikającą z orbitalnego ruchu protonów na powłokach jądrowych.

Jądra atomów na skutek posiadania momentów magnetycznych wykazują zjawisko jądrowego rezonansu magnetycznego. Zjawisko to jest wykorzystywane w spektroskopii magnetycznego rezonansu jądrowego (spektroskopii NMR, z ang. nuclear magnetic resonance).

Momenty magnetyczne i spiny niektórych cząstek

Cząstka	Dipolowy moment magnetyczny [10−27 ${\displaystyle {\frac {J}{T}}}$]	Spin (${\displaystyle \hbar }$)
elektron	−9284,764	${\displaystyle {\frac {1}{2}}}$
proton	+14,106067	${\displaystyle {\frac {1}{2}}}$
neutron	−9,66236	${\displaystyle {\frac {1}{2}}}$
mion	−44,904478	${\displaystyle {\frac {1}{2}}}$
deuteron	+4,3307346	${\displaystyle 1}$
tryt	+15,046094	${\displaystyle {\frac {1}{2}}}$

• elektryczny moment dipolowy
• elektrodynamika klasyczna
• kwadrupol
• moment elektromagnetyczny maszyn elektrycznych
• spin

• Jerzy Bodzenta: Wykłady z fizyki. Gliwice: Wydawnictwo Pracowni Komputerowej Jacka Skalmierskiego, 2004. ISBN 83-89105-66-7.
• Jerzy Kuryłowicz: Słownik fizyczny. Warszawa: Wydawnictwo „Wiedza Powszechna”, 1984. ISBN 83-214-0053-1. Brak numerów stron w książce