Perspectiva – Wikipédia, a enciclopédia livre

 Nota: Para outros significados, veja Perspectiva (desambiguação).

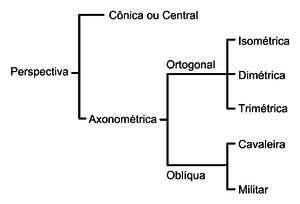
Perspectiva ^{(português brasileiro)} ou perspetiva ^{(português europeu)} é um campo de estudo da geometria e, em especial, da geometria projetiva. Suas aplicações estendem-se para: arte, arquitetura, design, engenharia etc. Trata-se de uma ciência que abarca os métodos de representação dos objetos em seus tamanhos e posições "corretas", tal qual a visão humana supostamente os compreenderia, a partir de um observador. A perspectiva subdivide-se em várias modalidades como: cônica, isométrica, cavaleira, militar, entre outras, e foi desenvolvida pelos artistas e geômetras na transição da Idade Média para o Renascimento, na sua forma estrita de entendimento.^[1]

Segundo Thomas E. French, ex-profesor de desenho de engenharia na Universidade Estadual de Ohio, e Charles J. Vierck, ex-professor de expressão gráfica da Universidade da Flórida, existia, na prática, até o final da década de 1990, três tipos de desenho em perspectiva, sendo eles: axonométrico (isométrico, dimétrico e trimétrico), oblíquo (em múltiplas variações) e os exatos (também classificados como centrais, que são compostos por um ou mais pontos de fuga).^[2]

Ver artigo principal: Perspectiva (gráfica)

A perspectiva com um ponto de fuga, também conhecida como perspectiva renascentista, foi o primeiro método de perspectiva exata, que se baseia em um ponto de fuga situado na linha do horizonte, para o qual convergem as retas paralelas, que ao serem transformadas em diagonais, no quadro, provocam a sensação de profundidade.^[3]

Ver artigo principal: Perspectiva com um ponto de fuga

A perspectiva com dois pontos de fuga é um método de perspectiva exata desenvolvido por Brook Taylor, em 1715, que abarca os processos: das dominantes, das fugantes, dos arquitetos, entre outros.^[4] Em 1719, Taylor lançou uma versão melhorada do trabalho em New Principles of Linear Perspective.^[5]

Ver artigo principal: Perspectiva com dois pontos de fuga

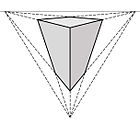
A perspectiva com três pontos de fuga é um processo de projeção central, em que um ponto de fuga está situado fora da altura dos olhos (linha do horizonte). É muito usado para ilustrar, com "exagero",^[6] uma cena observada de baixo para cima ou de cima para baixo, embora possa abrigar outras relações entre os elementos do sistema projetivo.^[7]

Ver artigo principal: Perspectiva com três pontos de fuga

O processo gráfico de perspectiva curvilínea foi usado para desenhar objetos em uma superfície plana, com a intenção de criar a sensação de que se está a observar uma superfície curvílina. Artistas como Jan van Eyck e Escher desenvolveram trabalhos com esse tipo de representação. Em 1968 um processo esférico foi codificado pelos artistas e historiadores André Barre e Albert Flocon, no livro La Perspective curviligne^[8], que foi traduzido para o inglês, em 1987, como Curvilinear Perspective: From Visual Space to the Constructed Image.^[9]

Ver artigo principal: Perspectiva curvilínea

A perspectiva quadridimensional é um processo contemporâneo, desenvolvido em 1997, que cria cenas com diferentes pontos de vista, os quais foram "vistos" por um observador móvel (o desenhista) e que podem ser registrados em superfícies planas ou curvilíneas.^[10]

Ver artigo principal: Perspectiva quadridimensional

Resultam da projeção cilíndrica ortogonal, quando três faces de um objeto podem ser vistas. Existem infinitas modalidades de perspectivas axonométricas, mas somente algumas são usadas com regularidade no desenho técnico.

A perspectiva isométrica é um caso particular de projeção cilíndrica ortogonal. O sistema de eixos da situação a ser projetada ocorrerá na perspectiva, se vistos no plano, de forma equi-angular a 120º. Desta forma, é possível traçar uma perspectiva isométrica através de uma malha de retas desenhadas a partir de ângulos de 30º.^[11][12] O termo isométrica vem do grego: "mesma medida", já que as medidas ortogonais, retiradas das vistas ortogonais, são redesenhadas nos eixos x, y e z com os tamanhos indicados pelas cotas. As linhas inclinadas, que estão fora do tri-eixo ortogonal, não têm as mesmas medidas.^[13]

Ver artigo principal: Perspectiva isométrica

O que caracteriza a perspectiva dimétrica é o fato de que dois de seus eixos projetam-se em ângulos iguais no quadro. A escala gráfica de construção é semelhante à da projeção isométrica, mas para ser desenhada são aplicados coeficientes de redução nos eixos horizontais.^[12][14]

Ver artigo principal: Perspectiva dimétrica

Na perspectiva trimétrica três ângulos do triedro de referência projetam-se em ângulos desiguais no quadro, desse modo os três eixos devem ser submetidos a coeficientes de redução diferentes.^[12][14]

Ver artigo principal: Perspectiva trimétrica

A perspectiva cavaleira é um tipo de projeção cilíndrica obliqua, estando o objeto com uma face paralela ao quadro (plano de projeção). Ela é considerada um método de perspectiva rápida, em virtude da facilidade com que se pode obter o desenho de objetos de dimensões reduzidas, principalmente se este tiver superfícies planas. Geralmente, o quadro é posicionado na vertical, mas se for colocado na horizontal, constituirá a projeção cilíndrica obliqua uma variedade da perspectiva cavaleira, a qual os autores franceses,^[15] no começo do século XIX, denominaram de perspectiva militar.^[12]

Ver artigo principal: Perspectiva cavaleira

Ver artigo principal: Perspectiva militar

• Escorço. Técnica de representação gráfica, na qual um objeto ou uma distância parecem mais curtos do que são na realidade. O termo deriva do verbo italiano scorciare que significa encurtar.^[16]
• Perspectiva atmosférica. Técnica de pintura na qual a atmosfera altera as tonalidades dos objetos mais distantes, diminuindo a saturação dos matizes. É o mesmo que perspectiva aérea ou perspectiva tonal.
• Perspectiva axial. A perspectiva axial, também conhecida como perspectiva angular, é um sistema em que linhas paralelas convergem para diferentes pontos de um eixo.^[17]
• Perspectiva espinha de peixe. Método de representação medieval, pré perspectivista, cujas retas inclinadas, as diagonais que geram a sensação de profundidade no quadro, convergem para um eixo central, ao contrário do ocorrerá nos métodos renascentistas, onde as retas convergirão para o ponto de fuga.^[18]
• Perspectiva Pictorum et Architectorum. O tratado Perspectiva Pictorum et Architectorum foi escrito, por Andrea Pozzo, com o intuito de oferecer aos pintores e arquitetos, o estado da arte da perspectiva. Os dois volumes que compõem a obra foram publicados em 1693 e 1700, respectivamente.
• Perspectiva hierárquica. A perspectiva hierárquica, usada desde a antiguidade, alterava o dimensionamento das figuras de acordo com a hierarquia dos personagens. Ela foi, por vezes, chamada de 'simbólica', embora toda representação em perspectiva passe por um processo de simbolização. É um tipo de representação, na qual os personagens têm uma dimensão que varia de acordo com a sua importância ou dignidade.^[1]

Referências

• Portal da arte

Este artigo sobre arte ou história da arte é um esboço. Você pode ajudar a Wikipédia expandindo-o. v d e

Este artigo sobre geometria é um esboço. Você pode ajudar a Wikipédia expandindo-o. v d e