Локальный уровень выброса — Википедия

Локальный уровень выброса — алгоритм^{[уточнить]} нахождения аномальных точек данных путём измерения локального отклонения данной точки с учётом её соседей^[1].

Имеет общие концепции с DBSCAN и OPTICS, такие как понятия «основное расстояние» и «достижимое расстояние»^[2], которые используются для оценки локальной плотности^[3].

Локальный уровень выброса основывается на концепции локальной плотности, где локальность задаётся ${\displaystyle k}$ ближайшими соседями, расстояния до которых используются для оценки плотности. Путём сравнения локальной плотности объекта с локальной плотностью его соседей можно выделить области с аналогичной плотностью и точки, которые имеют существенно меньшую плотность, чем её соседи. Эти точки считаются выбросами.

Локальная плотность оценивается типичным расстоянием, с которым точка может быть «достигнута» от соседних точек. Определение «расстояния достижимости», используемого в алгоритме, является дополнительной мерой для получения более устойчивых результатов внутри кластеров.

Пусть ${\displaystyle {\mbox{k-distance}}(A)}$ является расстоянием от объекта ${\displaystyle A}$ до k-ого ближайшего соседа. Заметим, что множество k ближайших соседей включает все объекты на этом расстоянии и в случае «узла» может содержать более k объектов. Мы обозначаем множество k ближайших соседей как ${\displaystyle N_{k}(A)}$.

Это расстояние используется для определения достижимого расстояния (англ. reachability-distance):

${\displaystyle {\mbox{reachability-distance}}_{k}(A,B)=\max\{{\mbox{k-distance}}(B),d(A,B)\}}$

Говоря словами, достижимое расстояние объекта ${\displaystyle A}$ из ${\displaystyle B}$ является истинным расстоянием двух объектов. Объекты, которые принадлежат к k ближайшим соседям точки ${\displaystyle B}$ («основные точки» точки ${\displaystyle B}$, см. DBSCAN), считаются находящимися на одинаковом расстоянии для получения более стабильных результатов. Заметим, что это расстояние не является расстоянием в математическом смысле, поскольку оно не симметрично. (Общей ошибкой является применение ${\displaystyle {\mbox{k-distance}}}$ всегда, так что это даёт слегка другой метод, называемый упрощённым методом локального уровня выброса^[4])

Локальная плотность достижимости объекта ${\displaystyle A}$ определяется как

${\displaystyle {\mbox{lrd}}_{k}(A):=1/\left({\frac {\sum _{B\in N_{k}(A)}{\mbox{reachability-distance}}_{k}(A,B)}{|N_{k}(A)|}}\right)}$,

которая является обратным значением среднему расстоянию достижимости объекта ${\displaystyle A}$ из его соседей. Заметим, что это не является средним расстоянием достижимости соседей из точки ${\displaystyle A}$ (которое по определению должно было бы быть ${\displaystyle {\mbox{k-distance}}(A)}$), а является расстоянием, на котором A может быть «достигнуто» из его соседей. С дубликатами точек это значение может стать бесконечным.

Локальные плотности достижимости затем сравниваются с локальными плотностями достижимости соседей

${\displaystyle {\mbox{LOF}}_{k}(A):={\frac {\sum _{B\in N_{k}(A)}{\frac {{\mbox{lrd}}(B)}{{\mbox{lrd}}(A)}}}{|N_{k}(A)|}}={\frac {\sum _{B\in N_{k}(A)}{\mbox{lrd}}(B)}{|N_{k}(A)|}}/{\mbox{lrd}}(A)}$

что есть средняя локальная плотность достижимости соседей, делённая на локальную плотность достижимости самого объекта. Значение, примерно равное ${\displaystyle 1}$, означает, что объект сравним с его соседями (а тогда он не является выбросом). Значение меньше ${\displaystyle 1}$ означает плотную область (которая может быть внутренностью), а значения, существенно большие ${\displaystyle 1}$, свидетельствуют о выбросах.

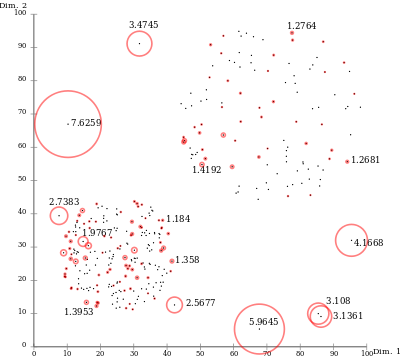
Вследствие локальности подхода алгоритм локального уровня выброса способен выявить выбросы в наборе данных, которые могли бы не быть выбросами в других областях набора данных. Например, точка на «малом» расстоянии до любого плотного кластера является выбросом, в то время как точка внутри редкого кластера может иметь похожие расстояния с её соседями.

В то время как геометрическая интуиция алгоритма применима только к векторным пространствам низкой размерности, алгоритм может быть применён в любом контексте, где функция непохожести может быть определена. Экспериментально было показано, что алгоритм хорошо работает в большом числе ситуаций, часто превосходя соперников, например в системах обнаружения вторжений^[5] и на обработанных классификационных данных ^[6].

Семейство методов локального уровня выброса может быть легко обобщено и затем применено к различным другим задачам, таким как выявление выбросов в географических данных, видеопотоках или сетях ссылок на авторство^[4].

Получающиеся значения трудно интерпретировать. Значение 1 или даже меньше единицы говорит, что точка чисто внутренняя, но нет никакого ясного правила, по которому точка будет выбросом. В одном наборе данных значение 1,1 может уже означать выбросом, в другом наборе данных и параметризации (с сильными локальными флуктуациями) значение 2 может ещё означать внутренность. Эти различия могут случаться внутри одного набора данных ввиду локальности метода. Существуют расширения метода, которые пытаются улучшить алгоритм:

• Бэггинг признаков для обнаружения обособленностей^[7] выполняет алгоритм локального уровня выброса на нескольких проекциях и комбинирует результаты для улучшенного качества обнаружения в высоких размерностях. Это первый подход на основе ансамблевого обучения для обнаружения обособления^[8].
• Локальная вероятность выброса (ЛВВ, англ. Local Outlier Probability, LoOP)^[9] является методом, полученным из метода локального уровня выброса, но использующий экономную локальную статистику, чтобы сделать метод менее чувствительным к выбору параметра k. Кроме того, результирующие значения масштабируются к значению ${\displaystyle [0:1]}$.
• Интерпретация и Унификация Степени Выброса (англ. Interpreting and Unifying Outlier Scores)^[10] предполагает нормализацию оценки выброса к интервалу ${\displaystyle [0:1]}$ с помощью статистического масштабирования с целью увеличения удобства использования и можно рассматривать алгоритм как улучшенную версию идеи локальной вероятности выброса.
• Оценка распределения выбросов и степени выброса (англ. On Evaluation of Outlier Rankings and Outlier Scores)^[11] предлагает средства измерения похожести и отличия методов для построения продвинутого ансамбля методов выявления выбросов с помощью вариантов алгоритма локального уровня выброса и других алгоритмов и улучшения подхода бэггинга признаков.
• Пересмотренное локальное выявление выбросов: обобщённый взгляд на локальность с приложениями в пространственное выявление выбросов, в выявлении выбросов в видео и сетях^[4] обсуждает общую схему в различных методах локального выявления выбросов (включая алгоритм локального уровня выброса, его упрощённую версию и ЛЛВ) и переводит рассмотрение в общие принципы. Эти принципы применяются затем, например, к выявлению выбросов в географических данных, видеопотоках и сети ссылок на авторство.

• Breunig M. M., Kriegel H.-P., Ng R. T., Sander J. R. LOF: Identifying Density-based Local Outliers // Proceedings of the 2000 ACM SIGMOD International Conference on Management of Data. — 2000. — (SIGMOD). — ISBN 1-58113-217-4. — doi:10.1145/335191.335388.
• Breunig M. M., Kriegel H.-P., Ng R. T., Sander J. R. OPTICS-OF: Identifying Local Outliers // Principles of Data Mining and Knowledge Discovery. — 1999. — Т. 1704. — (Lecture Notes in Computer Science). — ISBN 978-3-540-66490-1. — doi:10.1007/978-3-540-48247-5_28.
• Lazarevic A., Ozgur A., Ertoz L., Srivastava J., Kumar V. A comparative study of anomaly detection schemes in network intrusion detection // Proc. 3rd SIAM International Conference on Data Mining. — 2003. Архивная копия от 17 июля 2013 на Wayback Machine
• Guilherme Campos, Arthur Zimek, Jörg Sander, Ricardo J. G. B. Campello, Barbora Micenková, Erich Schubert, Ira Assent, Michael E. Houle. On the evaluation of unsupervised outlier detection: measures, datasets, and an empirical study // Data Mining and Knowledge Discovery. — 2016. — ISSN 1384-5810. — doi:10.1007/s10618-015-0444-8.
• Lazarevic A., Kumar V. Feature bagging for outlier detection // Proc. 11th ACM SIGKDD international conference on Knowledge Discovery in Data Mining. — 2005. — doi:10.1145/1081870.1081891.
• Zimek A., Campello R. J. G. B., Sander J. R. Ensembles for unsupervised outlier detection // ACM SIGKDD Explorations Newsletter. — 2014. — Т. 15. — doi:10.1145/2594473.2594476.
• Kriegel H.-P., Kröger P., Schubert E., Zimek A. LoOP: Local Outlier Probabilities // Proceedings of the 18th ACM conference on Information and knowledge management. — 2009. — ISBN 978-1-60558-512-3. — doi:10.1145/1645953.1646195.
• Kriegel H.-P., Kröger P., Schubert E., Zimek A. Interpreting and Unifying Outlier Scores // Proceedings of the 2011 SIAM International Conference on Data Mining. — 2011. — ISBN 978-0-89871-992-5. — doi:10.1137/1.9781611972818.2.
• Schubert E., Wojdanowski R., Zimek A., Kriegel H. P. On Evaluation of Outlier Rankings and Outlier Scores // Proceedings of the 2012 SIAM International Conference on Data Mining. — 2012. — ISBN 978-1-61197-232-0. — doi:10.1137/1.9781611972825.90.
• Schubert E., Zimek A., Kriegel H. -P. Local outlier detection reconsidered: A generalized view on locality with applications to spatial, video, and network outlier detection // Data Mining and Knowledge Discovery. — 2012. — doi:10.1007/s10618-012-0300-z.

Для улучшения этой статьи желательно: Проверить качество перевода с иностранного языка. Исправить статью согласно стилистическим правилам Википедии. После исправления проблемы исключите её из списка. Удалите шаблон, если устранены все недостатки.