Geometri - Vikipedi

Geometri
Bir düzleme, bir kürenin yansıtılması
Ana hatları Tarihi
Dalları Öklidsel Öklid dışı Eliptik Küresel Hiperbolik Tasarı Sentetik Analitik Cebirsel Aritmetik Diyofant Diferansiyel Riemannian Semplektik Ayrık diferansiyel Karmaşık Sonlu Ayrık/Kombinatoryal Dijital Konveks Hesaplamalı Fraktal
Kavramlar Özellikler Boyut Pergel ve çizgilik çizimleri Açı Eğri Köşegen Ortogonalite (Dik) Paralel Köşenokta Eşleşik Benzerlik Simetri
Sıfır boyutlu Nokta
Bir boyutlu Doğru parçası ışın Uzunluk
İki boyutlu Düzlem Alan Çokgen Üçgen Yükseklik Hipotenüs Pisagor teoremi Paralelkenar Kare Dikdörtgen Eşkenar dörtgen Romboid Dörtgen Yamuk Deltoid (geometri) Çember Çap Çevre Alan
Üç boyutlu Hacim Küp Küboid Silindir Piramit Küre
Dört ve üzeri boyutlu Tesseract Hiperküre
Geometriciler
İsme göre Aida Aryabhata Ahmes Apollonius Arşimet Atiyah Baudhayana Bolyai Brahmagupta Cartan Coxeter Descartes Euler Gauss Gromov Hayyám Hilbert İbn-i Heysem el-İşbîlî Jyeṣṭhadeva Kātyāyana Klein Lobachevsky Manava Minkowski Minggatu Öklid Pascal Pisagor Parameshvara Poincaré Riemann Sakabe Siczi el-Tusi Veblen Virasena Yang Hui Zhang Geometricilerin listesi
Döneme göre Milattan önce Ahmes Baudhayana Manava Pisagor Öklid Arşimet Apollonius MS 1–1400'lar Zhang Kātyāyana Aryabhata Brahmagupta Virasena İbn-i Heysem Siczi Hayyám el-İşbîlî el-Tusi Yang Hui Parameshvara 1400'lar–1700'ler Jyeṣṭhadeva Descartes Pascal Minggatu Euler Sakabe Aida 1700'ler–1900'lar Gauss Lobachevsky Bolyai Riemann Klein Poincaré Hilbert Minkowski Cartan Veblen Coxeter Günümüz Atiyah Gromov
g t d

Geometri (eski adı Hendese), matematiğin uzamsal ilişkiler ile ilgilenen alt dalıdır. Yunanca Γεωμετρία "Geo" (yer) ve "metro" (ölçüm) birleşiminden türetilmiş bir isimdir.

Geometri, arazi ölçümü sözcüklerinden türetilmiştir. Herodot (M.Ö. 450), geometrinin başlangıç yerinin Mısır olduğunu kabul eder. Ona göre geometri kavramı Mısır kö­kenlidir. Sözcüğün kullanımı da Eflatun, Aristo ve Thales'e kadar gider. Yalnız Öklid, geometri sözcüğü yerine Elements sözcüğünü yeğlemiştir. Elements sözcüğünün Yunanca karşılığı stoicheia sözcüğüdür.

Bir kümenin üzerine konan ve kümenin ögelerini birbirleriyle ilişkilendiren bir uygun yapı, geometri yapılmasını olanaklı kılar. Bir düzlemin üzerine doğal olarak konacak ve sezgisel uzaklık duygusunu gözetecek "lise geometrisi"nin adı Öklid geometrisidir. Bu geometrinin tarihsel olarak ilginç ve önemli bir özelliği paralellik aksiyomudur. Bu aksiyomu sağlamayan ama geri kalan tüm aksiyomları sağlayan geometrilere Öklid dışı geometriler denir. Bunlara örnek olarak Hiperbolik geometri ya da küresel geometri verilebilir. Ayrıca ölçeksiz bir cetvel, üçgen ve pergelden başka bir şey kullanmadan çalışılan ölçü dışı geometri de vardır.

Günümüzde kullanılan doğru, yay, ışın, açı ortay, kenarortay gibi birçok temel geometri teriminin Türkçesi Mustafa Kemal Atatürk'ün Geometri adlı eserinde yazılan eserde önerdiği terimlerden yararlanılarak kullanılmaya başlanmıştır.

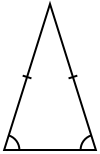
İlk geometrilerin tümü, kendi doğası nedeniyle sezgiseldir. Bunlar daha çok ilk insanların çevresinde görünen doğal şekillerdir. Bu geometriler daha çok görsel tür­dedir. İkinci olarak şekillerin ölçülmesi aşaması gelir. Dörtgenlerin ve üçgenlerin ölçül­mesi ilk kez Mısır'da Ahmes'in (M.Ö. 1550) papirüsünde görülür.

Bu papirüs M.Ö. 1580 tarihinden önce yazılmıştır, b tabanlı ve h yükseklikli ikiz kenar üçgenin alanının bh/2 olduğu verilmiştir.

${\displaystyle {\frac {h.b}{2}}=A(ABC)}$

Yine aynı papirüste d çaplı bir dairenin alanının (d-d/9)2yazımına eş değer olduğu yazılmıştır. Bu yazımlara göre pi sayısı yaklaşık olarak 3,1605 dolay­larındadır. Bu formül geometrik şekilden yaklaşık olarak elde edilmiştir.

${\displaystyle \ A=\pi r^{2}}$

Bu formülün tabletlerde de olduğu söylenmektedir. Çin'in yerli geometrisi de gelişkin örnekler içerir. M.Ö. 1100 yıllarında yazıldığı sanılan Çinlilerin ünlü Nine Sections (Do­kuz Bölüm) kitabında dik açılı üçgen ve ispatsız olarak Pisagor teoremi vardır. Daha sonraki Çin geometrilerinde ölçümleri içeren çok zeki buluşlar vardır. Yine geometrik görünümle Pisagor teoreminin ispatı yapılmıştır. Bu geometrik şekille verilen kitabın M.Ö. 2000 yıllarında yazıldığı sanılıyor.

Hintlerin yerli geometrilerinde de matematiksel bir ispat yoktur. Daha çok görsel ve deneysel ölçülere dayanan kuralları vardır. Bunlar da o kadar ileri bir geometri oluş­turmaz. Bin yıllık bir süre boyunca kullanılan Yunan geometrisi ise daha çok görseldir. Eski Roma geometrisi daha çok kullanım alanlarına yöneliktir.

Arazi ölçümleri, şehir yerleşimleri, su kanalları ve savaş sanatında geometriyi Romalılar iyi kullanmışlardır. Fakat bunlar görsel geometriyi fazla kullanmamışlardır. Zaten görsel geometrinin kökeni Yunanistan'da başlamıştır. Bu çalışmalar ilk kez Thales'in (M.Ö. 600) yapıtlarında görülür. Thales bu teoremleri Mezopotamya'da ve Mısır'da kullandıklarını görür. Altı teoremle önderlik eder ve bu teoremlerin ispatını yapar. Matematikte ispat yapma Thales'le başlamıştır. Thales'in bu ispatları zamanla kaybol­muş ama ondan sonra bunları öğrenenler gelecek kuşaklara aktarmıştır. Bin yıl süren bu görsel Yunan geometrisi zamanla gerilemiş ve yeni bir çalışma getirilmemiştir.

Batı Avrupa'nın uyanmasından önceki yüzyıla kadar Yunan kültürünü ve geomet­risini tam olarak Müslümanlar anlamıştır. Yunan klasiklerini, geometrilerini, fen bilimlerini ve felsefelerini Arapçaya çevirmişlerdir. Fakat ne Öklid'in ne de Apollonius'un çalış­malarına gözle görünür bir katkı yapmışlardır. Okullaşma olma­dığı için gelecek gençlere bu çeviriler öğretilmemiş, bu kitaplar sadece neredeyse bir süs olarak sarayda kalmıştır. Yaptıkları hizmet, kaybolmaya yüz tutmuş Yunan klasiklerini, matematiksel üretimini ve düşüncelerini Arapça çevirileriyle Avrupa'ya iletmişlerdir.

Avrupa'daki karanlık çağda biri Boethius'un (M.Ö. 510) diğeri de Öklid'in (M.Ö. 300) Sements isimli kitabı vardı. Bunlardan sonra Gerbert'in (1000) ve Fibonacci'nin (1202) geometrileri sayılabilir ama bu geometriler İskenderiye geometrilerinden ileri bir dü­zeyde değildi. Avrupa'nın geometrisine büyük katkı 1242 yılında ilk baskısı yapılan Öklid geometrisi oldu. Zaten çok iyi düzenlenmiş ve yazılmış olan bu geometriler Avrupa'ya hızla yayıldı ve her tarafında bilinir oldu. Öklid'in geometrisinin ardından yavaş yavaş geometri ürünleri ortaya çıkmaya başladı. On yedinci yüzyılın başlarında analitik geo­metri ve 1639 yılında da Desargues'ın (1593-1662) izdüşüm geometrisi basıldı. Ana­litik geometri Descartes (1596-1650) ve Fermat (1601-1665) tarafından aynı dönem­lerde yapıldı. Fermat yaptığı çalışmaları yayınlamadığı için analitik geometrinin bulun­ması onuru Descartes'e verildi. Analitik geometri kısaca geometri ile cebir arasındaki ilişkidir diyebiliriz. Geometri ile cebir arasındaki ilişkiyi ilk kez Descartes çıkar­dığı için büyük bir matematikçi olmuştur. Desargues'ın izdüşüm geometrisi matematikçilerin dikkatini çekmiş ve on dokuzuncu yüzyılda çıkacak olan geometricilere coşku ve esin kaynağı olmuştur.

Analitik geometri bulunduktan sonra Apollonius'un (M.Ö. 262-190) konikleri sen­tetik ve analitik olarak yeniden incelenmiştir. Sadece konikler değil, eski Yunan geo­metrisi yeniden analitik olarak gözden geçirilmiştir. Sentetik geometrinin tüm problemleri bir kez de analitik olarak kanıtlanmıştır.

Geometri günlük yaşamın hemen her alanında gereklidir. Geometride uzunluk, alan, hacim, yüzey, açı gibi kavramlar bazı nicelikleri belirlemede kullanılır.

Geometrinin en çok iç içe olduğu dallar; cebir ve trigonometri, mimarlık, mühendislikler (Yol, köprü, yapı, makine, gemi ve uçak yapımı; maden, su ve elektrik işleri gibi bayındırlık ve zanaatla ilgili teknik çalışmalar vb.), endüstriyel alanlar, simülasyonlar, bilgisayar programları ve grafikleri, sibernetik, tasarım, sanat vb.dir. Geometrinin kullanılmadığı meslek ya da alan yok gibidir desek yerinde olur.

Sanat eserlerinin geometrik olması onlara estetik değerler kazandırmıştır. Ünlü ressam Leonardo da Vinci’nin resimde vücut oranları üzerine yaptığı çalışmalar, çizdiği eskizler bulunmaktadır. Bu orana Altın Oran denmektedir.