斯特灵数 - 维基百科，自由的百科全书

在數學中，史特靈數用於解決各種數學分析和組合數學問題，史特靈數是兩組不同的數，均是18世紀由詹姆士·史特靈（英语：James Stirling (mathematician)）引入並以其命名，以第一類史特靈數（英语：Stirling numbers of the first kind）和第二類史特靈數（英语：Stirling numbers of the second kind）的稱呼區分。此外，有時候也將拉赫數（英语：Lah number）稱爲第三類史特靈數^[1]。

第一類史特靈數（英语：Stirling numbers of the first kind）可以定義爲對應遞降階乘展開式的各項係數，即 $${\displaystyle (x)_{n}=\sum _{k=0}^{n}s(n,k)x^{k}\,}$$ 其中，${\displaystyle s(n,k)\,}$（${\displaystyle 0\leq k\leq n\,}$）即爲第一類史特靈數。例如：

$${\displaystyle (x)_{3}=x(x-1)(x-2)\,}$$

則

$${\displaystyle (x)_{3}=0\cdot x^{0}+2\cdot x-3\cdot x^{2}+1\cdot x^{3}\,}$$

於是${\displaystyle s(3,0)=0\,}$， ${\displaystyle s(3,1)=2\,}$， ${\displaystyle s(3,2)=-3\,}$， ${\displaystyle s(3,3)=1\,}$。

由此可知，${\displaystyle s(n,k)\,}$是代數數，或稱爲有符號（第一類）史特靈數（英語：signed Stirling numbers of the first kind）。

有符號史特靈數的絕對值${\displaystyle |s(n,k)|\,}$可以看作（或直接定義爲）把${\displaystyle n\,}$個元素排列成${\displaystyle k\,}$個非空圓圈（循環排列）的方法數目。所以${\displaystyle |s(n,k)|\,}$是算術數，或稱爲無符號（第一類）史特靈數（英語：unsigned Stirling numbers of the first kind）。無符號史特靈數一般可以記爲${\displaystyle c(n,k)\,}$或${\displaystyle \left[{\begin{matrix}n\\k\end{matrix}}\right]\,}$。例如：把${\displaystyle 1\,}$，${\displaystyle 2\,}$，${\displaystyle 3\,}$三個數排列成${\displaystyle 0\,}$個非空圓圈，顯然有零種方法；排列成${\displaystyle 1\,}$個非空圓圈，有${\displaystyle \left({\begin{matrix}&1&\\2&&3\end{matrix}}\right)\,}$，${\displaystyle \left({\begin{matrix}&1&\\3&&2\end{matrix}}\right)\,}$兩種方法；排列成${\displaystyle 2\,}$個非空圓圈，有${\displaystyle \left({\begin{matrix}1\end{matrix}}\right)\,}$${\displaystyle \left({\begin{matrix}2&3\end{matrix}}\right)\,}$，${\displaystyle \left({\begin{matrix}1&2\end{matrix}}\right)\,}$${\displaystyle \left({\begin{matrix}3\end{matrix}}\right)\,}$和${\displaystyle \left({\begin{matrix}1&3\end{matrix}}\right)\,}$${\displaystyle \left({\begin{matrix}2\end{matrix}}\right)\,}$三種方法；排列成${\displaystyle 3\,}$個非空圓圈，有${\displaystyle \left({\begin{matrix}1\end{matrix}}\right)\,}$${\displaystyle \left({\begin{matrix}2\end{matrix}}\right)\,}$${\displaystyle \left({\begin{matrix}3\end{matrix}}\right)\,}$一種方法，所以${\displaystyle \left[{\begin{matrix}3\\0\end{matrix}}\right]=0\,}$${\displaystyle \left[{\begin{matrix}3\\1\end{matrix}}\right]=2\,}$，${\displaystyle \left[{\begin{matrix}3\\2\end{matrix}}\right]=3\,}$，${\displaystyle \left[{\begin{matrix}3\\3\end{matrix}}\right]=1\,}$。可以看到這和前面有符號史特靈數${\displaystyle s(n,k)\,}$在${\displaystyle n=3\,}$時的結果一致（只是符號差異）。

與有符號史特靈數類似，無符號史特靈數可以定義爲對應遞進階乘展開式的各項係數，即

$${\displaystyle (x)^{\overline {n}}=\sum _{k=0}^{n}\left[{\begin{matrix}n\\k\end{matrix}}\right]x^{k}\,}$$

其中，${\displaystyle \left[{\begin{matrix}n\\k\end{matrix}}\right]\,}$（${\displaystyle 0\leq k\leq n\,}$）即爲無符號史特靈數。不過要注意，這裏的記號${\displaystyle \left[{\begin{matrix}n\\k\end{matrix}}\right]\,}$有時候會用來表示高斯二项式系数。

有符號史特靈數和無符號史特靈數有如下關係：

$${\displaystyle s(n,k)=(-1)^{n-k}\left[{\begin{matrix}n\\k\end{matrix}}\right]\,}$$

無符號史特靈數有更多的應用。例如，將${\displaystyle n\,}$個元素分成${\displaystyle k\,}$組，每組內的元素再進行排列的方法數目即可用無符號史特靈數${\displaystyle \left[{\begin{matrix}n\\k\end{matrix}}\right]\,}$求得。以${\displaystyle \left[{\begin{matrix}4\\2\end{matrix}}\right]=11\,}$爲例：

1. (A,B)(C,D)
2. (A,C)(B,D)
3. (A,D)(B,C)
4. (A)(B,C,D)
5. (A)(B,D,C)
6. (B)(A,C,D)
7. (B)(A,D,C)
8. (C)(A,B,D)
9. (C)(A,D,B)
10. (D)(A,B,C)
11. (D)(A,C,B)

或用有向圖^{[來源請求]}表示如下：

無符號史特靈數有如下遞推關係式：

$${\displaystyle \left[{\begin{matrix}n+1\\k\end{matrix}}\right]=n\left[{\begin{matrix}n\\k\end{matrix}}\right]+\left[{\begin{matrix}n\\k-1\end{matrix}}\right]\,}$$

其中，${\displaystyle k>0}$，且初始條件爲 ${\displaystyle \left[{\begin{matrix}0\\0\end{matrix}}\right]=1\,}$，${\displaystyle \left[{\begin{matrix}n\\0\end{matrix}}\right]=\left[{\begin{matrix}0\\n\end{matrix}}\right]=0\,}$（${\displaystyle n>0}$）。

有符號史特靈數有如下遞推關係式：

$${\displaystyle s(n+1,k)=-ns(n,k)+s(n,k-1)}$$

下表其實是一部分無符號史特靈數，要想獲得有符號史特靈數，可以通過它們之間的關係式：

$${\displaystyle s(n,k)=(-1)^{n-k}\left[{\begin{matrix}n\\k\end{matrix}}\right]\,}$$

求得。

k n	0	1	2	3	4	5	6
0	1
1	0	1
2	0	1	1
3	0	2	3	1
4	0	6	11	6	1
5	0	24	50	35	10	1
6	0	120	274	225	85	15	1

觀察前面的“第一類史特靈數表”，我們可以得到一些簡單的性質：

${\displaystyle \left[{\begin{matrix}0\\0\end{matrix}}\right]=1\,}$，${\displaystyle \left[{\begin{matrix}n\\0\end{matrix}}\right]=0\,}$（${\displaystyle n>0\,}$）。

如果${\displaystyle k>0\,}$，我們有

${\displaystyle \left[{\begin{matrix}0\\k\end{matrix}}\right]=0\,}$；

或更一般地，如果${\displaystyle k>n\,}$，我們有

${\displaystyle \left[{\begin{matrix}n\\k\end{matrix}}\right]=0\,}$。

還有

${\displaystyle \left[{\begin{matrix}n\\1\end{matrix}}\right]=(n-1)!\,}$，

${\displaystyle \left[{\begin{matrix}n\\n\end{matrix}}\right]=1\,}$，

${\displaystyle \left[{\begin{matrix}n\\n-1\end{matrix}}\right]={n \choose 2}\,}$，

${\displaystyle \left[{\begin{matrix}n\\n-2\end{matrix}}\right]={\frac {1}{4}}(3n-1){n \choose 3}\,}$，

${\displaystyle \left[{\begin{matrix}n\\n-3\end{matrix}}\right]={n \choose 2}{n \choose 4}\,}$。

注：這裏記號${\displaystyle {n \choose k}\,}$表示组合数。

第二類史特靈數（英语：Stirling numbers of the second kind）與第一類史特靈數類似，可以用遞降階乘定義爲

$${\displaystyle x^{n}=\sum _{k=0}^{n}\left\{{\begin{matrix}n\\k\end{matrix}}\right\}(x)_{k}\,}$$

其中，${\displaystyle \left\{{\begin{matrix}n\\k\end{matrix}}\right\}\,}$^[2][3]即爲第二類史特靈數，也可以記爲${\displaystyle S(n,k)\,}$^[4]。例如：

$${\displaystyle x^{3}=\left\{{\begin{matrix}3\\0\end{matrix}}\right\}(x)_{0}+\left\{{\begin{matrix}3\\1\end{matrix}}\right\}(x)_{1}+\left\{{\begin{matrix}3\\2\end{matrix}}\right\}(x)_{2}+\left\{{\begin{matrix}3\\3\end{matrix}}\right\}(x)_{3}\,}$$

即

$${\displaystyle x^{3}=\left\{{\begin{matrix}3\\0\end{matrix}}\right\}+\left\{{\begin{matrix}3\\1\end{matrix}}\right\}x+\left\{{\begin{matrix}3\\2\end{matrix}}\right\}x(x-1)+\left\{{\begin{matrix}3\\3\end{matrix}}\right\}x(x-1)(x-2)\,}$$

將遞降階乘展開並合併同類項，得

$${\displaystyle x^{3}=\left\{{\begin{matrix}3\\0\end{matrix}}\right\}+\left(\left\{{\begin{matrix}3\\1\end{matrix}}\right\}-\left\{{\begin{matrix}3\\2\end{matrix}}\right\}+2\left\{{\begin{matrix}3\\3\end{matrix}}\right\}\right)x+\left(\left\{{\begin{matrix}3\\2\end{matrix}}\right\}-3\left\{{\begin{matrix}3\\3\end{matrix}}\right\}\right)x^{2}+\left\{{\begin{matrix}3\\3\end{matrix}}\right\}x^{3}\,}$$

比較等式兩邊係數，得

$${\displaystyle {\begin{cases}\left\{{\begin{matrix}3\\0\end{matrix}}\right\}=0\\\left\{{\begin{matrix}3\\1\end{matrix}}\right\}-\left\{{\begin{matrix}3\\2\end{matrix}}\right\}+2\left\{{\begin{matrix}3\\3\end{matrix}}\right\}=0\\\left\{{\begin{matrix}3\\2\end{matrix}}\right\}-3\left\{{\begin{matrix}3\\3\end{matrix}}\right\}=0\\\left\{{\begin{matrix}3\\3\end{matrix}}\right\}=1\end{cases}}\,}$$

解得

${\displaystyle \left\{{\begin{matrix}3\\0\end{matrix}}\right\}=0\,}$，${\displaystyle \left\{{\begin{matrix}3\\1\end{matrix}}\right\}=1\,}$，${\displaystyle \left\{{\begin{matrix}3\\2\end{matrix}}\right\}=3\,}$，${\displaystyle \left\{{\begin{matrix}3\\3\end{matrix}}\right\}=1\,}$。

第二類史特靈數計算的是將含有${\displaystyle n\,}$個元素的集合拆分爲${\displaystyle k\,}$個非空子集的方法數目^[5]。例如：對於集合${\displaystyle \left\{1,2,3\right\}\,}$，若拆分爲${\displaystyle 0\,}$個非空子集，顯然有零種方法；拆分爲${\displaystyle 1\,}$個非空子集，只有${\displaystyle \left\{1,2,3\right\}\,}$一種方法；拆分爲${\displaystyle 2\,}$個非空子集，有${\displaystyle \left\{1\right\}\,}$${\displaystyle \left\{2,3\right\}\,}$，${\displaystyle \left\{1,2\right\}\,}$${\displaystyle \left\{3\right\}\,}$，${\displaystyle \left\{2\right\}\,}$${\displaystyle \left\{1,3\right\}\,}$三種方法；拆分爲${\displaystyle 3\,}$個非空子集，有${\displaystyle \left\{1\right\}\,}$${\displaystyle \left\{2\right\}\,}$${\displaystyle \left\{3\right\}\,}$一種方法。於是${\displaystyle \left\{{\begin{matrix}3\\0\end{matrix}}\right\}=0\,}$，${\displaystyle \left\{{\begin{matrix}3\\1\end{matrix}}\right\}=1\,}$，${\displaystyle \left\{{\begin{matrix}3\\2\end{matrix}}\right\}=3\,}$，${\displaystyle \left\{{\begin{matrix}3\\3\end{matrix}}\right\}=1\,}$。

第二類史特靈數可以使用以下公式進行計算：^[6]

$${\displaystyle \left\{{\begin{matrix}n\\k\end{matrix}}\right\}={\frac {1}{k!}}\sum _{i=0}^{k}(-1)^{i}\left({\begin{matrix}k\\i\end{matrix}}\right)(k-i)^{n}\,}$$

取${\displaystyle \left\{{\begin{matrix}3\\2\end{matrix}}\right\}\,}$進行驗算，有

$${\displaystyle \left\{{\begin{matrix}3\\2\end{matrix}}\right\}={\frac {1}{2!}}\sum _{i=0}^{2}(-1)^{i}\left({\begin{matrix}2\\i\end{matrix}}\right)(2-i)^{3}\,}$$

即

$${\displaystyle \left\{{\begin{matrix}3\\2\end{matrix}}\right\}={\frac {1}{2}}\left(\left({\begin{matrix}2\\0\end{matrix}}\right)\times 2^{3}-\left({\begin{matrix}2\\1\end{matrix}}\right)\times 1^{3}+\left({\begin{matrix}2\\2\end{matrix}}\right)\times 0^{3}\right)\,}$$

於是

$${\displaystyle \left\{{\begin{matrix}3\\2\end{matrix}}\right\}={\frac {1}{2}}\left(1\times 8-2\times 1+1\times 0\right)=3\,}$$

將${\displaystyle n\,}$個人分成${\displaystyle k\,}$組的分組方法的數目。例如有甲、乙、丙、丁四人，若所有人分成${\displaystyle 1\,}$組，只能所有人在同一組，因此${\displaystyle \left\{{\begin{matrix}4\\1\end{matrix}}\right\}=1\,}$；若所有人分成${\displaystyle 4\,}$組，只能每人獨立一組，因此${\displaystyle \left\{{\begin{matrix}4\\4\end{matrix}}\right\}=1\,}$；若分成${\displaystyle 2\,}$組，可以是甲乙一組、丙丁一組，或甲丙一組、乙丁一組，或甲丁一組、乙丙一組，或其中三人同一組另一人獨立一組，即：

1. {甲, 乙}{丙, 丁}
2. {甲, 丙}{乙,丁}
3. {甲, 丁}{乙, 丙}
4. {甲}{乙, 丙, 丁}
5. {乙}{甲, 丙, 丁}
6. {丙}{甲, 乙, 丁}
7. {丁}{甲, 乙, 丙}

因此${\displaystyle \left\{{\begin{matrix}4\\2\end{matrix}}\right\}=7\,}$。同理，可以得到${\displaystyle \left\{{\begin{matrix}4\\3\end{matrix}}\right\}=6\,}$。

第二類史特靈數有與第一類史特靈數類似的遞推關係式：

$${\displaystyle \left\{{\begin{matrix}n+1\\k\end{matrix}}\right\}=k\left\{{\begin{matrix}n\\k\end{matrix}}\right\}+\left\{{\begin{matrix}n\\k-1\end{matrix}}\right\}\,}$$

其中，${\displaystyle k>0}$，且初始條件爲 ${\displaystyle \left\{{\begin{matrix}0\\0\end{matrix}}\right\}=1\,}$，${\displaystyle \left\{{\begin{matrix}n\\0\end{matrix}}\right\}=\left\{{\begin{matrix}0\\n\end{matrix}}\right\}=0\,}$（${\displaystyle n>0}$）。

下面爲部分第二類史特靈數：

k n	0	1	2	3	4	5	6
0	1
1	0	1
2	0	1	1
3	0	1	3	1
4	0	1	7	6	1
5	0	1	15	25	10	1
6	0	1	31	90	65	15	1

觀察前面的“第二類史特靈數表”，我們可以得到一些簡單的性質：

${\displaystyle \left\{{\begin{matrix}0\\0\end{matrix}}\right\}=1\,}$，${\displaystyle \left\{{\begin{matrix}n\\0\end{matrix}}\right\}=0\,}$（${\displaystyle n>0\,}$）。

如果${\displaystyle k>0\,}$，我們有

${\displaystyle \left\{{\begin{matrix}0\\k\end{matrix}}\right\}=0\,}$；

或更一般地，如果${\displaystyle k>n\,}$，我們有

${\displaystyle \left\{{\begin{matrix}n\\k\end{matrix}}\right\}=0\,}$。

還有

${\displaystyle \left\{{\begin{matrix}n\\1\end{matrix}}\right\}=1\,}$，

${\displaystyle \left\{{\begin{matrix}n\\2\end{matrix}}\right\}=2^{n-1}-1\,}$，

${\displaystyle \left\{{\begin{matrix}n\\3\end{matrix}}\right\}={\frac {1}{2}}(3^{n-1}+1)-2^{n-1}\,}$，

${\displaystyle \left\{{\begin{matrix}n\\n\end{matrix}}\right\}=1\,}$，

${\displaystyle \left\{{\begin{matrix}n\\n-1\end{matrix}}\right\}={n \choose 2}\,}$，

${\displaystyle \left\{{\begin{matrix}n\\n-2\end{matrix}}\right\}={n \choose 3}+3{n \choose 4}\,}$，

${\displaystyle \left\{{\begin{matrix}n\\n-3\end{matrix}}\right\}={n \choose 4}+10{n \choose 5}+15{n \choose 6}\,}$。

貝爾數和第二類史特靈數有如下關係：

$${\displaystyle B_{n}=\sum _{k=0}^{n}\left\{{\begin{matrix}n\\k\end{matrix}}\right\}\,}$$

第一類和第二類史特靈數可以看作互爲逆矩陣的關係：

$${\displaystyle \sum _{j\geq 0}s(n,j)S(j,k)=\sum _{j\geq 0}(-1)^{n-j}{\begin{bmatrix}n\\j\end{bmatrix}}{\begin{Bmatrix}j\\k\end{Bmatrix}}=\delta _{nk}}{\displaystyle \sum _{j\geq 0}s(n,j)S(j,k)=\sum _{j\geq 0}(-1)^{n-j}{\begin{bmatrix}n\\j\end{bmatrix}}{\begin{Bmatrix}j\\k\end{Bmatrix}}=\delta _{nk}\,}$$

以及

$${\displaystyle \sum _{j\geq 0}S(n,j)s(j,k)=\sum _{j\geq 0}(-1)^{j-k}{\begin{Bmatrix}n\\j\end{Bmatrix}}{\begin{bmatrix}j\\k\end{bmatrix}}=\delta _{nk}}{\displaystyle \sum _{j\geq 0}S(n,j)s(j,k)=\sum _{j\geq 0}(-1)^{j-k}{\begin{Bmatrix}n\\j\end{Bmatrix}}{\begin{bmatrix}j\\k\end{bmatrix}}=\delta _{nk}\,}$$

其中，${\displaystyle \delta _{nk}\,}$是克羅內克爾δ。

拉赫數（英语：Lah number）是由伊沃·拉赫（英语：Ivo Lah）在1954年發現的^[7][8]，因爲拉赫數與史特靈數關係密切，所以有時拉赫數也被稱爲第三類史特靈數。可以用遞進階乘和遞降階乘定義爲

$${\displaystyle x^{(n)}=\sum _{k=0}^{n}L(n,k)(x)_{k}\,}$$

或

$${\displaystyle (x)_{n}=\sum _{k=0}^{n}(-1)^{n-k}L(n,k)x^{(k)}\,}$$

其中， ${\displaystyle L(n,k)\,}$即爲拉赫數。例如：

$${\displaystyle x^{(3)}=\sum _{k=0}^{3}L(3,k)(x)_{k}\,}$$

即

${\displaystyle x(x+1)(x+2)=L(3,0)\cdot 1+L(3,1)\cdot x+L(3,2)\cdot x(x-1)+L(3,3)\cdot x(x-1)(x-2)\,}$

等式兩邊展開並合併同類項，得

$${\displaystyle 0\cdot x^{0}+2\cdot x+3\cdot x^{2}+1\cdot x^{3}=L(3,0)+[L(3,1)-L(3,2)+2L(3,3)]\cdot x+[L(3,2)-3L(3,3)]\cdot x^{2}+L(3,3)\cdot x^{3}\,}$$

比較等式兩邊係數，得

$${\displaystyle {\begin{cases}{L(3,0)=0}\\{L(3,1)-L(3,2)+2L(3,3)=2}\\{L(3,2)-3L(3,3)=3}\\{L(3,3)=1}\end{cases}}\,}$$

解得 ${\displaystyle L(3,0)=0\,}$，${\displaystyle L(3,1)=6\,}$， ${\displaystyle L(3,2)=6\,}$，${\displaystyle L(3,3)=1\,}$。

或

$${\displaystyle (x)_{3}=\sum _{k=0}^{3}(-1)^{3-k}L(3,k)x^{(3)}\,}$$

即

${\displaystyle x(x-1)(x-2)=L(3,0)\cdot 1+L(3,1)\cdot x+L(3,2)\cdot x(x+1)+L(3,3)\cdot x(x+1)(x+2)\,}$

等式兩邊展開並合併同類項，得

$${\displaystyle 0\cdot x^{0}+2\cdot x-3\cdot x^{2}+1\cdot x^{3}=-L(3,0)+[L(3,1)-L(3,2)+2L(3,3)]\cdot x+[-L(3,2)+3L(3,3)]\cdot x^{2}+L(3,3)\cdot x^{3}\,}$$

比較等式兩邊係數，得

$${\displaystyle {\begin{cases}{L(3,0)=0}\\{L(3,1)-L(3,2)+2L(3,3)=2}\\{-L(3,2)+3L(3,3)=-3}\\{L(3,3)=1}\end{cases}}\,}$$

解得 ${\displaystyle L(3,0)=0\,}$，${\displaystyle L(3,1)=6\,}$， ${\displaystyle L(3,2)=6\,}$，${\displaystyle L(3,3)=1\,}$。

以上定義的拉赫數是無符號拉赫數（英語： signed Lah numbers），有符號拉赫數（英語：signed Lah numbers）的定義如下：

$${\displaystyle x^{(n)}=(-1)^{n}\sum _{k=0}^{n}L(n,k)(x)_{k}\,}$$

或

$${\displaystyle (x)_{n}=\sum _{k=0}^{n}(-1)^{k}L(n,k)x^{(k)}\,}$$

無符號拉赫數計算的是將含有${\displaystyle n\,}$個元素的集合拆分爲${\displaystyle k\,}$個非空線性有序子集的方法數目^[9]。例如：對於集合${\displaystyle \left\{1,2,3\right\}\,}$，若拆分爲${\displaystyle 0\,}$個非空線性有序子集，顯然有零種方法；拆分爲${\displaystyle 1\,}$個非空線性有序子集，有${\displaystyle \left\{(1,2,3)\right\}\,}$，${\displaystyle \left\{(1,3,2)\right\}\,}$，${\displaystyle \left\{(2,1,3)\right\}\,}$，${\displaystyle \left\{(2,3,1)\right\}\,}$，${\displaystyle \left\{(3,1,2)\right\}\,}$，${\displaystyle \left\{(3,2,1)\right\}\,}$六種方法；拆分爲${\displaystyle 2\,}$個非空線性有序子集，有${\displaystyle \left\{(1)\right\}\,}$${\displaystyle \left\{(2,3)\right\}\,}$，${\displaystyle \left\{(1)\right\}\,}$${\displaystyle \left\{(3,2)\right\}\,}$，${\displaystyle \left\{(2)\right\}\,}$${\displaystyle \left\{(1,3)\right\}\,}$，${\displaystyle \left\{(2)\right\}\,}$${\displaystyle \left\{(3,1)\right\}\,}$，${\displaystyle \left\{(3)\right\}\,}$${\displaystyle \left\{(1,2)\right\}\,}$，${\displaystyle \left\{(3)\right\}\,}$${\displaystyle \left\{(2,1)\right\}\,}$六種方法；拆分爲${\displaystyle 3\,}$個非空線性有序子集，有${\displaystyle \left\{(1)\right\}\,}$，${\displaystyle \left\{(2)\right\}\,}$，${\displaystyle \left\{(3)\right\}\,}$一種方法。於是${\displaystyle L(3,0)=0\,}$，${\displaystyle L(3,1)=6\,}$， ${\displaystyle L(3,2)=6\,}$，${\displaystyle L(3,3)=1\,}$。

無符號拉赫數可以使用以下公式進行計算：

$${\displaystyle L(n,k)={n-1 \choose k-1}{\frac {n!}{k!}}\,}$$

有符號拉赫數可以使用以下公式進行計算：

$${\displaystyle L'(n,k)=(-1)^{n}{n-1 \choose k-1}{\frac {n!}{k!}}\,}$$

無符號拉赫數有如下遞推關係：

${\displaystyle L(n,k+1)={\frac {n-k}{k(k+1)}}L(n,k)}$

或

${\displaystyle L(n+1,k)=(n+k)L(n,k)+L(n,k-1)\,}$

其中，${\displaystyle L(n,0)=0\,}$，${\displaystyle L(n,0)=0\,}$，${\displaystyle L(n,k)=0\,}$（${\displaystyle k>n\,}$），${\displaystyle L(1,1)=1\,}$

下面爲部分無符號拉赫數：

k n	0	1	2	3	4	5	6
0	1
1	0	1
2	0	2	1
3	0	6	6	1
4	0	24	36	12	1
5	0	120	240	120	20	1
6	0	720	1800	1200	300	30	1

觀察前面的“拉赫數表”，我們可以得到一些簡單性質：

${\displaystyle L(0,0)=1}$， ${\displaystyle L(n,0)=0}$（${\displaystyle n>0}$）

如果${\displaystyle k>n}$，有 ${\displaystyle L(0,0)=1}$，${\displaystyle L(n,k)=0}$

還有

${\displaystyle L(n,1)=n!}$

${\displaystyle L(n,2)={\frac {(n-1)n!}{2}}}$

${\displaystyle L(n,3)={\frac {(n-2)(n-1)n!}{12}}}$

${\displaystyle L(n,n-1)=n(n-1)}$

${\displaystyle L(n,n)=1}$

${\displaystyle \sum _{n\geq k}L(n,k){\frac {x^{n}}{n!}}={\frac {1}{k!}}\left({\frac {x}{1-x}}\right)^{k}}$

無符號拉赫數計算公式可以作進一步拓展：

${\displaystyle L(n,k)={n-1 \choose k-1}{\frac {n!}{k!}}={n \choose k}{\frac {(n-1)!}{(k-1)!}}={n \choose k}{n-1 \choose k-1}(n-k)!}$

${\displaystyle L(n,k)={\frac {n!(n-1)!}{k!(k-1)!}}\cdot {\frac {1}{(n-k)!}}=\left({\frac {n!}{k!}}\right)^{2}{\frac {k}{n(n-k)!}}}$

無符號拉赫數與兩類史特靈數都有關係^[10]，關係如下：

$${\displaystyle L(n,k)=\sum _{j=0}^{n}\left[{\begin{matrix}n\\j\end{matrix}}\right]\left\{{\begin{matrix}j\\k\end{matrix}}\right\}\,}$$

取${\displaystyle L(3,2)\,}$進行驗算，有

$${\displaystyle L(3,2)=\sum _{j=0}^{3}\left[{\begin{matrix}3\\j\end{matrix}}\right]\left\{{\begin{matrix}j\\2\end{matrix}}\right\}\,}$$

即

$${\displaystyle L(3,2)=\left[{\begin{matrix}3\\0\end{matrix}}\right]\left\{{\begin{matrix}0\\2\end{matrix}}\right\}+\left[{\begin{matrix}3\\1\end{matrix}}\right]\left\{{\begin{matrix}1\\2\end{matrix}}\right\}+\left[{\begin{matrix}3\\2\end{matrix}}\right]\left\{{\begin{matrix}2\\2\end{matrix}}\right\}+\left[{\begin{matrix}3\\3\end{matrix}}\right]\left\{{\begin{matrix}3\\2\end{matrix}}\right\}\,}$$

於是

$${\displaystyle L(3,2)=\left[{\begin{matrix}3\\2\end{matrix}}\right]\left\{{\begin{matrix}2\\2\end{matrix}}\right\}+\left[{\begin{matrix}3\\3\end{matrix}}\right]\left\{{\begin{matrix}3\\2\end{matrix}}\right\}=3\times 1+1\times 3=6\,}$$

由無符號拉赫數與兩類史特靈數之間的關係，考慮到兩類史特靈數之間的關係，有

$${\displaystyle \sum _{j\geq 0}L(n,j)L(j,k)=\delta _{nk}\,}$$

其中，${\displaystyle \delta _{nk}\,}$是克羅內克爾δ。

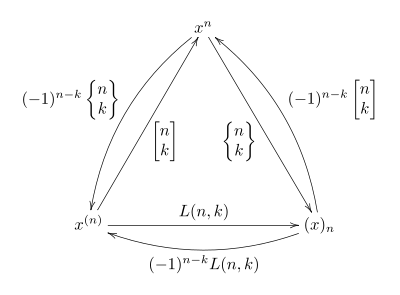
三類史特靈數以及乘方、階乘之間的關係可以用下圖表示：