二項式分布 - 维基百科，自由的百科全书

二項分布

概率质量函數
累積分布函數
记号	${\displaystyle \operatorname {B} (n,p)}$
参数	${\displaystyle n>0}$ ${\displaystyle 0\leq p\leq 1}$
值域	${\displaystyle k\in \{0,\dots ,n\}}$
概率质量函数	${\displaystyle {n \choose k}p^{k}(1-p)^{n-k}}$
累積分布函數	${\displaystyle I_{1-p}(n-\lfloor k\rfloor ,\lfloor k\rfloor +1)}$
期望值	${\displaystyle np}$
中位數	${\displaystyle \lfloor np\rfloor }$或${\displaystyle \lceil np\rceil }$
眾數	${\displaystyle \lfloor (n+1)p\rfloor }$
方差	${\displaystyle np(1-p)}$
偏度	${\displaystyle {\frac {1-2p}{\sqrt {np(1-p)}}}}$
峰度	${\displaystyle {\frac {1-6p(1-p)}{np(1-p)}}}$
熵	${\displaystyle {\frac {1}{2}}\ln \left(2\pi nep(1-p)\right)+O\left({\frac {1}{n}}\right)}$
矩生成函数	${\displaystyle (1-p+pe^{t})^{n}}$
特徵函数	${\displaystyle (1-p+pe^{it})^{n}}$
概率母函数	${\displaystyle (1-p+pz)^{n}}$

在概率论和统计学中，二项分布（英語：binomial distribution）是一种离散概率分布，描述在进行独立随机试验时，每次试验都有相同概率“成功”的情况下，获得成功的总次数。掷硬币十次出现五次正面的概率、产品合格率${\displaystyle \,99\%\,}$时抽出一百件样本没有发现一件次品的概率等等，都可以由二项分布给出。

只有“成功”和“失败”两种可能结果，每次重复时成功概率不变的独立随机试验称作伯努利试验，例如上述的掷硬币出现正面或反面、对产品进行抽样检查时抽到正品或次品。伯努利试验作为理论模型，其前提在现实中无法完全得到满足，比如生产线会磨损，因此每件产品合格的概率并非固定^[1]。尽管如此，二项分布给出的概率通常足以用于提供有用的推断；即使在已知前提没有满足的场合，二项分布也能用于参考和比较。二项分布的应用出现在遗传学、质量控制等领域之中。^[2]

若随机变量${\displaystyle \,X\,}$有概率质量函数

${\displaystyle \Pr(X=k)={n \choose k}p^{k}(1-p)^{n-k}\quad (k=0,1,\ldots ,n),}$

其中${\displaystyle \,n\,}$为正整数、${\displaystyle \,0\leq p\leq 1\,}$，则称${\displaystyle \,X\,}$服从参数为${\displaystyle \,n,p\,}$的二项分布^[3]，记为${\displaystyle \,X\sim \operatorname {B} (n,p)\,}$或${\displaystyle \,X\sim \operatorname {Bin} (n,p)\,}$。习惯上${\displaystyle \,1-p\,}$也用${\displaystyle \,q\,}$表示。^[1]

进行${\displaystyle \,n\,}$次独立伯努利试验的结果可以由${\displaystyle \,n\,}$个字母表示，例如用${\displaystyle \,S\,}$表示成功，${\displaystyle \,F\,}$表示失败，则

${\displaystyle SSFSF}$

表示五次试验中第一、二、四次的结果为成功，其余为失败。设每次试验成功的概率为${\displaystyle \,p\,}$，失败的概率为${\displaystyle \,1-p\,}$。因为试验相互独立，每一种排列${\displaystyle \,k\,}$个${\displaystyle \,S\,}$、${\displaystyle \,n-k\,}$个${\displaystyle \,F\,}$的方式对应的概率为${\displaystyle \,p^{k}(1-p)^{n-k}\,}$。^[1]

从${\displaystyle \,n\,}$个不同元素中选出含${\displaystyle \,k\,}$个元素的子集的方法数量等于二项式系数

${\displaystyle {n \choose k}={\frac {n!}{k!(n-k)!}}.}$^[4]

而每种对${\displaystyle \,k\,}$个${\displaystyle \,S\,}$、${\displaystyle \,n-k\,}$个${\displaystyle \,F\,}$的排列都可理解为从${\displaystyle \,n\,}$个位置中选出${\displaystyle \,k\,}$个作为字母${\displaystyle \,S\,}$的位置的方法，这种方法的数量即为${\displaystyle \,{n \choose k}\,}$。与每种排列方式对应的概率相乘，便得到定义中的概率

${\displaystyle {n \choose k}p^{k}(1-p)^{n-k}.}$^[5]

二项分布是最早得到研究的概率分布之一^[6]。丹麦统计学家安德斯·哈爾德认为其历史可以追溯至布莱兹·帕斯卡与皮埃尔·德·费马于1654年对点数分配问题的讨论：两名玩家赢得每局游戏的机会相同，赢得一定局数的胜者可获得奖金，但比赛仅进行了数局，尚未分出胜负就被迫中断，则奖金该如何分配？帕斯卡认为，奖金的分配应当基于玩家距离胜利所差的局数：若一名玩家还需${\displaystyle \,r\,}$局获胜，另一名玩家还需${\displaystyle \,s\,}$局获胜，则应考虑在${\displaystyle \,r+s-1\,}$局比赛的${\displaystyle \,2^{r+s-1}\,}$种结果中，两名玩家分别在多少种情况中获胜。两人的讨论限于这一问题本身，并未推导出二项分布的概率，但这一解法可被视作基于参数${\displaystyle \,p=1/2\,}$的二项分布。^[7]

对二项分布概率的推导为雅各布·伯努利于《猜度术（英语：Ars Conjectandi）》中作出。该著作在他去世后，于1713年得到出版，被视作概率论的奠基性作品。伯努利还在其中首次给出了弱大数定律的严格证明^[8][9]。对二项分布的正态近似则是由亞伯拉罕·棣莫弗发现，这一工作于1733年完成，于1738年出版在其著作《机遇论（英语：The Doctrine of Chances）》的第二版中。^[10]

参数为${\displaystyle \,n,p\,}$的二项分布的期望值为${\displaystyle \,np\,}$，方差为${\displaystyle \,np(1-p)\,}$。其概率母函数为

${\displaystyle G(z)=(1-p+pz)^{n},}$

矩母函数为

${\displaystyle M_{X}(t)=(1-p+pe^{t})^{n},}$

特征函数为

${\displaystyle \varphi _{X}(t)=(1-p+pe^{it})^{n}.}$^[3][11]

参数${\displaystyle \,n=1\,}$的二项分布称作伯努利分布^[3]。多项分布（英语：Multinomial distribution）是二项分布的拓展，描述重复进行不限于两种结果、可能有多种可能结果的随机试验时的概率^[12]。二项分布本身是超几何分布的极限形式。^[13]

若${\displaystyle \,X_{1},X_{2}\,}$两个随机变量独立，分别服从参数为${\displaystyle \,n_{1},p\,}$和${\displaystyle \,n_{2},p\,}$的二项分布，则${\displaystyle \,X_{1}+X_{2}\,}$即是在${\displaystyle \,n_{1}+n_{2}\,}$次独立伯努利试验中取得成功的次数，所以${\displaystyle \,X_{1}+X_{2}\,}$服从参数为${\displaystyle \,n_{1}+n_{2},p\,}$的二项分布。这一结论亦可通过将两者的概率母函数相乘而得出。在条件${\displaystyle \,X_{1}+X_{2}=k\,}$之下，随机变量${\displaystyle \,X_{1}\,}$的条件概率分布是参数为${\displaystyle \,k,n_{1},n_{1}+n_{2}\,}$的超几何分布。^[14]

计算${\displaystyle \,\Pr(X=k)\,}$和${\displaystyle \,\Pr(X=k+1)\,}$的比值可以得到

${\displaystyle {\frac {\Pr(X=k+1)}{\Pr(X=k)}}={\frac {(n-k)p}{(k+1)(1-p)}}\quad (k=0,1,\ldots ,n-1),}$

因此，当${\displaystyle \,k<(n+1)p-1\,}$时，${\displaystyle \,\Pr(X=k)\,}$随${\displaystyle \,k\,}$增加而上升；当${\displaystyle \,k>(n+1)p-1\,}$时，${\displaystyle \,\Pr(X=k)\,}$随${\displaystyle \,k\,}$增加而下降。故二项分布的众数为${\displaystyle \,(n+1)p\,}$的下取整${\displaystyle \,\lfloor (n+1)p\rfloor \,}$。若${\displaystyle \,(n+1)p\,}$本身是整数，则${\displaystyle \,(n+1)p\,}$和${\displaystyle \,(n+1)p-1\,}$均是众数。若${\displaystyle \,p<(n+1)^{-1}\,}$，则众数为${\displaystyle \,0\,}$。^[15]

二项分布的中位数${\displaystyle \,m\,}$位于${\displaystyle \,np\,}$的上下取整之间，即${\displaystyle \,\lfloor np\rfloor \leq m\leq \lceil np\rceil \,}$；若${\displaystyle \,np\,}$为整数，则中位数${\displaystyle \,m=np\,}$。中位数${\displaystyle \,m\,}$和期望值${\displaystyle \,np\,}$之间的差满足

${\displaystyle |m-np|<\max\{p,1-p\}.}$

若${\displaystyle \,p>\ln 2\,}$或${\displaystyle \,p<1-\ln 2\,}$，则该上界可进一步缩减为

${\displaystyle |m-np|<\ln 2.}$

若${\displaystyle \,n\,}$为奇数、${\displaystyle \,p=1/2\,}$，则${\displaystyle \,(n-1)/2\,}$和${\displaystyle \,(n+1)/2\,}$均为中位数。^[16][17]

二项分布的累积分布函数和尾概率可以用正则化不完全贝塔函数表示为

${\displaystyle \Pr(X\leq k)=I_{1-p}(n-\lfloor k\rfloor ,\lfloor k\rfloor +1),}$

${\displaystyle \Pr(X\geq k)=I_{p}(\lceil k\rceil ,n-\lceil k\rceil +1).}$^[18]

二项分布的${\displaystyle \,r\,}$阶原点矩满足

${\displaystyle \mu '_{r}=E[X^{r}]=\sum _{j=0}^{r}{\frac {S(r,j)n!p^{j}}{(n-j)!}},}$

其中${\displaystyle \,S(r,j)\,}$表示第二类（英语：Stirling numbers of the second kind）斯特林数。具体而言，

${\displaystyle \mu '_{1}=np,}$

${\displaystyle \mu '_{2}=np+n(n-1)p^{2},}$

${\displaystyle \mu '_{3}=np+3n(n-1)p^{2}+n(n-1)(n-2)p^{3},}$

${\displaystyle \mu '_{4}=np+7n(n-1)p^{2}+6n(n-1)(n-2)p^{3}+n(n-1)(n-2)(n-3)p^{4}.}$

其低阶中心矩为

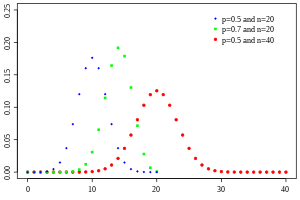
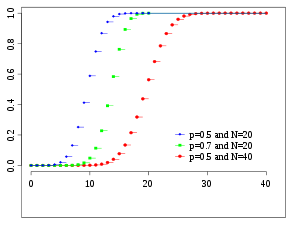
${\displaystyle \mu _{2}=np(1-p),}$

${\displaystyle \mu _{3}=np(1-p)(1-2p),}$

${\displaystyle \mu _{4}=3[np(1-p)]^{2}+np(1-p)[1-6p(1-p)].}$^[19]

标准二项分布

${\displaystyle X'={\frac {X-np}{\sqrt {np(1-p)}}}}$

在${\displaystyle \,n\to \infty \,}$时趋近于标准正态分布。这一结果称作棣莫弗-拉普拉斯定理（英语：De Moivre–Laplace theorem），为中心极限定理的特殊形式。基于这一定理可以得到

${\displaystyle \Pr(\alpha <{\frac {X-np}{\sqrt {np(1-p)}}}<\beta )\to \Phi (\beta )-\Phi (\alpha ),}$

其中${\displaystyle \,\Phi \,}$为标准正态分布的累积分布函数。^[20]

正态分布为连续概率分布，在近似二项分布这类离散概率分布时，可将端点向外偏移${\displaystyle \,0.5\,}$得到

${\displaystyle \Pr(X\leq k)\approx \Phi \left({\frac {k+0.5-np}{\sqrt {np(1-p)}}}\right),}$

从而提升近似的准确性，这种技巧称作连续性校正（英语：Continuity correction）^[21]。何时能采用这一近似依赖于使用经验法则，例如要求${\displaystyle \,np(1-p)>9\,}$，或是在${\displaystyle \,p\leq 0.5\,}$时要求${\displaystyle \,np>5\,}$、在${\displaystyle \,p>0.5\,}$时要求${\displaystyle \,n(1-p)>5\,}$。^[22][23]

当${\displaystyle \,n\to \infty ,p\to 0\,}$，而${\displaystyle \,np\,}$保持不变时，二项分布趋近于参数为${\displaystyle \,np\,}$的泊松分布。以此为基础可以得到

${\displaystyle \Pr(X\leq k)\approx e^{-np}\sum _{j=0}^{k}{\frac {(np)^{j}}{j!}}.}$^[24]

二项分布与其泊松近似之间的绝对误差存在上界。若随机变量${\displaystyle \,X\,}$服从参数为${\displaystyle \,n,p\,}$的二项分布，随机变量${\displaystyle \,Y\,}$服从参数为${\displaystyle \,np\,}$的泊松分布，则

${\displaystyle \sum _{k=0}^{\infty }\|\Pr(X=k)-\Pr(Y=k)\|\leq \min\{2np^{2},3p\}.}$^[25]

通常参数${\displaystyle \,n\,}$为已知。假设随机变量${\displaystyle \,X\,}$服从二项分布，其参数${\displaystyle \,p\,}$未知。若观测到${\displaystyle \,X\,}$的值为${\displaystyle \,x\,}$，采用矩估计和最大似然估计对参数${\displaystyle \,p\,}$的估计量均为${\displaystyle \,{\frac {x}{n}}\,}$，这一估计量为无偏的。^[26]

参数${\displaystyle \,p\,}$的贝叶斯估计量（英语：Bayes estimator）取决于使用的先验分布。若使用连续型均匀分布作为先验分布，即假设${\displaystyle \,0\,}$和${\displaystyle \,1\,}$之间任意等长的区间包含${\displaystyle \,p\,}$的概率都相同，则后验均值估计量为

${\displaystyle {\widehat {p}}={\frac {x+1}{n+2}}.}$

这被称作拉普拉斯–贝叶斯估计量（英语：Laplace–Bayes estimator），曾被皮埃尔-西蒙·拉普拉斯用于估计在太阳连续升起${\displaystyle \,n\,}$天之后，太阳明天还会升起的概率。由于人类知道太阳在过去五千年，即1,826,213天都正常升起，拉普拉斯愿意以1,826,214比1的赔率赌太阳明天继续升起。^[27]

若使用参数为${\displaystyle \,\alpha ,\beta \,}$的贝塔分布作为先验分布，则后验均值估计量为

${\displaystyle {\widehat {p}}={\frac {\alpha +x+1}{\alpha +\beta +n+2}}.}$

采用贝塔分布作为先验分布时，后验分布亦是贝塔分布，即贝塔分布为二项分布的共轭先验。^[28]

若要对参数${\displaystyle \,p\,}$以区间形式给出估计，通过求解

${\displaystyle \sum _{j=x}^{n}{n \choose j}p_{L}^{j}(1-p_{L})^{n-j}={\frac {\alpha }{2}},}$

${\displaystyle \sum _{j=0}^{x}{n \choose j}p_{U}^{j}(1-p_{U})^{n-j}={\frac {\alpha }{2}},}$

所得的区间${\displaystyle \,(p_{L},p_{U})\,}$为一个置信水平近似为${\displaystyle \,1-\alpha \,}$的置信区间，称作克洛珀-皮尔逊区间（Clopper-Pearson interval）。^[29]

正态分布可以用于推导近似的置信区间。若用${\displaystyle \,\lambda _{\alpha /2}\,}$表示标准正态分布的第${\displaystyle \,1-{\frac {\alpha }{2}}\,}$分位数，即${\displaystyle \,\Phi (\lambda _{\alpha /2})=1-{\frac {\alpha }{2}}\,}$，则区间两端的近似值为

${\displaystyle {\frac {x}{n}}\pm {\frac {\lambda _{\alpha /2}}{\sqrt {n}}}{\sqrt {{\frac {x}{n}}\left(1-{\frac {x}{n}}\right)}}.}$^[30][31]

• 概率论
• 機率分布
• 正态分布
• 卜瓦松分布
• 伯努利分布
• 负二项分布
• 多项分布（英语：Multinomial distribution）