Ennéadécagone — Wikipédia
Un ennéadécagone ou ennéakaidécagone est un polygone à 19 sommets, donc 19 côtés et 152 diagonales.
La somme des angles internes d'un ennéadécagone non croisé vaut 3 060 degrés.
Ennéadécagones réguliers
[modifier | modifier le code]Un ennéadécagone régulier comprend 19 côtés de même longueur et 19 angles internes de même mesure. Il y a neuf ennéadécagones réguliers : huit étoilés (les ennéadécagrammes notés {19/k} pour k de 2 à 9) et un convexe (noté {19}). C'est de ce dernier qu'il s'agit lorsqu'on parle de « l'ennéadécagone régulier ».
- Les huit ennéadécagones réguliers étoilés
- {19/2}
- {19/3}
- {19/4}
- {19/5}
- {19/6}
- {19/7}
- {19/8}
- {19/9}
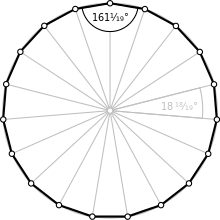
Caractéristiques de l'ennéadécagone régulier
[modifier | modifier le code]Chacun des 19 angles au centre mesure et chaque angle interne mesure .
Si a est la longueur d'une arête :


 French
French Deutsch
Deutsch