Função gama – Wikipédia, a enciclopédia livre

Esta página cita fontes, mas que não cobrem todo o conteúdo. Ajude a inserir referências (Encontre fontes: ABW  • CAPES  • Google (N • L • A)). (Maio de 2012)

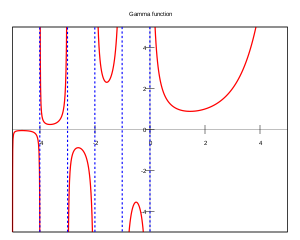
Em matemática, a função gama (representada pela letra maiúscula grega ${\displaystyle \Gamma }$) é uma extensão da função factorial para o conjunto dos números reais e complexos, com o argumento subtraído em 1. Se n é um inteiro positivo define-se da seguinte forma:

${\displaystyle \Gamma (n+1)=n!}$ ou ${\displaystyle \Gamma (n)=(n-1)!}$

Esta função é estendida por uma continuação analítica (ou extensão analítica) para todos números complexos com, não estando definida apenas nos inteiros não-positivos (em que a função tem polos simples). Portanto, para números complexos com a parte real positiva a definição segue por uma integral imprópria convergente:

${\displaystyle \Gamma (t)=\int _{0}^{\infty }x^{t-1}e^{-x}dx}$

Podemos encontrar a demonstração da convergência desta integral no artigo de Emil Artin, The Gamma Function.

A função gama é debutante em diversas funções de distribuição probabilísticas, sendo assim encontra aplicações nos campos da probabilidade, estatística e combinatória.

A função gama pode ser vista como solução do seguinte problema de interpolação:

"Encontrar uma curva suave que conecta os pontos (x , y) dados por y = (x − 1)! em que x é um inteiro positivo."

Esboçando em um gráfico os primeiros números fatoriais fica claro que a curva pode ser desenhada, mas seria preferível ter um expressão analítica que descreve precisamente a curva, na qual o número de operações não dependa do tamanho  de x. A simples fórmula recursiva para o fatorial x! = x × ... × 2 × 1,  não pode ser usada para obter valores fracionários, pois é válida apenas quando x é um número natural. No entanto, foi demonstrado por Euler que não há uma expressão analítica convencional para fatorial, no sentido que não pode ser a combinação finita (com um número finito de termos) de somas, potências, produtos, funções exponenciais e logaritmos, demonstrado em seu artigo intitulado "Sobre progressões transcendentais, nas quais o termo geral não pode ser expresso algebricamente", ("De progressionibus transcendentibus seu quarum termini generales algebraice dari nequeunt"). A função gama é uma solução que não só resolve este problema, mas também possuí distinguíveis propriedades entre as candidatas, como é mostrado no Teorema de Bohr-Mollerup.

É fácil perceber, através da regra da cadeia e de recursos da integração imprópria, que

${\displaystyle \int _{0}^{\infty }e^{-r}\,dr=\left.-e^{-r}\right\vert _{0}^{\infty }=1}$

Usando o método da substituição, de modo que ${\displaystyle r=st,dr=tds}$, (t>0 e fixo), obtém-se:

${\displaystyle \int _{0}^{\infty }e^{-st}\,ds={\frac {1}{t}},t>0}$

Derivando-se em relação a ${\displaystyle t}$ e aplicando a fórmula de Leibniz:

${\displaystyle \int _{0}^{\infty }se^{-st}\,ds={\frac {1}{t^{2}}},t>0}$

Utilizando o mesmo processo novamente:

${\displaystyle \int _{0}^{\infty }s^{2}e^{-st}\,ds={\frac {1.2}{t^{3}}},t>0}$

Derivando sucessivas vezes em relação a ${\displaystyle t}$:

${\displaystyle \int _{0}^{\infty }s^{n}e^{-st}\,ds={\frac {n!}{t^{n+1}}},t>0}$

Para ${\displaystyle t=1}$

${\displaystyle \int _{0}^{\infty }s^{n}e^{-s}\,ds=n!}$

Dessa forma, tem-se uma função fatorial definida para quaisquer valores reais positivos ${\displaystyle x}$, de modo que:

${\displaystyle g(x)=\int _{0}^{\infty }e^{-s}s^{x}\,ds=x!}$

Contudo, consagrou-se o uso de uma definição levemente destoante, a Função Gama de Euler, tal que

${\displaystyle \Gamma (x)=\int _{0}^{\infty }e^{-t}t^{x-1}\,dt}$

Assim,

${\displaystyle \Gamma (x)=g(x-1)}$

E, analogamente, para números inteiros,

${\displaystyle \Gamma (n)=(n-1)!}$

Com isso, acabamos de provar que a função gama funciona como uma representação do Fatorial, quando é aplicada em números inteiros, isso permite a idealização de afirmarmos que quando calculamos a função gama para outros números em seu domínio (Números fracionários ou irracionais) estamos obtendo o "fatorial" desses números. Um exemplo disso, é a seguinte relação, da qual omitiremos a demonstração:

${\displaystyle (1/2)!=\Gamma \left({\frac {3}{2}}\right)={\frac {1}{2}}\Gamma \left({\frac {1}{2}}\right)={\frac {1}{2}}{\sqrt {\pi }}}$

A função gama incompleta é obtida pela mesma integral que a função gama, porém com uma integral indefinida no lugar da integral definida:

${\displaystyle \Gamma (a,x)=\int _{x}^{\infty }t^{a-1}\,e^{-t}\,dt.}$

${\displaystyle \gamma (a,x)=\int _{0}^{x}t^{a-1}\,e^{-t}\,dt.}$

A função digama é a derivada do logaritmo da função gama:

${\displaystyle \psi (x)={\frac {d}{dx}}\ln {\Gamma (x)}={\frac {\Gamma '(x)}{\Gamma (x)}}.}$

A função beta, também chamada de Integral de Euler de primeiro tipo, pode ser definida por uma razão de funções gama:

${\displaystyle \mathrm {B} (x,y)={\frac {\Gamma (x)\Gamma (y)}{\Gamma (x+y)}}}$

A propriedade mais importante da função gama é dada por

${\displaystyle \Gamma (z+1)=z\Gamma (z)}$

Que pode ser obtida pela integração por partes da definição da função gama

${\displaystyle \Gamma (z+1)=\left.-e^{-t}t^{z}\right\vert _{0}^{\infty }+z\int _{0}^{\infty }t^{z-1}e^{-t}dt}$

O lado esquerdo do resultado é igual a zero. A integral do lado direito do resultado é a própria definição da função gama.

Segue desta propriedade que

${\displaystyle \Gamma (z)=(z-1)\Gamma (z-1)}$

E também

${\displaystyle \Gamma (z+1)=z(z-1)(z-2)...}$

Para números inteiros, a recursividade da propriedade cai na definição do fatorial. Esta propriedade é válida também para números no domínio dos complexos.

Além delas, existe a importante propriedade abaixo encontrada por Hamilton Brito de forma independente, com ${\displaystyle a}$ e ${\displaystyle b}$ ${\displaystyle \in \mathbb {N} }$ sendo ${\displaystyle a\geq 2}$ e ${\displaystyle b\geq 1}$:

${\displaystyle \Gamma (a+bi)\cdot \Gamma (a-bi)=b\cdot (b^{2}+1)\cdot \pi \cdot cossech(b\cdot \pi )\prod _{n=2}^{a-1}(b^{2}+n^{2})}$

A função gama pode ser escrita por um produto de Hadamard:

${\displaystyle \Gamma (z)={\frac {e^{-\gamma z}}{z}}\prod _{n=1}^{\infty }\left(1+{\frac {z}{n}}\right)^{-1}e^{\frac {z}{n}}}$

A integral que define a função gama converge para todo

${\displaystyle x>0}$

Assim um intervalo de definição da função é:

${\displaystyle \Gamma (x):(0,{\infty })}$

Prova

Escrevendo A função como:

${\displaystyle \int _{0}^{1}t^{x-1}e^{-t}dt+\int _{1}^{\infty }t^{x-1}e^{-t}dt}$

A segunda integral converge muito rápido pelo fator ${\displaystyle e^{-t}}$ que tende a zero quando ${\displaystyle t}$ tende a infinito, neutralizando qualquer crescimento que o termo ${\displaystyle t^{x-1}}$ apresente.

Na primeira integral para ${\displaystyle 0<t<1}$ a função ${\displaystyle e^{-t}}$ fica controlada. Logo a convergência dessa integral vai depender apenas do termo ${\displaystyle t^{x-1}}$.

Para ${\displaystyle x>0}$

${\displaystyle \int _{0}^{1}t^{x-1}dt={\frac {1^{x}}{x}}-0={\frac {1}{x}}<{\infty }}$

Para ${\displaystyle x=0}$

${\displaystyle \int _{0}^{1}t^{-1}dt=ln{1}-ln{0}={\infty }}$

Para ${\displaystyle x<0}$ temos que ${\displaystyle x-1<-1}$, então:

${\displaystyle \int _{0}^{1}t^{x-1}dt>\int _{0}^{1}t^{-1}dt={\infty }}$

Pela propriedade fundamental, pode-se estender o domínio da função gama em intervalos que contém números negativos. Define-se então que

${\displaystyle \Gamma (z)={\frac {\Gamma (z+1)}{z}}}$

Para números no intervalo z ∈ (-1, 0), como z < 0, vê-se que

${\displaystyle \Gamma (z)<0}$

E também que

${\displaystyle \lim _{z\to 0^{-}}\Gamma (z)=\lim _{z\to 1^{+}}\Gamma (z)=-\infty }$

Continuando com o mesmo processo, o domínio da função gama passa a ser

${\displaystyle \mathbb {R} \,}$ - {0, -1, -2, -3, ...}

Um resultado de interesse em algumas aplicações calculado pela Função é ${\displaystyle \Gamma \left({\frac {1}{2}}\right)={\sqrt {\pi }}}$

Demonstração

${\displaystyle \Gamma \left({\frac {1}{2}}\right)=\int _{0}^{\infty }t^{-\left({\frac {1}{2}}\right)}e^{-t}dt}$

Fazendo ${\displaystyle t=r^{2}}$, obtemos ${\displaystyle dt=2rdr}$ logo:

${\displaystyle \int _{0}^{\infty }t^{-\left({\frac {1}{2}}\right)}e^{-t}dt=2\int _{0}^{\infty }e^{-r^{2}}dr}$

Utilizando a técnica de Liouville:

${\displaystyle I=\int _{0}^{\infty }e^{-x^{2}}dx}$

${\displaystyle I^{2}=\int _{0}^{\infty }e^{-x^{2}}dx\int _{0}^{\infty }e^{-y^{2}}dy=\int _{0}^{\infty }\int _{0}^{\infty }e^{-(x^{2}+y^{2})}dxdy}$

A última integral é uma integral dupla facilmente calculada em coordenadas polares:

${\displaystyle I^{2}=\int _{0}^{\frac {\pi }{2}}\int _{0}^{\infty }e^{-r^{2}}rdrd{\theta }={\frac {\pi }{4}}}$

Utilizando uma troca de variáveis é fácil chegar ao resultado.

${\displaystyle I^{2}={\frac {\pi }{4}}}$

${\displaystyle I={\frac {\sqrt {\pi }}{2}}}$

${\displaystyle 2\int _{0}^{\infty }e^{-r^{2}}dr=2{\frac {\sqrt {\pi }}{2}}={\sqrt {\pi }}}$

Sendo assim:

${\displaystyle \Gamma \left({\frac {1}{2}}\right)={\sqrt {\pi }}}$

Referências

• Boyce e DiPrima. Equações Diferenciais Elementares e Problemas de Valores de Contorno, editora LTC, 9ª edição, 2010.
• Dennis G. Zill, Michael R. Cullen; Equações Diferenciais, vol 1; Editora Makron Books do Brasil
• Davis, Philip J.; Abramowitz, Milton; Stegun, Irene. Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables. 1972.

• «Calculadora - Função gama»